- Где использовать математический аппарат в планировании внутрицехового производства в ERP?
- Упрощённая схема производства
- Реализация внутрицеховых операций в 1С:ERP
- Оптимизация производственного расписания
- Параметризация и целевые функции для составления расписаний
- Применяем математический аппарат к тестовой постановке задачи
- Оценка сложности задачи составления расписаний
- Связывание задачи с функционалом 1С:ERP и предметной областью
- Барабан-Буфер-Веревка в 1С:ERP
- Подбираем альтернативные пути решения задач Теории расписаний
- Когда переход с допустимого на оптимальное расписание производства оправдан?
Где использовать математический аппарат в планировании внутрицехового производства в ERP?
Упрощённая схема производства
Давайте начнем с неакадемической стороны задачи управления производственными операциями и процессами.
Что такое планирование производства? В общем это что, на каком оборудовании должно быть сделано, чтобы успеть в срок и не затоварить склады. К сожалению, случается так, что специалисты по производственной логистике не видят в задаче планирования постановку одной из сложнейших задач математической оптимизации, которая относится к теории исследования операций и теории расписания.
В первую очередь давайте познакомимся с некоторыми терминами, которые помогут нам в дальнейшем и сделаем это на основе небольшого реального примера, которому мы и будем следовать в протяжении всего разговора.
На рисунке 1 показана упрощенная схема производства косметического крема. Многокомпонентный боксик, состоящий из названия рабочего центра, производимой продукции, элементарной операции и ее продолжительности, представляет собой описание производственной операции (далее операция).
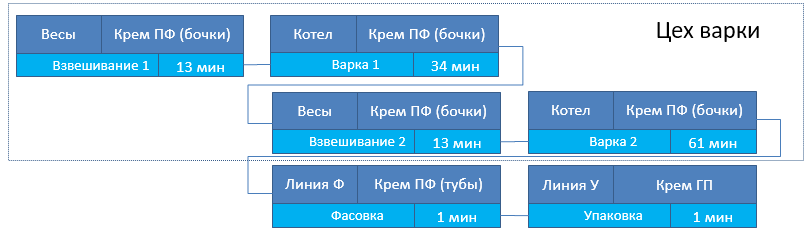
Рисунок 1. Схема производства крема
Для каждой операции важно:
- Какой Продукт производится. Например, на первой операции это «Крем ПФ (бочки)». Далее понятие продукта мы обобщим и будем использовать термин «Задание» вследствие того, что в англоязычной литературе для его описания применяется термин «Job».
- На каком рабочем центре (далее РЦ, что совпадает с термином в рамках 1С:ERP) идет производство.
- Продолжительность операции.
Для простоты понимания на схеме не указаны несколько важных параметров, которые также используются для расчета расписания:
- Материальный состав продукта для решения задачи обеспечения.
- Время переналадки РЦ.
- Предельная Загрузка РЦ для учета ограничения производственной мощности сверху для параллельных РЦ.
- Исполнитель: сотрудник с необходимой специализацией и уровнем профессионализма.
Реализация внутрицеховых операций в 1С:ERP
В 1С:ERP до версии 2.5.7 для описания производственных операций внутри цеха используется табличная часть «Операции» справочника «Маршрутные карты», который для нашей схемы показан на рисунке 2. Стоить заметить, что начиная с версии 2.5.7 справочник «Маршрутные карты» были объединен со справочником «Спецификации».
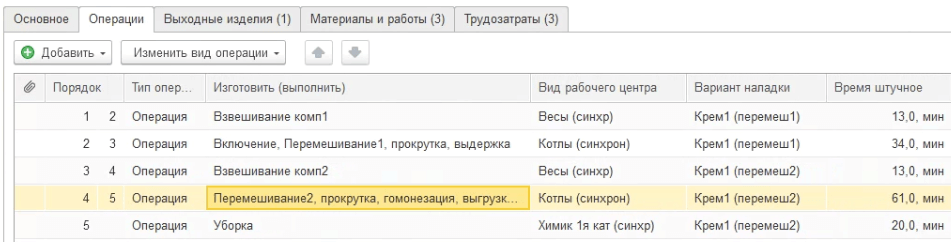
Рисунок 2. Операции маршрутной карты
Перед тем как продолжить, также следует уточнить, что же является Заданием в терминах 1С:ERP. Одним из самых важных параметров для заказчика является дата отгрузки. Поэтому базовым объектом для Задания в общем случае является «Заказ покупателя», в котором и определяется продукт, количество и календарная дата отгрузки.
Однако, производственные компании часто объединяют множество заказов клиента в один заказ на производство, исходя их двух критериев: размера партии запуска и даты отгрузки. Поэтому более предпочтительной основой для Задания в 1С:ERP является «Заказ на производство». Пример Производственного Заказа указан на рисунке 3.
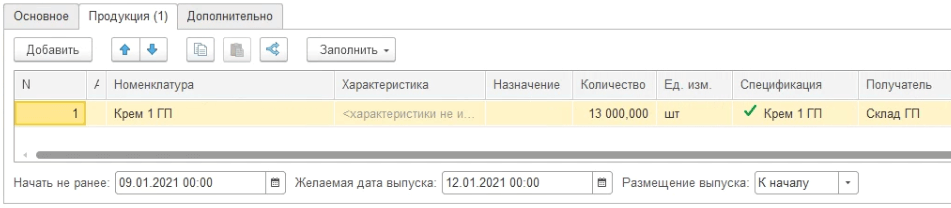
Рисунок 3. Заказ на производство
Но одного Производственного Заказа недостаточно для определения Задания, т. к. в процессе производства желательно выпускать передаточными Партиями, которые в общем случае зависят от мощности РЦ.
В 1С:ERP Передаточная партия называется Оптимальным запуском и определяется в Ресурсной спецификации:
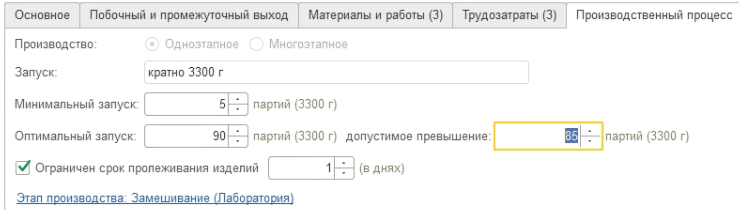
Рисунок 4. Параметры запуска в производство
Примечание: Передаточная партия в нашем примере равна 90 штукам, т. к. объем одного котла 30 литров, вместимость одной коробки 60 тюб., масса крема в тюбике 55 грамм., тогда 9 кор в одном котле = 30 / (60 × 0,055). Смена 24 ч. (пример модельный), 2 Котла, тогда доступного времени 2880 мин. Продолжительность операции 285 мин., тогда можно приготовить 10 котлов, по 9 коробок, т. е. 90 штук за сутки.
Исходя из данного параметра, 1С:ERP делит «Заказ на производство» на множество Партий запуска именуемых «Этапами на производство». Следовательно «Этап на производство» вместе с Выпускаемой номенклатурой и количеством далее в статье и будет называться Заданием.
Немного подрезюмируем. Начали с того, что под Заданием можно понимать Заказ клиента, далее договорились, что они объединяются в Заказы на производство, а далее увидели, что Заказы на производство разбиваются на Этапы и в конечном итоге объектной сущностью, которая и будет подвергаться комбинаторным манипуляциям для расписания станет Этап.
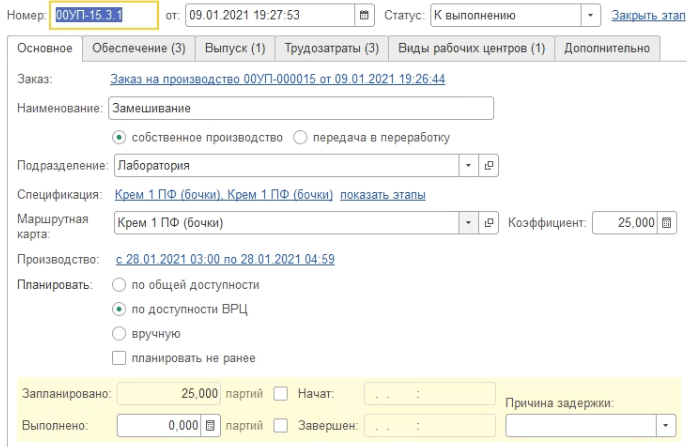

Рисунок 5. Этап производства
Второй важный вопрос, который следует обсудить перед переходом к математической постановке задачи это РЦ.
Существует три важных параметра любого РЦ:
- параллельность (допускается / не допускается);
- загрузка (единичная / синхронная / асинхронная);
- переналадка.
Параллельные рабочие центры — набор однотипного оборудования, способный выполнить одну и ту же операцию. В нашем примере Весов в лаборатории может быть множество и все они выполняют функцию Взвешивания. Однако в общем случае все может быть намного сложнее — весы в Разных Лабораториях (Цехах) являются Параллельными, но с меньшим приоритетом. Также производительность РЦ при выполнении одной и той же Операции может быть сильно различной.
Например, обычный токарный станок и с ЧПУ. Параллельность в 1С:ERP определяется понятием Вид рабочего центра, в который может входить несколько РЦ.

Рисунок 6. Виды рабочих центров
Загрузка в свою очередь может быть:
- единичной,
- синхронной,
- асинхронной.
При синхронной загрузке Задания в РЦ обрабатываются одинаковое время при этом старт работ и окончание одинаковое для всех Продуктов, которые находятся в РЦ. В нашем примере это Котлы. В котле могут одновременно вариться различные партии одной номенклатуры.
В случае асинхронной загрузки Задания в РЦ могут обрабатываться различное время, а старт работ и окончание независимы для партии продукта. Например, это может быть Печь с независимой загрузкой, когда температура поддерживается постоянной и не зависит от Продукта.
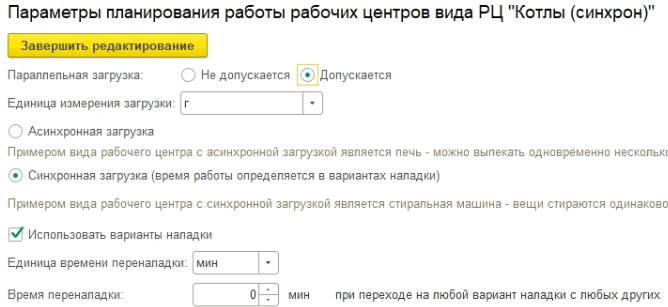
Рисунок 7. Параметры загрузки ВРЦ
Переналадка — один из основных видов Потерь производительности оборудования. В нашем примере, если после варки «Крема 1», в том же Котле требуется запустить варку «Крема 2», необходимо тщательно очистить котёл. В общем случае Переналадка может включать в себя Замену технологического инструмента, оснастки, смену рабочей температуры и т. п. Время наладки в 1С:ERP определяется понятием Вариантов наладки.
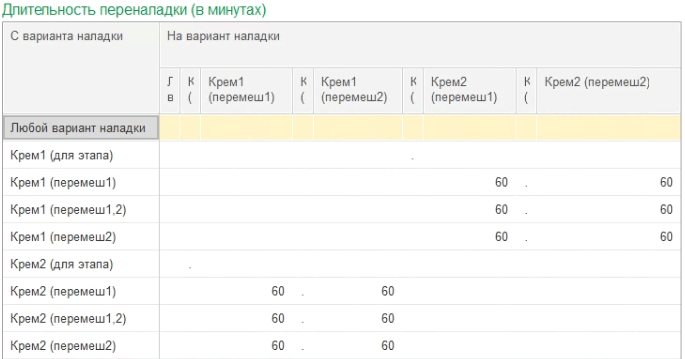
Рисунок 8. Длительность переналадки
Осталось отметить еще один немаловажный момент при составлении Производственного расписания — доступность материалов. Никакой Продукт нельзя выпустить, без сопутствующих затрат Материалов, однако их остатки на Предприятии в процессе производства и снабжения — постоянно изменяющаяся величина, которую необходимо учитывать в процессе планирования производства.
В 1С:ERP для определения ограничений в доступности материалов для каждой производственной партии используется вкладка Обеспечение в Этапе на производство.
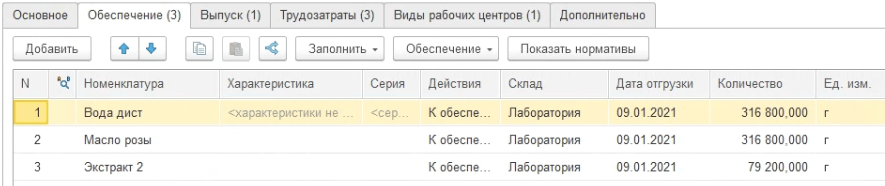
Рисунок 9. Обеспечение Этапа материалами
Оптимизация производственного расписания
Подводя итоги, задачей производственного планирования является составление расписания, целью которого является разместить каждое Задание на РЦ так, чтобы выполнялась технологическая последовательность работ, выполнялись бы ограничения по материалам и продукт в конечном счете был выпущен в полном объеме и в необходимый срок.
Для того чтобы ввести понятие оптимальности Расписания нужно определить дополнительные задачи, которые должен решать специалист по Планированию в процессе своей работы:
- Выпустить «Точно в срок» принимая риск возможной недозагрузки оборудования или «Как можно раньше» принимая риск роста незавершенного производства (НЗП).
- Максимизировать загрузку оборудования или равномерно его загрузить.
- Минимизировать НЗП, запустив Задание без временного буфера или снизить риски минимизируя штрафы за недопоставку, запуская Задание пораньше.
К сожалению, многие из этих требований противоречивы и вручную найти оптимальное расписание с учетом всех потребностей бизнеса и множества ограничений представляется невозможным, поэтому в большинстве случаев специалисты по Планированию строят первое возможное допустимое расписание и задают его в производство.
Насколько подобный подход оптимален? Давайте попробуем ответить на этот вопрос на нашем примере.
Таблица 1 содержит простую задачу составления расписания для нашего примера.
Таблица 1. Матрица времени выполнения заданий на РЦ
| Задания | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| РЦ | 1 | 78 | 78 | 78 | 78 |
| 2 | 285 | 285 | 285 | 285 | |
| 3 | 20 | 0 | 20 | 0 | |
| 4 | 0 | 60 | 0 | 60 | |
Нам дана матрица 4×4, в которой:
- По строкам стоят рабочие центры (1 — весы, 2 — котел, 3 — фасовка , 4 — упаковка).
- По столбцам Задания (Этап 1 + Крем 1; Этап 2 + Крем 2; Этап 3 + Крем 1; Этап 4 + Крем 2). Здесь задание следует читать так: «Этап 1 + Крем» означает, что в рамках Этапа 1 будет производиться Крем 1.
- На пересечении операционное время на каждом РЦ для каждого задания в минутах.
Будем считать, что каждый РЦ дан нам в двойном экземпляре.
Таблица 2 в свою очередь представляет собой матрицу переналадки, т. е. при подаче на один котел Крема 1 и Крема 2 необходима очистка, которая занимает 60 минут.
Таблица 2. Матрица переналадок
| Задания | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Задания | 1 | 0 | 60 | 0 | 60 |
| 2 | 60 | 0 | 60 | 0 | |
| 3 | 0 | 60 | 0 | 60 | |
| 4 | 60 | 0 | 60 | 0 | |
В начале рассмотрим несколько неперестановочных расписаний.
Неперестановочное расписание — это вид расписания, когда последовательность задачи Заданий на каждый РЦ одинакова.
Тогда описание расписания можно задать простым вектором, например, S1 = (1, 2, 3, 4).
Для такого расписания распределение по РЦ в представлении Диаграммы Ганта будет выглядеть:

Рисунок 10. Диаграмма Ганта для расписания (1, 2, 3, 4)
Для расписания S2 = (1, 3, 2, 4) Диаграмма Ганта будет выглядеть:

Рисунок 11. Диаграмма Ганта для расписания (1, 3, 2, 4)
Видно, что в этом случае возникает переналадка.
Для расписания S3 = (4, 2, 3, 1) Диаграммы Ганта будет выглядеть:

Рисунок 12. Диаграмма Ганта для расписания (4, 2, 3, 1)
Видно, что в этом случае также возникает переналадка.
Для более полного примера рассмотрим дополнительно перестановочное расписание.
Перестановочное расписание — это вид расписания, когда последовательность задачи Заданий на каждый РЦ может быть различной.
Тогда описание расписания можно задать более сложным вектором, например,
S4 = (2, 1, 4, 3; 2, 1, 4, 3; 2, 1, 4, 3; 2, 1, 4, 3).

Рисунок 13. Диаграмма Ганта для расписания (2, 1, 4, 3, 2, 1, 4, 3, 2, 1, 4, 3, 2, 1, 4, 3,)
Каждое из 4-х расписаний допустимо, но имеет различное время окончания (далее Сmax).
Таблица 3. Время окончания заданий
| Расписание | Сmax |
|---|---|
| 1 | 708 |
| 2 | 768 |
| 3 | 728 |
| 4 | 708 |
Первая проблема такого подхода состоит в том, что только не перестановочных расписаний можно составить 4! = 16.
Здесь важен факториал числа, означающий сверхбыстрый рост количества расписаний при росте числа под факториалом. Количество перестановочных расписаний 4*4! = 64. Конечно не все этапы могут быть переставлены, так как есть условия технологического цикла.
Вторая проблема состоит в том, что мы пока не ввели в этой задаче «Необходимую дату отгрузки» (далее dj).
Таблица 4 содержит этот параметр и дополнительно рассчитано суммарное время запаздывания заданий (далее Tij = max{0, Сj − dj})
Таблица 4. Необходимая дата отгрузки и суммарное время запаздывания заданий
| Расписание | Необходимая дата отгрузки Заданий (по порядку) | Время окончания заданий (по порядку) | Суммарное время запаздывания заданий |
|---|---|---|---|
| 1 | 700,700,300,300 | 383,423,668,708 | 0 + 0 + (668 − 300) + (708 − 300) = 776 |
| 2 | 700,700,300,300 | 383,768,383,768 | 0 + (768 - 700) + (383 − 300) + (768 − 300) = 619 |
| 3 | 700,700,300,300 | 728,423,728,423 | (728 − 700) + 0 + (728 − 300) + (423 − 300) = 579 |
| 4 | 700,700,300,300 | 383,423,668,708 | 776 |
Запаздывающие задания приводят к штрафам за недопоставку, следовательно Расписания 1 и 3 не оптимальны с точки зрения этого критерия, хотя они оптимальны с точки зрения максимального времени окончания работ, что соответствует максимизации загрузки оборудования.
Параметризация и целевые функции для составления расписаний
Теперь, когда мы ввели все необходимые термины, а также рассказали какие объекты 1С:ERP используются для решения задачи составления оптимального расписания, дадим более формальное математическое определение этой задачи.
Начнем с того, что раздел исследования операций, в котором строятся и анализируются математические модели календарного планирования, то есть упорядочивание во времени различных целенаправленных действий с учетом целевой функции и различных ограничений называется Теория расписаний (далее ТР).
В 1979 г Грэхам, Лаулер, Ленстра и Кан для задач теории расписаний ввели следующие обозначения:
α|β|γ
Набор параметров α содержит характеристики задачи, связанные с типами РЦ, если α равно:
- 1 — задача для одного рабочего центра (далее РЦ). Например конвейер или роботизированная производственная линия без разрывов.
- Pm — идентичные параллельные РЦ когда вместо одного прибора доступно m РЦ — M1, M2, … Mm с одинаковой производительностью. Например, группа однотипных станков.
- Qm — параллельные приборы с различной производительностью.
Мы будем говорить о задачах цеха (Shop-scheduling), когда каждое задание состоит из операций, выполнение которых может назначаться на определенные РЦ внутри цеха. В общем случае дано m приборов и каждое задание j содержит операции O1, j, ..., Onj, j. Между операциями могут быть заданы отношения предшествования, то есть маршрут обработки. В общем случае задание может посещать РЦ несколько раз. Время выполнения операции Oij равно pij.
Для описания маршрутизации приняты следующие обозначения:
- Jm — системы типа Job-shop — заданы отношения предшествования между операциями для одного задания, при этом нет предшествований между отдельными заданиями. Количество операций разных заданий при этом может быть различным.
- Fm — системы типа Flow-shop — каждое задание состоит из одних и тех же операций, т. е. nj равно m. Так же i-я операция каждой работы выполняется на одном и том же приборе Mi.
- Om — системы типа Open-shop — аналогично Flow-shop однако без отношения предшествования между операциями.
В наборе параметров β уточняются характеристики задачи и ограничения на составление расписания.
Если β равно:
- rj — моменты поступления заданий на обслуживание («начать не ранее», см. рис. 3);
- dj — предельные сроки завершения обслуживания («желаемая дата выпуска», см. рис. 3);
- sj — время переналадки: может быть зависимым от последовательности заданий (job‑dependent) и независимым;
- perm(permutation) — допустимы перестановки работ, т. е. последовательность Заданий на каждом РЦ может быть различной;
- pmnt, preem — допустимы прерывания;
- batch — задания обслуживаются партиями;
- re-entrant — задания могут обрабатываться на одном приборе несколько раз.
Перед тем как перейти к описанию γ, опишем типы наиболее часто применяемых штрафных функций:
- Cj — момент окончания обслуживания задания j.
- Lj — временное смещение, равное Сj − dj.
- Tj — запаздывание, равное max{0, Сj − dj}.
- Ej — опережение, равное max{0, dj − Cj}.
- Uj — задание запаздывает, равно 0, если Cj ≤ dj, и 1, в противном случае.
В наборе параметров γ указывается целевая функция, ниже приведены примеры наиболее применяемых целевых функций:
- Сmax — минимизация максимального времени окончания заданий (соответствует задаче максимизации загрузки оборудования). В нашем примере мы будем ориентироваться именно на эту целевую функцию.
- Lmax — минимизация максимального временного смещения (соответствует задаче выпуска «точно в срок»). Далеко не всегда оптимизация Сmax ведет к оптимизации Lmax. Представьте себе, что вы действительно смогли выпустить 20.03.2021 и это соответствует минимизации срока выпуска, а надо по заказу к 25.03.2021 и каждый день пролеживания продукции на складе будет вам стоить денег.
- ∑j∈NCj — минимизация суммарного времени окончания обслуживания заданий (соответствует задаче минимизации НЗП).
- ∑j∈NTj — минимизация суммарного времени запаздывания (минимизация штрафов за недопоставку).
Следует отметить, что целевые функции могут быть композитными, т. е. включать в себя различные целевые функции.
Применяем математический аппарат к тестовой постановке задачи
Теперь, в качестве примера, запишем в математической постановке нашу тестовую задачу. Напомним, что у нас есть четыре РЦ, при этом согласно маршрутной карте заданы отношения предшествования между операциями для одного задания, при этом нет предшествований между отдельными заданиями. Это значит, что по определению у нас J (Job-shop) 4.
Также у нас встречаются все ограничения:
- на начало работ;
- на завершение работ;
- на переналадку;
- на непрерывность производимых работ, например нельзя, чтобы котел не остывал;
- на объединение партий, например чтобы обеспечить не большее и не меньшее количество возможное на загрузку в РЦ;
- на возможность захода задания на один и тот же РЦ несколько раз.
Целевая функция может быть композитная, включающая максимальный момент завершения заданий и суммарное время запаздывания.
Следовательно общая постановка может иметь вид:
J4 | rj dj sj perm (pmnt) batch re‑entrant | α Cmax + β ∑j∈NTj
Оценка сложности задачи составления расписаний
Вообще говоря, задачи теории расписаний обладают рядом черт, обуславливающих методику их составления и решения.
Во-первых, даже для простых параметрических задач не удается представить решения в виде аналитического выражения от соответствующих параметров, то есть в виде формулы. Поэтому задачи ТР, в подавляющем большинстве, не поддаются аналитическому решению и должны решаться численно.
Во-вторых, большинство задач ТР содержит в своих формулировках большое количество числового материала, не сводящегося к аналитическим выражениям. Поэтому численное решение этих задач, за немногими исключениями, возможно лишь с помощью компьютера. Класс таких задач обычно относят к комбинаторной оптимизации.
Когда мы решаем задачу комбинаторной оптимизации, возникает важный вопрос на сколько сложна или трудоемка задача. В комбинаторной оптимизации задачи условно делятся на:
- полиномиально разрешимые (относительно простые);
- полиномиально проверяемые (сложные);
- полиномиально не проверяемые (очень сложные).
Введем несколько терминов, позволяющих раскрыть эти понятия.
- Размерность задачи (n) — число входящих данных в алгоритм.
- Трудоемкость алгоритма Т(n) — верхняя граница времени работы алгоритма.
- Трудоемкость имеет порядок O(g(n)) если существуют такие константы С и n0, что выполняется условие T(n) ≤ Cg(n) для любого n ≥ n0.
- Если трудоемкость алгоритма имеет порядок O(nk), где k — константа, не зависящая от n, то говорят, что задача полиномиально разрешима. Полиномиально разрешимые задачи относят к классу P.
- NP — класс задач, проверяемых за полиномиальное время.
Логично было бы предположить, что задачи которые не относятся к P относятся к NP однако это не так, более того Задача о равенстве классов P и NP является одной из центральных открытых проблем теории алгоритмов, суть которой сводится к тому, что если пока для задачи не найден полиномиальный алгоритм решения это не значит, что он когда-либо не найдется в будущем.
Как бы то ни было пока научное сообщество склоняется в сторону отрицательного ответа на этот вопрос, в основном, вследствие того, что эффективных полиномиальных алгоритмов решения даже для базовых задач комбинаторной оптимизации (к которым относятся Задача о выполнимости, Задача о разбиении, Задача о ранце, Задача коммивояжера) до сих пор для общих случаев не придумано.
Связывание задачи с функционалом 1С:ERP и предметной областью
Перед тем как перейти к методам решения этой задачи хотелось бы на шаг вернуться к бизнес-процессу планирования производства и его реализации в рамках 1С:ERP. Упрощенно его можно описать рисунком 14.

Рисунок 14. Упрощенная схема бизнес-процесса планирования
На схеме видно, что обычно выделяют три уровня производственного планирования:
- Объемно-календарное (MPS, Master Production Schedule) — определение количественных показателей каждого выпускаемого изделия в привязке к временным отрезкам планирования в пределах всего срока планирования).
- Расписание на уровне предприятия (межцеховое) (APS, Advanced Planning & Scheduling) — построение расписания работы оборудования в рамках всего предприятия. Полученные, таким образом, частные расписания производственных цехов должны быть взаимосвязанными с точки зрения готового изделия и его полного маршрута между цехами.
- Расписание внутрицеховое (ODS, Operational/Detailed Scheduling) — обеспечивает составление производственного расписания с минимальными переналадками оборудования и параллельной работой производственных мощностей для уменьшения времени получения готового продукта и времени простоя.
Функционал планирования производства в 1С:ERP реализован в данной классической схеме. Есть возможность:
- Объемно-календарного планирования с помощью функционала Планов производства, но в рамках этой статьи подробно на нём мы останавливаться не будем.
- Межцехового планирования с помощью функционала Планирования графика производства в интерфейсе Диспетчирования этапов, как это показано на рисунке 15.

Рисунок 15. Форма планирования графика производства Заказа
- Внутрицехового планирования с помощью функционала Пооперационного планирования, как это показано на рисунке 16.
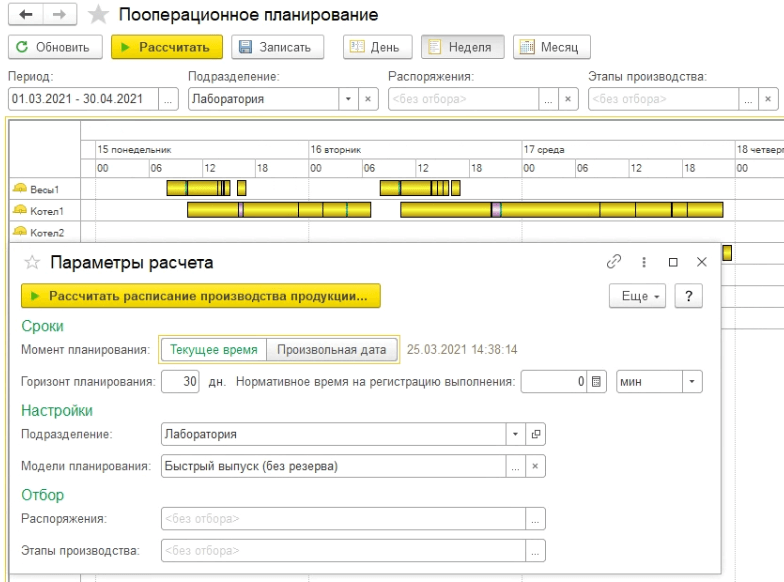
Рисунок 16. Форма пооперационного планирования
Постараемся, не вдаваясь в подробности, пояснить какая же математика кроется внутри 1С:ERP в процессе решения задачи производственного планирования на момент версии 2.5.7.
Барабан-Буфер-Веревка в 1С:ERP
Основная методика решения задачи Планирования производства на уровне Межцехового планирования в 1С:ERP это методика, взятая из Теории ограничений Э. Голдрата и называется она Барабан-Буфер-Веревка.
Основные шаги по использованию методики:
- Выявить РЦ, являющиеся узкими местами. Методика называет эти РЦ барабанами.
- Обеспечить наиболее эффективную загрузку барабанов. Для этого следует точно составить расписание работы этих барабанов, исключающее простои.
- Подчинить выполнение работы на прочих рабочих центрах работе барабана.
- Время производства на рабочих центрах, стоящих в процессе производства перед барабаном, методика называет буфером. Работа в буферах должна начинаться заранее, за указанное время до запланированного времени начала работы барабана. Таким образом, буфер должен страховать барабан от простоев.
- Принцип запуска материалов в производство до выхода изделий на барабан — это «веревка». Веревка «дергает» материалы со склада в соответствии с тактом барабана, причем только в том количестве, которое нужно для барабана. Ни в коем случае нельзя выдавать материалов больше, чем требуется барабану — в противном случае РЦ до барабана могут испытывать сложности и их пропускная способность может стать меньше, чем у барабана.
В данной статье мы не будет детально описывать плюсы и минусы данной методики, а также нюансы APS в рамках 1С:ERP. Однако некоторые особенности, мы отметим:
- Cоздается первое допустимое расписание.
- Это расписание является «Сильно приближенным». Расчет по ВРЦ не позволяет уплотнить загрузку ВРЦ настолько, насколько это позволяет полноценные APS, т. е. для нормальной работы требуется буферизация, искусственное занижение доступного фонда работы и не 100% загрузка оборудования в графике.
- До версии 2.5.6 1С:ERP учитывал только НЗП в наличии, т. е. «будущие» НЗП никак не учитывались. После 2.5.6. это ограничение снялось, но только в случае использования спецификаций в режиме «ПФ создается в процессе производства».
- Переналадки Барабана 1С:ERP не планирует.
- Буферы перед узкими РЦ задаются вручную и складываются в случае наличия нескольких узких РЦ, что делает допустимое расписание совсем уж не оптимальным.
Если суммировать все вышесказанное, то 1С:ERP строит приблизительный график совокупной загрузки мощностей, отдавая все полномочия по его исполнению и планированию операций локальному диспетчеру цеха, что для сложных производств приводит к насущной необходимости использования функционала «Оперативного планирования» 1С:ERP. Какие же особенности следует учитывать в этом случае?
Если говорить коротко, то к сожалению никакой методики для оптимизации составления производственного расписания на момент написания статьи (версия 2.5.7) нет. Текущий алгоритм использует переборный вариант оптимизации, что естественно приводит к факториальному росту сложности и является нерешаемой задачей даже для простейших случаев. Поэтому на выходе алгоритма «Оперативного планирования» 1С:ERP планировщик получает Допустимое расписание, но при этом:
- операции уже распределяются по РЦ, а не по ВРЦ;
- учитываются переналадки;
- перестают учитываться потребности в материалах.
Подбираем альтернативные пути решения задач Теории расписаний
Чтобы рассмотреть подробнее современные методы решения задачи ТР давайте еще раз обратимся к теории. Методы решения задач комбинаторной оптимизации разделяют на:
- Эвристические алгоритмы, в том числе вероятностные и локальный поиск. Класс алгоритмов, правильность которых для всех возможных случаев не доказана, но про которые известно, что они дают достаточно хорошее решение в большинстве случаев.
- Точные методы
- Метод динамического программирования (в том числе линейное или квадратичное программирование). Класс алгоритмов, которые решают сложные задачи путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой, выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной.
- Метод ветвей и границ. Класс алгоритмов, которые решают задачу путем последовательного разбиения множества допустимых решений. На каждом шаге метода элементы разбиения (подмножества) подвергаются анализу – содержит ли данное подмножество оптимальное решение или нет.
Оба алгоритма в общем случае не позволяют решать задачу ТР за полиномиальное время и характеризуются «проклятием размерности» — сложность их катастрофически возрастает с увеличением размерности задачи.
Эвристические алгоритмы относят к приближенным алгоритмам. Обычно это быстрые полиномиальные алгоритмы, основанные на какой либо догадке о свойствах оптимальных решений. Среди них выделяют алгоритмы с:
- гарантированными оценками качества,
- регулируемой точностью.
Отметим что из-за своей общности эвристические алгоритмы «в базе» не обладают ни гарантированными оценками качества, ни регулируемой точностью при решении задач ТР.
В качестве платформы для решения задачи составления внутрицехового планирования был выбран MatLab. У него довольно простой язык, весьма похожий по своей нотации на Python и есть возможность параллельных вычислений. В нашей библиотеке на MatLab было реализовано довольно большое число различных алгоритмов для составления расписания и мы продолжим говорить о них в следующих публикациях подробно. В этой статье начнем с рассмотрения Метода ветвей и границ (далее B&B, branches and bounds), который является точным методом и генетического алгоритма, а также их композиции.
Метод B&B
Три основных элемента этапа B&B:
- Ветвление
Исходная задача разбивается на подзадачи, определенные подмножествами допустимых решений. Ветвление — это рекурсивный процесс, т. е. каждая подзадача в свою очередь является базисом для другого ветвления. В процессе ветвления образуется дерево поиска оптимального решения. При этом исходная задача называется корнем, а подзадачи — ветками или потомками. - Верхняя оценка (граница)
Используется в алгоритме, чтобы предварительно принять решение о перспективности той или иной подзадачи, т. е. оценить возможность того, что подзадача содержит оптимальное решение исходной задачи. Например, верхними оценками могут выступать жесткие даты необходимой отгрузки. Т.е. если в нашем примере у Задания 1 необходимая дата отгрузки 700, то любое расписание, у которого конечное время исполнения Задания 1 больше 700 может быть отброшено. - Нижняя оценка (граница)
Используется в алгоритме, для отсечения ветвей, которые не имеет смысла рассматривать.
Чтобы построить алгоритм, основанный на методе B&B, необходимо определить способ ветвления и способы вычисления нижних и верхних оценок.
В качестве примера рассмотрим как этот алгоритм работает для нашей исходной задачи. Дерево решения задачи приведено на рисунке 17.
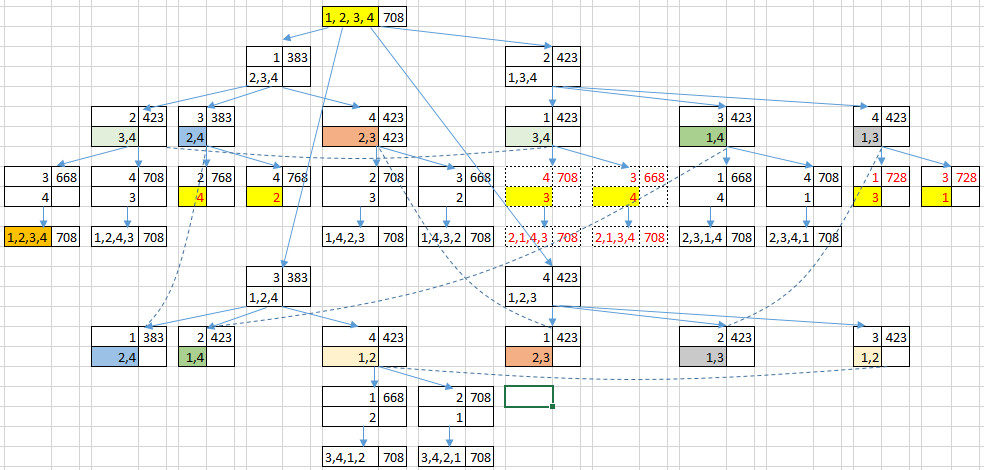
Рисунок 17. Решение тестовой задачи алгоритмом B&B
Напомним, что мы должны получить расписание вида S={1, 2, 3, 4}. Пусть это и будет наше первое допустимое расписание. Для упрощения задачи будем считать целевую функцию Cmax. Из таблицы 3 мы знаем, что для этого расписания Cmax = 708. Считаем, что это лучшее значение 708.
Далее мы выбираем точку разбиения первого уровня, это может быть любое Задание, тогда подзадачи первого уровня {1–2, 3, 4},{2–1, 3, 4},{3–1, 2, 4},{4–1, 2, 3}. Первоначальная нижняя граница для нашей задачи будет равна {383, 423, 383, 423} для каждой из ветвей.
Вызываем рекурсию и теперь разбиения второго уровня для первой ветки выглядят так {1, 2–3, 4},{1, 3–2, 4},{1, 4–2, 4}. Нижние границы {423, 383, 423}.
Вызываем рекурсию и тогда разбиения третьего уровня для первой ветки второго уровня выглядят так {1, 2, 3–4},{1, 2, 4–3}. Нижние границы {668, 708}.
Мы видим, что для второй ветки разбиения третьего уровня мы уперлись в границу 708 и если бы была возможность опуститься еще на один уровень, то рассматривать эту подзадачу было бы бессмысленно. Упираясь в четвертый уровень {1,2,3,4}, мы обновляем рекорд.
Для того, чтобы сократить перебор вариантов для нашей задачи можно воспользоваться свойством парности РЦ, в этом случае все четные парные перестановки работ эквиваленты. Такие свойства задачи относят к отношениям доминирования.
Пройдя по всем веткам дерева мы получим список оптимальных расписаний с одинаковым значением Cmax=708, это {1, 2, 3, 4}, {1, 4, 2, 3}, {1, 4, 3, 2}, {2, 3, 1, 4}, {2, 3, 4, 1}, {2, 3, 1, 4}, {3, 4, 1, 2}, , {3, 4, 2, 1}. Далее можно выбрать решение случайно из них, либо добавить дополнительную функцию минимизации, например минимизация суммарного времени запаздывания и выбрать лучшее расписание по этому критерию.
Отметим, что в этом примере мы не использовали никаких Верхних оценок, вследствие того, нахождение их в общем случае непростая задача, так как это обычно аналитическая оценка и удается ее получить только для специальных задач ТР.
Как правило, трудоемкость алгоритма B&B растет экспоненциально с ростом размерности задачи, однако здесь очень большое значение имеет выбор верхних и нижних границ. Сложность состоит в том, что для задач ТР не существует заранее предопределенной формулы нахождения верхних и нижних границ и зачастую они подбираются под конкретную задачу. Более того, в большинстве реальных задач для них используются Эвристики, в связи с чем у вроде бы точного метода B&B возникают Гарантированные оценки качества и скорости.
Генетический алгоритм
Далее рассмотрим пример использования эвристического подхода решения задачи ТР используя для ознакомления метод Генетической эволюции (ГА, генетический алгоритм).
Общая схема работы ГА применительно к задачам ТР следующая:
- Формируется начальная популяция, состоящая из некоего числа N допустимых согласно условий предшествования расписаний, представленных в виде списков работ в порядке их предпочтения.
- Из популяции выбираются пары решений, и над ними выполняется операция скрещивания. В большинстве методов от пары решений получается пара новых решений, которая образует новое поколение, состоящее из N решений.
- Для нового поколения решений применяется оператор мутации. Суть данного шага заключается в искусственном изменении порядка следования операций в списке. Для каждого решения I в списке работ LI для позиций i = 1, …, J–1, операции iIj и iIj + 1 c вероятностью pmut меняются местами, но только в том случае, если это не приводит к нарушению условий предшествования. Таким образом, получается новая популяция, состоящая из N особей прошлого поколения и N особей нового. Итого на данном шаге имеем популяцию, состоящую из 2N особей.
- К особям популяции применяется оператор отбора. Для этого по каждому списку работ, входящему в состав популяции, строится расписание, по которому вычисляется качественный критерий полученного расписания, например, время завершения Сmax. Список, состоящий из особей популяции, сортируется по убыванию критерия качества и удаляется N особей из хвоста этого списка. Таким образом, размер популяции приводится к исходному, состоящему из N лучших из 2N полученных на шаге 3 особей. Также рекомендуется предварительно очистить популяцию от клонов, то есть одинаковых особей.
- Шаги 2–4 повторяются до тех пор, пока не выполнится критерий остановки работы алгоритма. Это может быть как достижение заданного количества поколений (повторов выполнения шагов 2–4), так и достижение процессорного времени, отведенного на решение задачи, или другие критерии.
В качестве примера рассмотрим как этот алгоритм работает для нашей исходной задачи. Алгоритм решения задачи для первой эпохи приведен на рисунке 18.

Рисунок 18. Пример ГА для первой эпохи
Генетический алгоритм начинается с выбора какой-либо, чаще всего полученной эвристическим алгоритмом, популяции. Пусть это будет 4 допустимых решения (особи): {1, 2, 3, 4}, {2, 1, 3, 4}, {3, 1, 2, 4}, {4, 1, 2, 3}. Скрестим эти особи попарно, при этом для точка кроссовера случайно выбирается для 1-й пары как 2, для 2-й как 3. Получим для 1-й пары: {1, 2, 4, 3}, {2, 1, 3, 4}. Для 2-й пары: {4, 1, 2, 3}, {3, 1, 2, 4}, мы получили исходные значения поэтому дальнейшую мутацию мы сделаем с вероятностью 100%.
Для 1-й пары пусть также выпала мутация. Для мутации нам необходимо опять же случайно выбрать пару Заданий для перестановки. Зная свойство «четные парные перестановки работ эквиваленты» пары будем выбирать обязательно из разных четных групп. В итоге мы получим набор из 4-х хромосом: {1, 3, 4, 2}, {4, 1, 3, 2}, {4, 2, 1, 3}, {2, 1, 3, 4}.
Рассчитав для каждой из них Cmax, включив в исходную таблицу и отсортировав по Cmax мы получим Таблицу 5.
Далее шаги алгоритма 2-4 повторяются для 4-х верхних строк. Строки с 5-й по 8-ю запоминаются как не прошедшие отбор, и если после кроссовера и мутации мы получим особь, входящую в этот список, то она автоматически отбрасывается и мутация проводится еще раз.
Таблица 5. Набор особей после первой эпохи
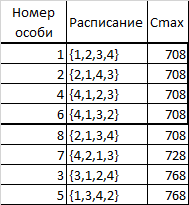
После 2-й эпохи мы можем получить такой список:
Таблица 6. Набор особей после второй эпохи
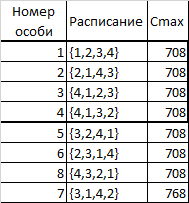
Напомним, что общего правила останова для алгоритма ГА не существует и обычно алгоритм останавливается после достижения какого-либо ограниченного количества эпох либо если состав лучших хромосом после эпохи несколько раз не улучшается.
В нашем примере, мы остановимся после 2-х эпох и лучшее расписание {1, 2, 3, 4}.
К основным преимуществам ГА относится:
- концептуальная простота;
- гарантированный порог остановки (количество эпох);
- параллелизм.
К основным недостатком ГА относится:
- отсутствие гарантированных оценок качества;
- крайняя зависимость от выбора начальной популяции;
- отсутствие эффективных критериев окончания работы (количество эпох);
- сходимость к локальным экстремумам в общем случае не гарантируют нахождение глобального экстремума.
Гибридный поиск оптимального расписания
Также отметим наличие возможности использовать в рамках ГА гибридного поиска. Например, используя на отдельных этапах отношения доминирования, эвристики, верхние и нижние границы полученные, с помощью B&B. В нашей библиотеке в частности используются проверки отношении доминирования, верхние границы на основе алгоритма Джонсона и локальный поиск.
Как это работает вновь рассмотрим на нашем примере. Теперь между шагом 3 и 4 основного алгоритма вставим локальный поиск с помощью B&B с уровня, когда оптимизируются 3 задания. Алгоритм решения задачи для первой эпохи приведен на рисунке 19.
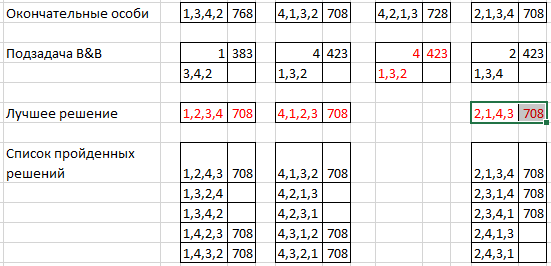
Рисунок 19. Пример B&B для первой эпохи ГА
Примечание: Третья особь на рисунке эквивалентна 2-й, поэтому эта особь далее не используется.
После первой эпохи алгоритма с использованием B&B состав особей не изменился (новых не появилось) поэтому алгоритм можно завершить.
Отметим, что в нашей разработке запрограммированы и другие эвристические подходы, такие как Метод муравьиных колоний (SACO) и Табу-поиск (Tabu-search). Подробно рассказать про эти методы мы предполагаем в следующей статье из этого цикла.
Теперь, когда мы разобрали математическую часть постановки задачи построения оптимальных расписаний и методы ее решения мы кратко расскажем об архитектурной части нашего решения.
Архитектура нашего решения оптимизации внутрицехового расписания для 1С:ERP
Как мы и писали ранее платформа 1С лишь с малой вероятностью станет бороться на поле математических расчетов и решения задач оптимизации, поэтому в качестве движка нашей разработки выбран один из лидеров этой отрасли — программный комплекс Matlab компании Mathwork.
Интеграция между 1С:ERP и Matlab была выполнена на уровне базы данных — выгрузка и загрузка данных в 1С:ERP происходит путем вызова процедур чтения и записи в таблицы SQL из Matlab. Безусловно, возможно множество альтернативных подходов реализации этой интеграции.
В качестве источников данных для расчетов используются:
- Документ.ЭтапПроизводства2_2,
- РегистрСведений.Длительность
Переналадки, - РегистрСведений.Очередь
ПроизводственныхОпераций, - РегистрСведений.График
ЭтаповПроизводства2_2, - РегистрСведений.Пооперационное
Расписание2_2, - РегистрСведений.Доступность
РабочихЦентров.
Здесь следует отметить очень важный момент. Для расчетов мы используем уже готовое допустимое расписание, сформированное 1С:ERP в процессе обработки «Пооперационное планирование», при этом мы отключили «оптимизатор» (двойной цикл по переналадкам). В этом случае должен быть заполнен регистр сведений ПооперационноеРасписание2_2 как на рисунке 20.
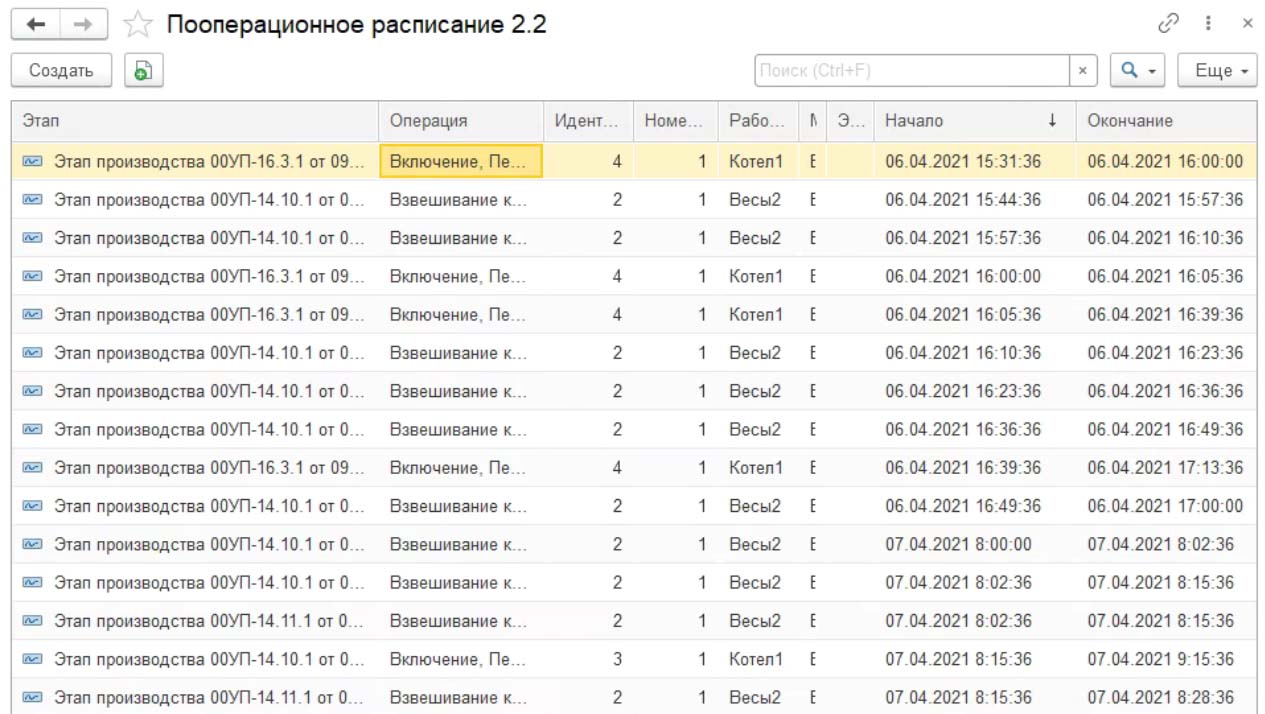
Рисунок 20. Вид регистра сведений ПооперационноеРасписание2_2
Концептуальная схема расчетов состоит из следующих этапов:
- Получаем данные из 1С:ERP.
- Преобразуем данные из таблиц в матрицы.
- Снижаем размерность задачи.
- Ищем оптимальное расписание.
- Составляем полное расписание.
- Записываем данные в 1С:ERP.
Кратко прокомментируем особенности каждого из этапов.
На этапе получения данных из 1С:ERP используется стандартный драйвер ODBC, пример вызова из Matlab можно увидеть на рисунке 21.
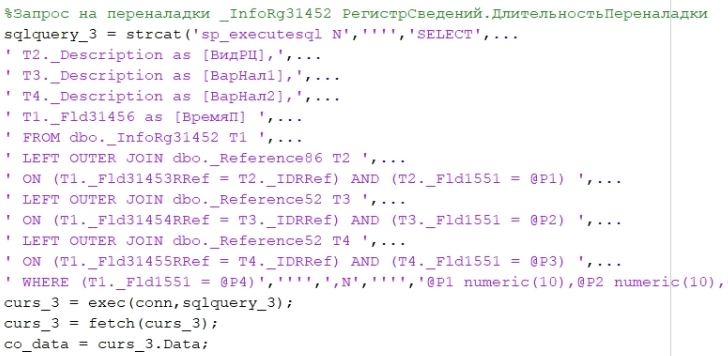
Рисунок 21. Пример выполнения запроса из Matlab
Этап преобразования данных необходим для преобразования двумерных таблиц в матрицы. Например, для кода, указанного на рисунке 21 мы получим данные в виде таблицы на рисунке 22.
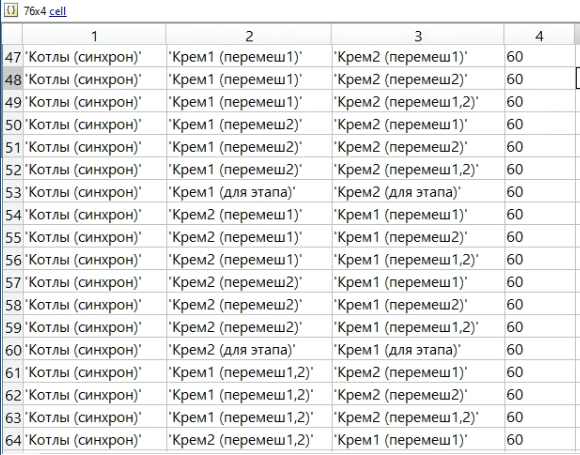
Рисунок 22. Таблица переналадки после выгрузки из 1С:ERP
Далее необходимо таблицу переналадки связать с Заданиями для чего необходимо выполнить алгоритм:
1. Цикл по Заказам
a. Ищем операции с РЦ “Котлы (синхрон)”
b. Цикл по всем строкам из a.
i. Цикл по оставшимся Заказам
1. Ищем операции с РЦ “Котлы (синхрон)”
2. Цикл по всем строкам из i.1.
a. Если варианты наладки различные, то переналадка
есть, иначе переналадки нетПосле преобразования мы получим матрицу переналадки на РЦ «Котлы (синхрон)» на рисунке 23. По столбцам и строкам идут номера заданий из нашего примера, что соответствует таблице 2.
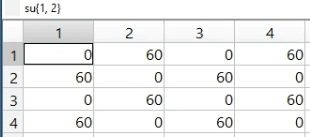
Рисунок 23. Матрица переналадки в Matlab
Этап снижения размерности необходим для того, чтобы снизить размер входных матриц, а следовательно и трудоемкость расчетов. Этот этап может сильно зависеть от исходной постановки задачи, т. е. от типа производства, взаимоотношений с клиентами и т. п.
Так, если в нашем примере дата необходимой отгрузки для Крема 1 для Задания 1 и Задания 3 совпадали бы или отличались менее чем на 2% от суммарной длительности работ, то оба Задания бы схлопнулись в одно. Важно, что Задания при этом непременно должны находиться на одинаковых этапах обработки.
Также во многих случаях можно и нужно снижать размерность последовательности операций на РЦ, объединяя их по принадлежности к одному РЦ и убирая часть ненужных для расчета операций, например складирование, остывание, высыхание, иногда и контрольные операции.
Вновь возвращаясь к нашему примеру, если посмотреть исходную технологическую карту, то после операции «Перемешивание» должна планироваться операция «Уборка». Однако, вследствие того, что ограничений по этой операции нет, и практически всегда найдется сотрудник, который выполнит эту операцию, то влияния на оптимизацию расписания эта операция не имеет и следовательно, для нашей задачи эту операцию можно и нужно опустить.
Этап поиска оптимального расписания содержит в себе целый ряд алгоритмов описание которых было выше в статье. Естественно, что использование всех алгоритмов в промышленном режиме не является целесообразным, поэтому каждый из алгоритмов является отключаемым в настройках модуля.
Однако на этапе исследования мы рекомендовали бы тестировать все возможные алгоритмы, т. к. согласно теореме «Бесплатного сыра не бывает» универсального алгоритма работающего одинаково хорошо во всех случаях не существует. Следовательно, каждый из алгоритмов вполне может «выстрелить» в зависимости от постановки и исходных данных. Также отметим, что на выбор «оптимального» алгоритма совместно влияют:
- качество оптимизации,
- ограничение на время расчета.
Для оценки качества оптимизации применяется алгоритм B&B на небольшом размере исходных данных, который, напомним, всегда выдает оптимальное решение.
Следует отметить, что именно на этапе поиска расписания полноценно используются преимущества возможностей Matlab такие как:
- Параллельные вычисления (parfor, createJob, createTask).
- Расчет In-memory.
- Быстрые операции над матрицами, включая автоматическую оптимизацию памяти при работе с разряженными матрицами, быстрые расчеты обратных матриц и операции с матрицами на GPU.
- Наличие встроенных функций оптимизации, включая эвристические алгоритмы.
Этап составления полного расписания содержит в себе функции обратные этапу снижения размерности. Т.е. мы:
- восстанавливаем все «схлопнутые» Задания как отдельные сущности;
- восстанавливаем все пропущенные операции из маршрутной карты.
Этап записи ограничивается в настоящий момент коррекцией регистра сведений Пооперационное
Расписание2_2, что необходимо для визуализации полученного расписания, но недостаточно для полноценной работы, т. к. естественно требуется внести изменения во все остальные связанные регистры.
Для того чтобы завершить наш контрольный пример с выпуском крема, увеличим число Заданий до 24 (4 Заказа, по два на каждый Крем, количество в заказах подобрано так, чтобы он делился на 6 партий пропорционально максимальной загрузке на Котел) и посмотрим как справится стандартный алгоритм 1С:ERP и наша библиотека на базе Matlab.
На рисунке 24 мы видим расписание, которое построил нам встроенный алгоритмом планирования Пооперационного планирования. Как видим дата последней операции 14 апреля.
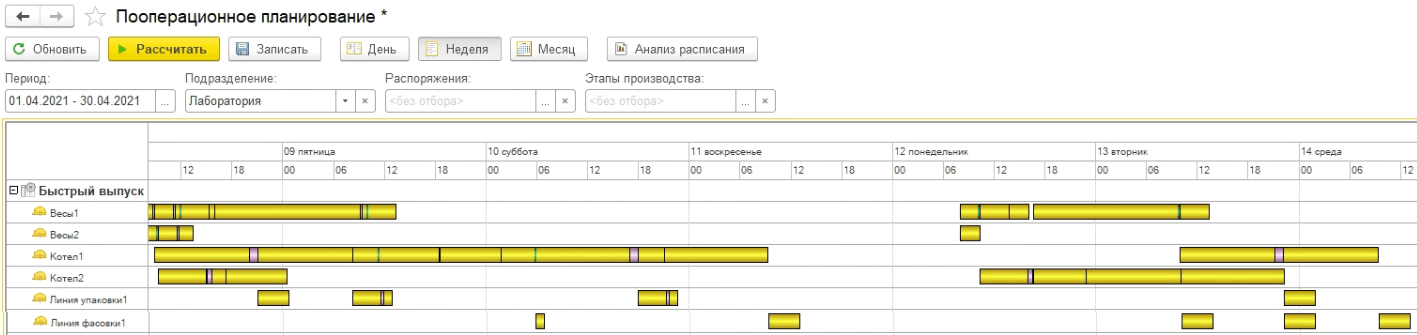
Рисунок 24. Расписание, составленное встроенным алгоритмом 1С:ERP
На рисунке 25 мы видим расписание, которое построила наша программа на базе Matlab. Дата последней операции 12 апреля.
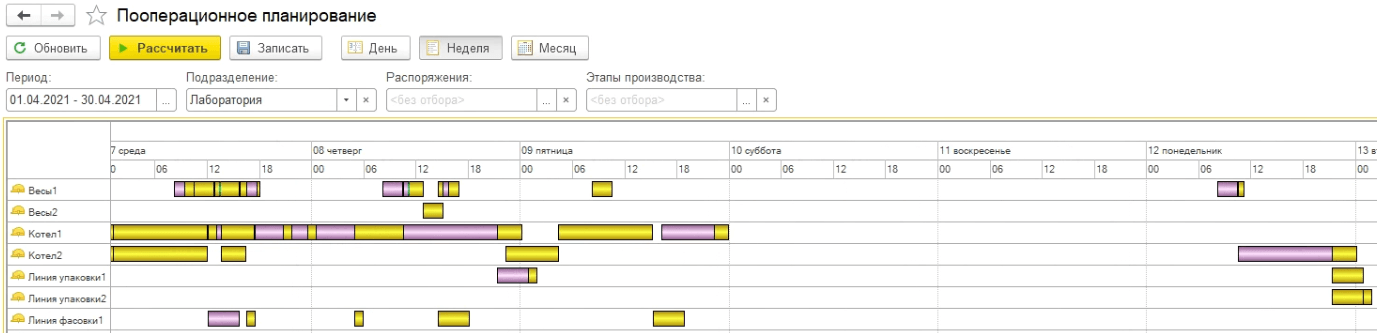
Рисунок 25. Расписание, составленное с помощью Matlab
Когда переход с допустимого на оптимальное расписание производства оправдан?
В заключении хотелось бы поднять еще один немаловажный аспект рассмотренной задачи. Ответим на вопрос: по каким критериям стоит судить, пора ли задуматься о переводе производства с допустимого на оптимальное расписание?
Ответ складывается из следующих составляющих:
- Загруженность производства
В теории ограничений и Kaizen одним из основных признаков некачественного производственного планирования являются очереди перед узким местом. Поэтому если вы видите гору заготовок перед каким-то РЦ — это один из признаков того, что нужно заниматься оптимизацией планирования. По опыту такая ситуация возникает при загрузке производства уже на уровне 70–80%. Особенно эта задача важна для производств, у которых узкие места «плавающие» и зависят от структуры портфеля заказов. - Качество спецификаций
Золотое правило «garbage in — garbage out» применимо для этой задачи на все 100%. Даже отклонение в оценке работ в 10% на одном РЦ в последовательности из 10 РЦ может дать отклонение в 100% во всей цепочке. Поэтому, чем выше для компании уровень требований поставки «точно в срок», тем жестче становятся требования к качеству исходной производственной документации. К примеру, если нужно добиться отклонения в один день, то суммарное отклонение длительности работ по технологическому маршруту не должно превышать нескольких часов. - Качество прослеживаемости изделий
Необходимо понимать, что качественное внутрицеховое планирование возможно только в условиях внедренного MES. Ведь если перепланировать необходимо каждую смену (топовые мировые компании перепланируют каждые 2–3 часа), то на момент планирования всегда нужна полная информация о всех составляющих всех запущенных изделий, состояния складов, информации о качестве материалов и ПФ, информации о состоянии оборудования и т.д. - Уровень конкуренции и уровень штрафов за недопоставку
Задача оптимизации возникает естественным образом для компаний, которые находятся в высококонкурентном сегменте бизнеса. В условиях, когда каждый клиент является важным и удержание клиентов — приоритетная задача. В этих условиях отгрузка «точно в срок» является очень важным преимуществом. При этом штрафы за недопоставку складываются не только и не столько из условий договоров, сколько из поддержания имиджа компании. - Экономия
Посчитать выгоду от оптимизации расписания довольно просто. К примеру, компания выпускает продукцию на 100 млн руб. в месяц и загрузка производства близка к 100%. Уплотнение графика производства даже на 10% поможет компании дополнительно выпускать продукцию на 10 млн руб. не говоря о выгодах от снижения запасов, уменьшения штрафов за недопоставку и пр. Безусловно, степень уплотнения графика зависит от самого производства и портфеля заказов, но по опыту можно добиться 20 и даже 30% уплотнения.
Суммируя вышесказанное — задачу оптимизации производственного расписания невозможно решить саму по себе, т. к. она лишь часть бизнес-процесса планирования, но она задает достаточно жесткие ограничения к этому процессу. Однако и эффект от ее решения обычно превосходит многие другие способы оптимизации бизнес-процессов, поэтому для компаний, которые сделали первичную оптимизацию и стоят перед выбором, что же делать дальше — это очень хороший способ сделать прорыв.
Основная же проблема кроется в теореме «об отсутствии бесплатных завтраков» (no free lunch theorem). Она говорит, что нет универсального метода решения сложных задач и оптимальный метод сильно зависит от самой постановки задачи. Поэтому один или два алгоритма, реализованные в современных пакетах оптимизации производственного расписания (сейчас это обычно Эвристика или ГА) дают хорошую оптимизацию в строго ограниченном количестве случае, для узкого круга задач. «Заточенный» под конкретное производство алгоритм даст гораздо лучшее решение, но требует наличия в команде проекта хорошего специалиста по оптимизации или наличия хорошего бизнес-партнера, который такие задачи уже решал.
Большое количество интересных технических докладов мы презентовали в 2020 году на 1C-RarusTechDay. Посмотреть их можно здесь.
В 2021 году 1C-RarusTechDay вновь пройдёт в онлай-формате и будет доступен для всех желающих. Чтобы не пропустить анонс конференции и получить ссылку на трансляцию — подписывайтесь на наш канал в Telegram или почтовую рассылку.
От экспертов «1С-Рарус»

























