Нужно больше графов в 1С

Эта вторая статья цикла, посвященного работе с графовыми структурами. Сегодня мы поговорим о практической задаче визуализации сетевого маршрута, построении матрицы смежности, поиске циклов в графе и связанными с ними сложностями.
Познакомиться с первой статьёй — «От экспертов „1С‑Рарус“: Построение и визуализация древовидных структур в 1С» — можно здесь.

Обратная маршрутизация затрат — от отчётов по финансовому результату к исходным документам управленческого учёта

В организации используется отдельная конфигурация для финансового учета. На ней лежат функции расчета финансового результата, учета бюджета, быстрого выполнения структурированных отчетов для руководства. В конфигурации есть и другие возможности для эффективного ведения финансового менеджмента.

Один из процессов — «Расчет финансового результата» — устроен по схеме поэтапного выполнения шагов по движению сумм в регистре с одних аналитик на другие согласно сценарию. Алгоритм шагов настраивается согласно регламенту и, как правило, сценарий включает в себя ряд агрегаций на общие статьи затрат и распределение между прибылеобразующими подразделениями.

Самый сложный сценарий организации насчитывает более 600 шагов. Также могут присутствовать операции взаимного оказания услуг, для этого в сценариях предусмотрен блок итерации, в котором некий список шагов выполняется циклически несколько раз, с постепенно уменьшающимися суммами согласно долям.

Ввиду масштабности и сложности устройства процесса — часто бывает проблематично четко ответить на вопрос откуда пришли затраты на конкретное подразделение. Отсюда возникла задача по созданию отчета, который в явном виде показывал бы обратную маршрутизацию затрат, до начальной точки в виде документов, отражающих управленческие операции.

• Целевая функция задачи.
  • Ответить на вопрос в общем виде о том, как сложилась сумма на определенной аналитике учета.
• Сложность задачи.
  • Огромное количество движений. Миллионы и десятки миллионов.
  • Наличие циклов — самые простые это взаимонаправленные движения, также часть связана с наличием блока итерации.

Постановка задачи носит универсальный характер, т. е. необходимо подвести под решение математический аппарат, не завязываясь на прикладные сущности. А значит нужно привести исходные данные к математической абстракции. Рассмотрим варианты архитектурной организации учета.

Варианты архитектурной организации учета в разных системах

«Классический» вариант

Когда измерения представлены в регистре в явном виде (организация, номенклатура, партия и т. д.).Например, конфигурация 1С:УНФ, регистр накопления «Запасы и затраты»:

С использованием ключей аналитик

В этом случае измерение представляет собой объединение многих аналитик. Такой сборной аналитикой проще манипулировать на уровне запросов.

Например, конфигурация 1С:ERP, в регистре накопления «СебестоимостьТоваров» используются измерения «АналитикаУчетаНоменклатуры» и «АналитикаУчетаПартий», которые включает в себя множество детальных аналитик — номенклатура, серия, контрагент, договор и др.

Давайте разберемся, как использовать эти структуры для математических абстракций.

Математическая основа преобразования архитектурной иерархии регистров и аналитик 1С в абстракции

В базе, о которой мы говорим, учет устроен по классическому принципу. Входными данными для задачи являются движения оборотного регистра накопления «Расходы затраты», который содержит следующие поля:

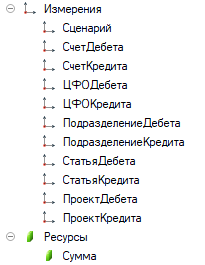
Для простоты опустим некоторые измерения и представим движения такой схемой:

Счет1 + Подразделение1 + Статья1 → Счет2 + Подразделение2 + Статья2 — Сумма

Примечание: здесь и далее для простоты примем одно допущение — направлением движения затраты всегда считаем от узла Кт к узлу Дт, таким образом все ребра для нас имеют одно направление. Условно назовем узел кредита как исходящий, а узел дебета как входящий.

Путь движения затрат по своей сути является сетевым маршрутом, который можно представить в виде ориентированного связного графа, в котором конечной точкой условно можно назвать узел со счетом финреза.

Движения регистра — в матрицу смежности

Для решения задачи в математическом ключе необходимо преобразовать движения регистра в матрицу смежности.

Первое с чего нужно начать — это идентификация узлов. Наш регистр устроен по «классической» схеме (см. выше), то есть в движении присутствуют все детализированные измерения, с этим достаточно неудобно работать. В рамках задачи мы можем идентифицировать список аналитик исходящих и входящих узлов в виде одной аналитики — уникального номера. Для этого возьмем список движений, сгруппируем все возможные аналитики и проставим каждому набору свой номер с помощью встроенной функции в запросе АВТОНОМЕРЗАПИСИ():

Далее соединив таблицу идентификаторов с таблицей движений получим таблицу матрицы смежности вида:

• идентификаторУзлаДт,
• идентификаторУзлаК,
• сумма.

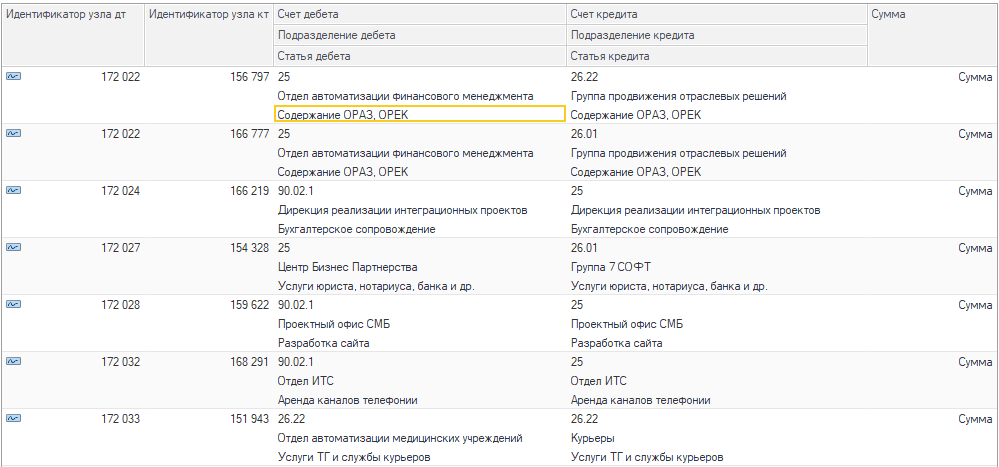
Ещё одна подзадача — учесть взаимное распределение.

Например, бухгалтерия оказывает услугу юр. отделу, юр. отдел оказывает услугу бухгалтерии. В регистре это выглядит как разнонаправленные движения.

Такой пример является петлей и желательно от неё избавиться на этапе подготовки матрицы. Ниже представлен вариант, как это можно сделать в запросе. Условно разделим выборку на три подпакета:

1. Ребра «прямого» направления, для которых есть пара с обратным движением.
2. Ребра обратного движения для п. 1.
3. Остальные ребра, для которых пары нет.

В текущем примере «прямое» направление выбрано условно случайно по величине номера узла, т. к. для текущей задачи это не критично.

ВЫБРАТЬ

  "Взаимонаправленная сторона входящих узлов" КАК ВидПакета,

  ДанныеДт.СчетДебета КАК СчетДебета,

  ДанныеДт.ПодразделениеДебета КАК ПодразделениеДебета,

  ДанныеДт.СтатьяДебета КАК СтатьяДебета,

  ДанныеДт.СчетКредита КАК СчетКредита,

  ДанныеДт.ПодразделениеКредита КАК ПодразделениеКредита,

  ДанныеДт.СтатьяКредита КАК СтатьяКредита,

  ДанныеДт.Сумма КАК Сумма,

  ДанныеДт.ИдентификаторУзлаДт КАК ИдентификаторУзлаДт,

  ДанныеДт.ИдентификаторУзлаКт КАК ИдентификаторУзлаКт

  ИЗ

  ДанныеСИдентификаторами КАК ДанныеДт

  ВНУТРЕННЕЕ СОЕДИНЕНИЕ ДанныеСИдентификаторами КАК ДанныеКт

  ПО (ДанныеДт.ИдентификаторУзлаДт = ДанныеКт.ИдентификаторУзлаКт)

  И (ДанныеДт.ИдентификаторУзлаКт = ДанныеКт.ИдентификаторУзлаДт)

  И (ДанныеДт.ИдентификаторУзлаДт < ДанныеДт.ИдентификаторУзлаКт)
СГРУППИРОВАТЬ ПО

  ДанныеДт.СчетДебета,

  ДанныеДт.СтатьяДебета,

  ДанныеДт.СчетКредита,

  ДанныеДт.ПодразделениеДебета,

  ДанныеДт.ПодразделениеКредита,

  ДанныеДт.СтатьяКредита,

  ДанныеДт.Сумма,

  ДанныеДт.ИдентификаторУзлаДт,

  ДанныеДт.ИдентификаторУзлаКт
ОБЪЕДИНИТЬ ВСЕ
ВЫБРАТЬ

  "Взаимонаправленная  сторона исходящих узлов",

  ДанныеКт.СчетКредита,

  ДанныеКт.ПодразделениеКредита,

  ДанныеКт.СтатьяКредита,

  ДанныеКт.СчетДебета,

  ДанныеКт.ПодразделениеДебета,

  ДанныеКт.СтатьяДебета,

  -ДанныеКт.Сумма,

  ДанныеКт.ИдентификаторУзлаКт,

  ДанныеКт.ИдентификаторУзлаДт

  ИЗ

  ДанныеСИдентификаторами КАК ДанныеДт

  ВНУТРЕННЕЕ СОЕДИНЕНИЕ ДанныеСИдентификаторами КАК ДанныеКт

  ПО ДанныеДт.ИдентификаторУзлаДт = ДанныеКт.ИдентификаторУзлаКт

  И ДанныеДт.ИдентификаторУзлаКт = ДанныеКт.ИдентификаторУзлаДт

  И (ДанныеДт.ИдентификаторУзлаДт < ДанныеДт.ИдентификаторУзлаКт)
СГРУППИРОВАТЬ ПО

  ДанныеКт.СтатьяДебета,

  ДанныеКт.СчетКредита,

  ДанныеКт.ПодразделениеКредита,

  ДанныеКт.СтатьяКредита,

  ДанныеКт.СчетДебета,

  ДанныеКт.ПодразделениеДебета,

  ДанныеКт.Сумма,

  ДанныеКт.ИдентификаторУзлаКт,

  ДанныеКт.ИдентификаторУзлаДт
ОБЪЕДИНИТЬ ВСЕ
ВЫБРАТЬ

  "Остальные  ребра",

  ДанныеДт.СчетДебета,

  ДанныеДт.ПодразделениеДебета,

  ДанныеДт.СтатьяДебета,

  ДанныеДт.СчетКредита,

  ДанныеДт.ПодразделениеКредита,

  ДанныеДт.СтатьяКредита,

  ДанныеДт.Сумма,

  ДанныеДт.ИдентификаторУзлаДт,

  ДанныеДт.ИдентификаторУзлаКт

  ИЗ

  ДанныеСИдентификаторами КАК ДанныеДт

  ЛЕВОЕ СОЕДИНЕНИЕ ДанныеСИдентификаторами КАК ДанныеКт

  ПО (ДанныеДт.ИдентификаторУзлаДт = ДанныеКт.ИдентификаторУзлаКт)

  И (ДанныеДт.ИдентификаторУзлаКт = ДанныеКт.ИдентификаторУзлаДт)

  ГДЕ

  ДанныеКт.СчетДебета  ЕСТЬ NULL 

Переход от сетевого маршрута к дереву

В первичной постановке было принято решение о визуализации маршрута в виде дерева, полученного с помощью механизма построения иерархии СКД путем соединения матрицы смежности с самой собой. При этом крайне важно до передачи данных в СКД избавиться от циклов в графе.

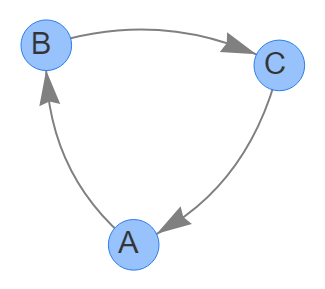
Пример простого цикла:

Для наглядности приводим пример тройного цикла обнаруженный в реальных данных:

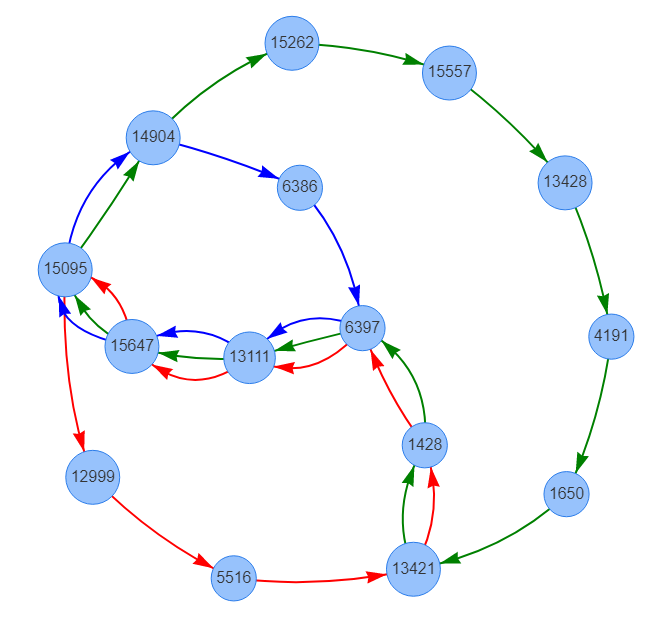
Попытка решить проблему «в лоб», используя алгоритм поиска в глубину на 1С не дала результата в обозримое время и это ожидаемо, т. к. число ребер достаточно велико. Поэтому мы начали искать пути ограничения области поиска, один из них — вычисление компонент сильной связности.

Вычисление компонент сильной связности (КСС)

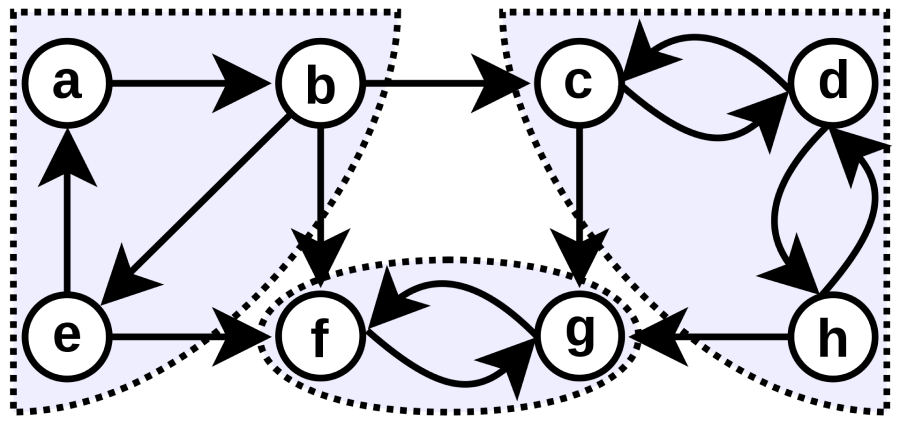
Ориентированный граф с показанными компонентами сильной связности (Источник: wikipedia.org)

Для поиска КСС мы ознакомились с двумя механизмами

1. Методы решения систем линейных алгебраических уравнений 1С.
2. Библиотека Python NetworkX.

Методы решения систем линейных алгебраических уравнений (СЛАУ) 1С для поиска компонент сильной связности

Как следует из названия, данный механизм позволяет решать системы линейных алгебраических уравнений. Например, подобные задачи возникают при расчете себестоимости. Помимо этого, механизм СЛАУ 1С позволяет получать компоненты слабой и сильной связности графа, используя метод ПолучитьКомпонентыСвязности объекта РасчетСистемЛинейныхУравнений.

Подробнее про данный механизм можно почитать на ИТС в руководстве разработчика в разделе «Прочие механизмы» (its.1c.ru/db/v8320doc#bookmark:dev:TI000002183).

Мы тестировали механизм на разных наборах. На небольших примерах всё отрабатывало корректно, как указано в руководстве ИТС.

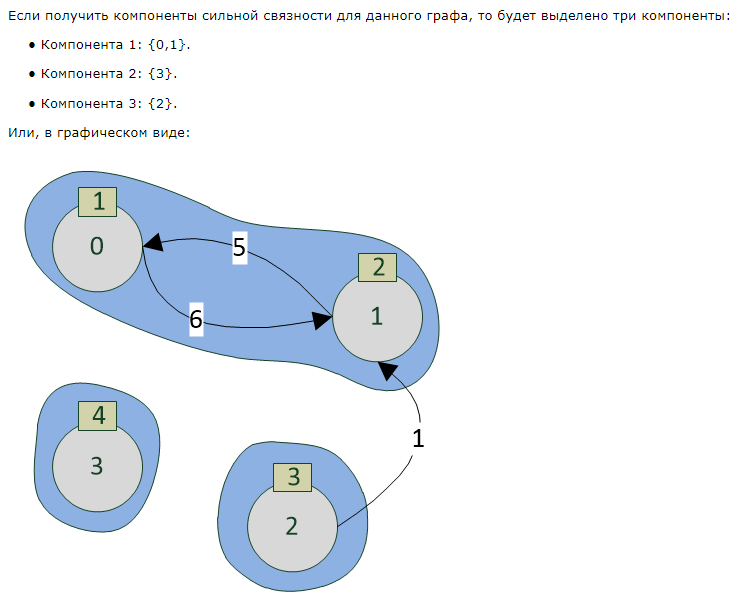
Далее мы попробовали механизм на живых данных. Согласно полученной выше матрице смежности указали в качестве колонки уравнения «ИдентификаторУзлаДт» и колонки переменной «ИдентификаторУзлаКт». Коэффициент в данном случае не важен, поэтому везде заполнили = 1.

Но, к сожалению, ни один из методов не дал внятных результатов. В режиме компонент сильной связности в результирующей таблице было достаточно много «шума» — компонент, которые на поверку оказывались не сильно связными. Поэтому пришлось отказаться от этого метода.

Но здесь следует учесть, что в тот момент разработка велась на версии платформы 8.3.17.1549 в режиме совместимости 8.3.12. Позднее мы проверили метод сильной связности на пилотном примере на более поздней версии платформы, ошибок найдено не было.

Ищем КСС с помощью библиотеки Python NetworkX

Ещё один механизм для поиска КСС который мы рассматривали — внешняя библиотека NetworkX (networkx.org) на языке Python.

Исследовали методы:

• Simple_cycles — find simple cycles (elementary circuits) of a directed graph.
  На рабочих данных метод возвращал миллионы циклов, что не поддавалось обработке.
• Strongly_connected_components — generate nodes in strongly connected components of graph.
  После ряда экспериментов в конечном итоге метод вернул достаточно малое количество КСС, самая большая из которых состояла из нескольких сотен узлов (при более чем 21 тысяче узлов в пилотном месяце), и с данной выборкой уже стало возможно работать.

Вычисление циклов внутри КСС в 1С и разрыв циклов для перехода к дереву

С полученным ограничением — в виде малого количества узлов в КСС — мы снова применили алгоритм на языке 1С по рекурсивному обходу ребер графа с вычислением циклов. Алгоритм представляет из себя классический поиск в глубину. При этом найденные циклы сразу же разрываются (об этом ниже) с периодической валидацией наличия КСС с помощью компоненты NetworkX в рамках нашего списка узлов.

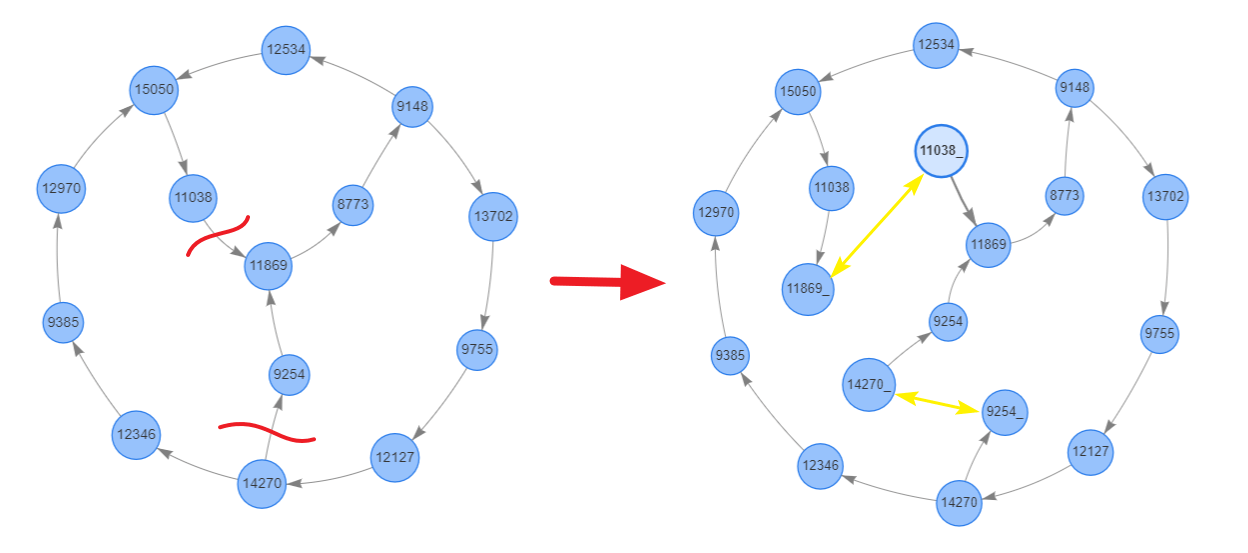
Основная идея разрыва цикла — заменить одно ребро из цепочки на два ребра с разделением идентификаторов узлов, чтобы они перестали быть связаны, при этом реальные аналитики (счет, подразделение, статья) по-прежнему остаются закрепленными за узлом.

Например, есть цикл, состоящий из ребер:

• A → B
• B → C
• C → A

Если мы выберем для разрыва ребро C → A, то после обработки получим такой набор:

• A → B
• B → C
• C → A1
• C1 → A

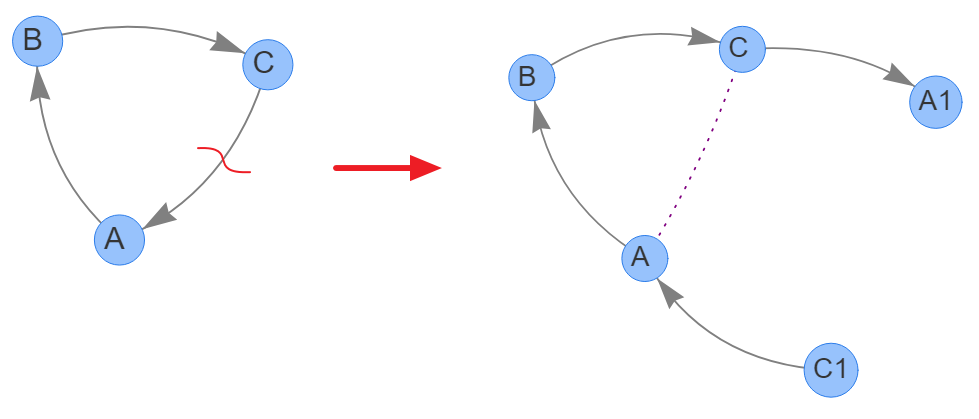
Также приводим пример сложнее, основанный на реальных данных:

Визуализируем графовые структуры в 1С

Иерархия в СКД

После разрыва циклов появилась возможность передать список ребер в СКД, т. к. попытка построить дерево в СКД при наличии циклов приводит к зависанию.

Система компоновки данных в 1С позволяет построить иерархию на основе таблицы смежности. Для этого нужно соединить набор данных этой таблицы с самим собой, указав в соединении ключевые поля родителя и дочерней строки. Похожую задачу мы рассматривали в прошлой статье.

В результате мы получили отчет в виде дерева подчиненных ребер.

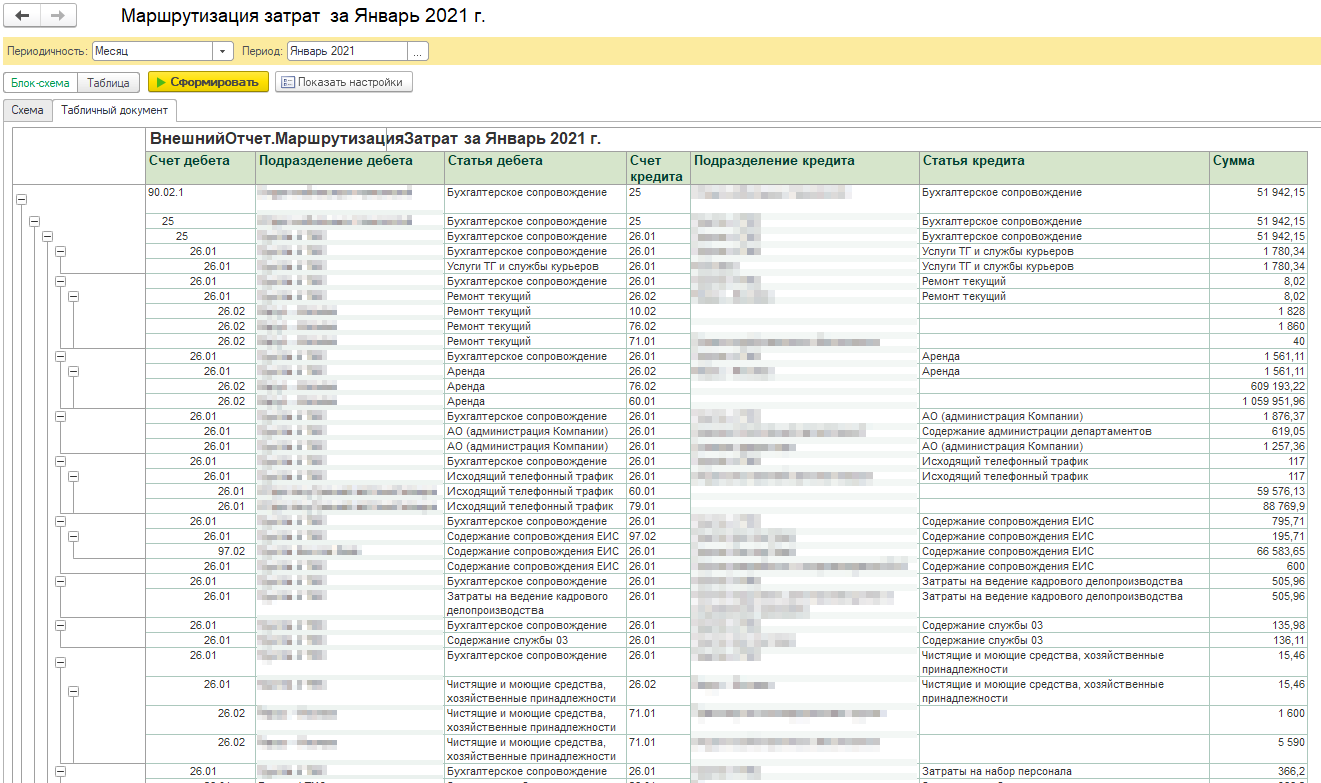
В целом, такая реализация вполне возможна и на ограниченных данных она заработала. Но в нашем случае обнаружилась проблема — даже при отборе всего одной ветви финреза (по одному подразделению и статье) — на нижнем листовом уровне такого дерева получалось настолько большое количество строк, что СКД не могла его вывести. По одному из пилотных отборов при входящем количестве ребер ~1 тыс. суммарно в построенном дереве было ~13 млн. строк.

Причина такого поведения в том, что из-за большого количества в сценарии операций агрегации и распределения при построении дерева одни и те же ребра нижнего уровня становятся подчиненными у многих родителей. Это приводит к множественному дублированию строк в дереве, причем с каждой такой парой шагов «агрегация/распределение» количество строк растет в геометрической прогрессии.

Таким образом, наш случай выходил за границы возможностей визуализации с помощью СКД. Пришлось отказаться от этого варианта и перейти к динамическому построению дерева значений.

Дерево значений

Дерево значений было выбрано по причине удобного построения и «отлавливания» события разворачивания группировки.

В качестве первичной выборки выводится 3 уровня вложенности дерева. В строках нижнего уровня вложенности взводится спец флаг, означающий, что по этим строкам далее может быть построена маршрутизация. Также в каждую такую строку добавляется дочерняя фиктивная строка для отображения значка группировки (+).

При раскрытии группировки пользователем, в событии «ПередРазворачиванием» делается запрос к базе и выводятся дочерние ребра с условием по вышестоящему:

ВЫБРАТЬ

  РебраГрафа.ПодразделениеДебета КАК ПодразделениеДебета,

  РебраГрафа.СтатьяДебета КАК СтатьяДебета,

  РебраГрафа.СчетДебета КАК СчетДебета,

  РебраГрафа.СчетКредита КАК СчетКредита,

  РебраГрафа.ПодразделениеКредита КАК ПодразделениеКредита,

  РебраГрафа.СтатьяКредита КАК СтатьяКредита,

  РебраГрафа.ИдентификаторУзлаДт КАК ИдентификаторУзлаДт,

  РебраГрафа.ИдентификаторУзлаКт КАК ИдентификаторУзлаКт,

  РебраГрафа.Сумма КАК Сумма

ИЗ

  РегистрСведений.МаршрутизацияЗатратРебраГрафа КАК РебраГрафа

ГДЕ

  РебраГрафа.Месяц МЕЖДУ &НачалоПериода И &КонецПериода

  И РебраГрафа.ИдентификаторУзлаДт = &ИдентификаторУзлаКт 

В результате получился такой отчет:

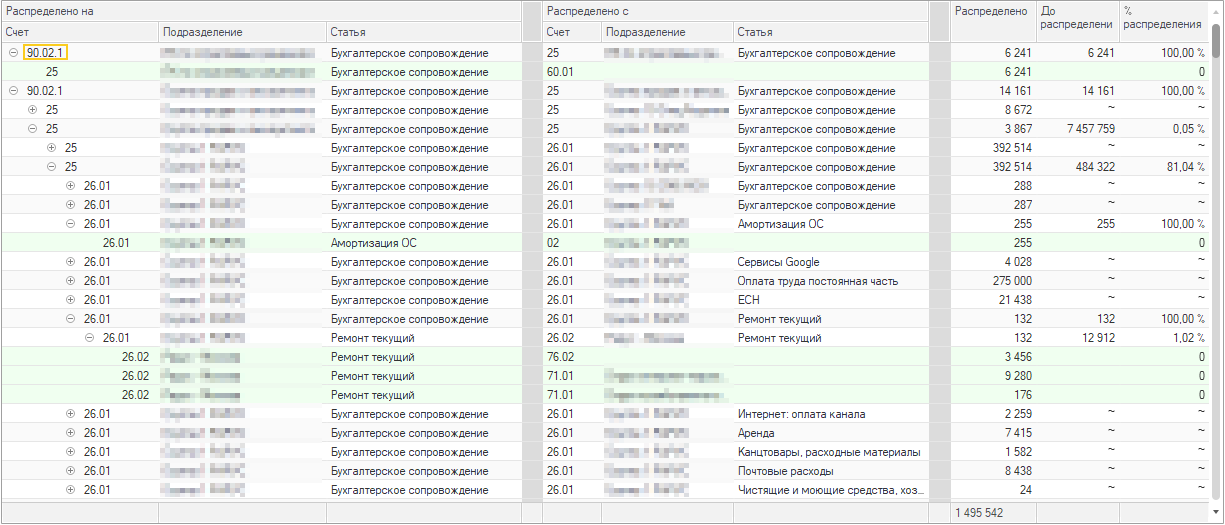
Такой подход избавляет от задачи поиска КСС. Нам уже не нужно убирать циклы в матрице смежности заранее, достаточно их вычислять динамически в момент получения очередной порции данных и прерывать цепочку.

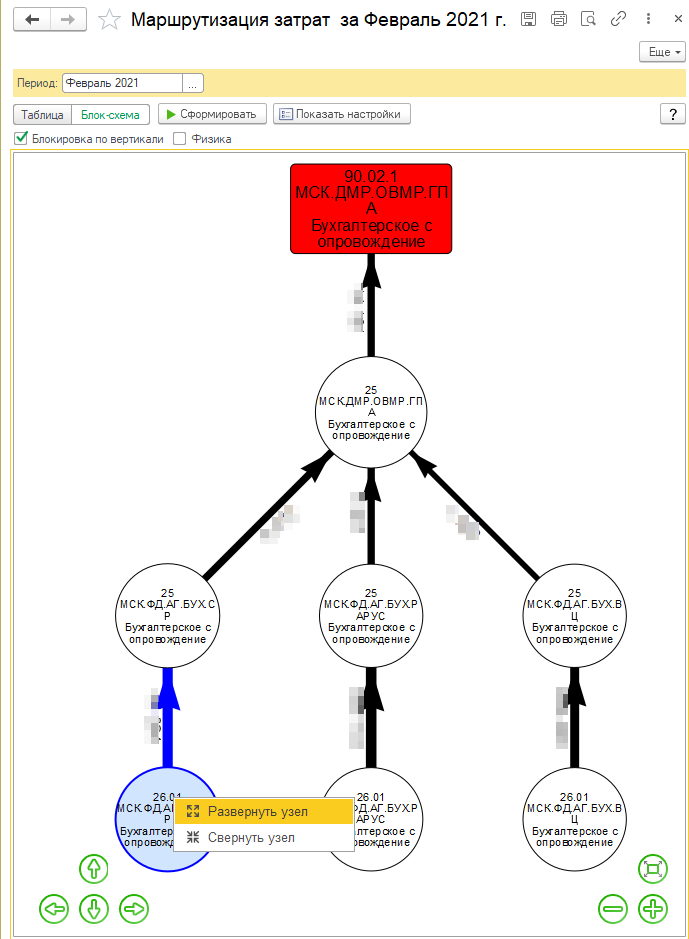
Блок-схема: HTML документ + библиотека vis.js

Чуть позже, для лучшего визуального восприятия, мы также с использованием сторонней библиотеки vis.js разработали дополнительный вариант отображения дерева в виде блок-схемы. Это достаточно мощный инструмент для визуализации различных сетевых структур. Мы разберем подробнее подходы в работе с библиотеками визуализации на javascript в следующей статье.

Выводы

Какие выводы можем сделать по результатам двух публикаций.

• Самый главный вывод состоит в том, что без знаний математики решать задачи такого класса невозможно. Можно пытаться это делать, но скорее всего такие решения станут работать только в частных случаях или будут работать медленно, при любом «чихе» будут вести себя неадекватно.
• Второй вывод состоит в том, что инструменты, которые «гарантируют» решение задачи или подзадачи могут иметь ограничения по размеру данных, с которыми вы имеете дело, либо и вовсе возвращать неверный результат.
• И третий вывод, не менее важный, в том, что даже если вам кажется, что задача «неподъемна», не опускайте руки. Как цитировал Никита Старичков в докладе на 1C-RarusTechDay 2021 девиз Физтеха — Sapere aude («Дерзай знать»).