От экспертов «1С-Рарус»: Введение в криптографию для специалистов по 1С. Теория, криптопровайдеры, использование электронных подписей

Цель статьи

Задачи по криптографии не самые распространенные в 1С. Тем не менее, такие вещи, как электронная подпись, все плотнее входят в нашу жизнь и периодически разработчикам 1С выпадает разбираться с какими-то вопросами из этой сферы.

Мы надеемся, что данный материал даст обзорное понимание, с чем может столкнуться специалист 1С в области криптографии, какие в ней присутствуют понятия, какие инструменты для работы у нас имеются.

Криптография вокруг нас

Области применения криптографии разнообразны. Это явное применение ее «по назначению»:

• хранения шифрованной конфиденциальной информации;
• электронная подпись, подтверждение подлинности;
• шпионские послания.

Применение, как один из вспомогательных элементов и составляющей более комплексных систем, протоколов, процессов:

• механизмы авторизации в различных интернет-сервисах;
• протоколы передачи данных (HTTPS, TLS, SSL);
• шифрование голосового трафика в сотовых сетях.

Масса вещей вокруг нас тоже содержит криптографию:

• данные в нашем телефоне или компьютере часто зашифрованы;
• сообщения в некоторых мессенджерах;
• информация на банковской карте;
• брелок сигнализации автомобиля.

Всего и не перечислить.

Множество механизмов и технологий используют криптографию неявно, глубоко в библиотеках, и мы не задумываемся, что это так, даже используя эти технологии.

Например, соединение по протоколу HTTPS и соответствующий объект 1С HTTPСоединение. Этот объект использует шифрование, но это происходит само по себе, без нашего участия. И не требует вмешательства и даже понимания, как это работает.

Иногда же возникают задачи, требующие более глубокого погружения в тему.

Сама криптография (как, в общем-то, следует из названия) — это наука о шифровании. Попросту говоря, шифрование занимается тем, что превращает понятные данные в непонятные, иногда с возможностью обратного действия, а иногда — с отсутствием такой возможности.

Немного истории вопроса

Первые методы шифрования были основаны на чисто физических объектах.

Скитала (сцитала)

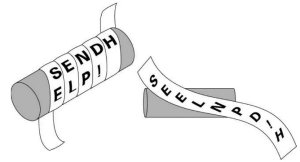
Представляет собой стержень, на который наматывается длинный, узкий (в ширину буквы) пергамент. Вдоль оси стержня записывается текст (в несколько рядов). После разматывания сообщение превращается в набор букв. Для расшифровки требуется стержень такого же диаметра.

Линейка Энея

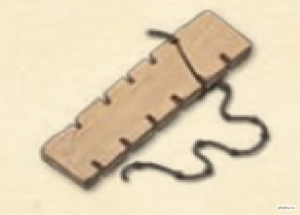
На линейку возле засечек нанесены буквы и имеется «нулевое» отверстие. Буква кодируется расстоянием между «нулевым» отверстием и соответствующей прорезью. То есть, нить протягивают между этими отверстиями и завязывают узелок, затем продевают обратно в «нулевое» отверстие и в прорезь следующей буквы. Последовательно на нити завязываются узелки для всего текста. Расстояния между узелками — коды букв. Обратная расшифровка требует такой же линейки, с такими же буквами.

Диск Энея

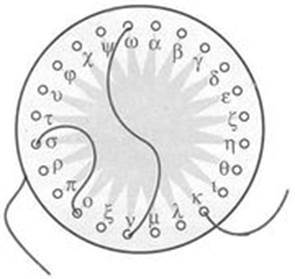
Диск имеет отверстия, каждое закодировано буквой. Нить просто последовательно продевается через буквы-отверстия, соответствующие тексту послания. Вытягивая нить обратно, восстанавливаем текст. Секретность состоит в том, что диск можно сломать или быстро вытащить нить и все — сообщение прочитано быть не может.

Решётка Кардано

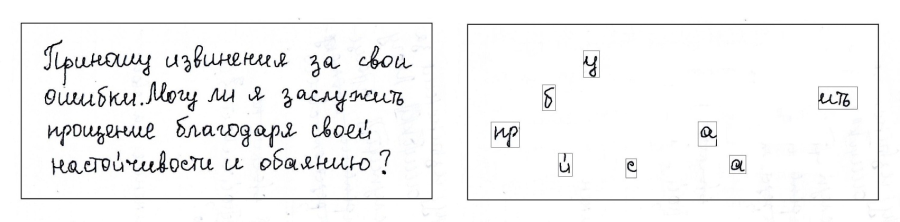
Послание прячется внутри внешне безобидного текста, для расшифровки требуется наложить на текст шаблон (решетку) с отверстиями и прочитать полученное.

В таких способах шифрования подразумевается, что и у отправителя, и у получателя сообщений есть одинакового вида приборы, по сути это древний пример симметричного шифрования. Ну, а ключом симметричного шифра в данном случае является, по сути, набор физических характеристик предмета, то есть геометрические размеры, расположение дырочек, засечек и т д. И для соблюдения секретности нужно держать в тайне сам предмет — инструмент шифрования.

Всем известная Энигма

Основа этой машины — шифры замены, когда алфавиту исходного текста сопоставляются другой набор символов и производится замена (как, к примеру, Шифр Цезаря).

Для каждой буквы сообщения Энигма выполняла последовательно несколько таких замен, при этом на каждой букве менялся сам шифр замены, то есть соответствие символов.

Способы шифрования без устройств

Другие способы шифрования заключались уже в некотором алгоритме по перестановке или замене букв, и здесь не было устройства, но необходимо было знать ключ. Например, Шифр Цезаря — для него требуется знать, на сколько символов мы сдвинули алфавит вправо или влево.

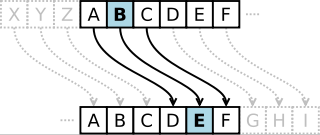
Шифр Цезаря

Символы алфавита с номером N заменяются на символы с номером N + k.

Атбаш

Буквы заменяются на симметричные им буквы с конца алфавита.

«Пляшущие человечки»

Нельзя не вспомнить шифр из произведения Конан-Дойля «Пляшущие человечки». Это простейший шифр замены (букв на пиктограммы)

Современные способы шифрования

Современная криптография не полагается на какие-то механические и физические устройства, а применяет исключительно математический аппарат для преобразования данных.

Физические устройства используются только в качестве вычислительных машин или защищённого хранилища для секретных ключей.

При этом, сами методы шифрования не держатся в секрете, как, например, физические механизмы, использовавшиеся когда-то. Алгоритмы свободно распространяются и вполне могут быть воспроизведены.

Но алгоритмы предполагают входные параметры, называемые ключами, и вся секретность как раз содержится в ключах, так как от использования правильного ключа зависит выходной результат того или иного вычисления.

Симметричное и асимметричное шифрование

Алгоритмы шифрования разделяют на два класса: с закрытым ключом (симметричное шифрование) и с открытым ключом (асимметричное).

При симметричном шифровании ключ один, он используется и для операции шифрования, и для расшифровки.

При асимметричном шифровании для этих двух операций используются разные ключи. Такие системы считаются более надежными, так как нет необходимости передавать тайный ключ собеседнику и тем самым подвергать ключ опасности раскрытия. Кроме того, система с открытым ключом, по сути, дает нам еще одну возможность — создавать электронную подпись. С другой стороны, асимметричное шифрование требует намного больше вычислительных ресурсов.

Несколько известных алгоритмов шифрования

Симметричные шифры

• XOR, шифр Вернама. Это, наверное, самый простой шифр. К каждому байту текста применяется операция XOR с соответствующим байтом ключа. Ключ имеет ту же длину, что и текст сообщения.
• RC4. В данном шифре используется XOR не с заранее заготовленным ключом, а с последовательностью псевдослучайных чисел. Сама последовательность генерируется на основе короткого закрытого ключа. Алгоритм генерации таков, что обе стороны получают одинаковый набор псевдослучайных чисел. Это позволяет на одной стороне зашифровать этими числами, а на другой такими же числами расшифровать. Передавать сами числа, то есть ключ, не требуется.
• DES — это устаревший стандарт шифрования США (Data Encryption Standard). С ростом производительности компьютеров, стала все более вероятна возможность вскрытия шифра обычным перебором или более сложной атакой, и он был заменен на AES.
• AES (Rijndael) — текущий стандарт шифрования в США. Интересно, что операции, требуемые для шифрования этим алгоритмом, встроены непосредственно в систему команд процессоров Intel x86 (расширение AES).

Асимметричные шифры

• На основе факторизации целых чисел:
• RSA.
• На основе дискретного логарифмирования:
• DSA,
• ГОСТ Р 34.10-94.
• На эллиптических кривых:
• ECDSA,
• ГОСТ Р 34.10-2012.

В основе надежности асимметричных шифров лежит сложность некоторых математических задач.

В алгоритме RSA, и подобных ему, это задачи факторизации, то есть разложения на простые множители больших чисел.

Перемножить два числа достаточно легко, при этом обратная задача является вычислительно сложной. С увеличением самих чисел становится практически невозможно выполнить ее за разумное время.

Одно из самых известных применений RSA — в криптографических протоколах, используемых в интернете — SSL и TLS.

В схеме Эль-Гамаля сложность состоит в получении значения дискретного логарифма в конечном поле. По этой схеме построены алгоритмы DSA, шифрование по стандарту ГОСТ Р 34.10-94.

Еще более стойкими к взлому считаются алгоритмы, основанные на сложности вычисления дискретного логарифма в группе точек эллиптической кривой (математические операции совершаются не над целыми числами, а над точками кривой). Такая схема используется в алгоритме ECDSA (по сути, это модификация DSA под эллиптические кривые). Кроме того, алгоритмы из последних стандартов ГОСТ построены на этой схеме (ГОСТ 2001, 2012, 2018).

Криптоанализ

Одновременно с криптографией появился и криптоанализ — наука о способах дешифровки зашифрованной информации, и вообще, о поиске уязвимостей в криптографической защите.

Например, самые простые атаки и способы взлома шифров замены заключаются в статистическом анализе шифротекста и сравнении результатов с закономерностями в языке, на котором написан исходный текст. Популярно об этом можно прочитать в уже упоминавшихся «Пляшущих человечках» (Артур Конан Дойль).

Используемые сейчас сложные шифры так легко не взламываются, криптографический инструментарий стал гораздо менее уязвим к атакам различного рода. Тем не менее, существуют различные методы криптоанализа, и иногда в тех или иных шифрах находят уязвимости.

Также, с развитием вычислительной техники и появлением распределенных вычислений, периодически становится актуальна защищенность методов шифрования от атак типа Brute Force, простым перебором значений. Именно поэтому важную роль играет длина ключа шифрования — чем длиннее ключ, тем больше вариантов надо перебрать.

Кроме того, существуют еще атаки с помощью социальной инженерии. Самым слабым звеном в защите часто является человек. Это тоже приходится учитывать при разработке криптографических методов.

Таким образом, каждый алгоритм имеет свой уровень стойкости к взлому, надёжности, безопасности.

Криптографические примитивы

Всё, о чем мы говорили выше, касается, в основном, шифрования.

В современной криптографии шифрование — это не только самоцель всего процесса, но и инструмент, который используется и для выполнения других операций (примитивов).

Каждый из этих примитивов также занимается превращением понятных данные в непонятные, но с разными целями и разными результатами. Обычно выделяется три таких операции-примитива.

Хеширование

Хеш-функция — это некая функция, которая позволяет из данных произвольного размера получить псевдо-уникальное значение определённой фиксированной длины. Это, можно сказать, тоже своего рода процедура шифрования (из понятных данные мы получаем непонятные), но она необратима, то есть из хеш-суммы обратно данные получить нельзя.

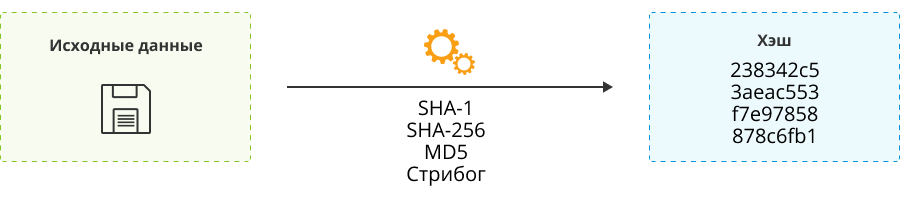
Бывают алгоритмы хэширования, так сказать, повседневные, знакомые всем:

• MD5,
• SHA256.

Также применяются более экзотические алгоритмы хэширования, например, в российских стандартах:

• ГОСТ Р 34.11-94,
• ГОСТ Р 34.11-2012 (этот алгоритм имеет собственное имя Стрибог).

Шифрование

Вторая криптографическая функция — это собственно шифрование. Обратная к ней — это расшифровка данных.

В этой операции уже задействовано такое понятие, как ключ — открытый и закрытый. Открытый ключ — это значение, которое свободно распространяется и открыто для всех.

Закрытый ключ — это секретное значение которое владелец держит в тайне.

Шифрование происходит с использованием открытого ключа, На выходе мы получаем шифротекст.

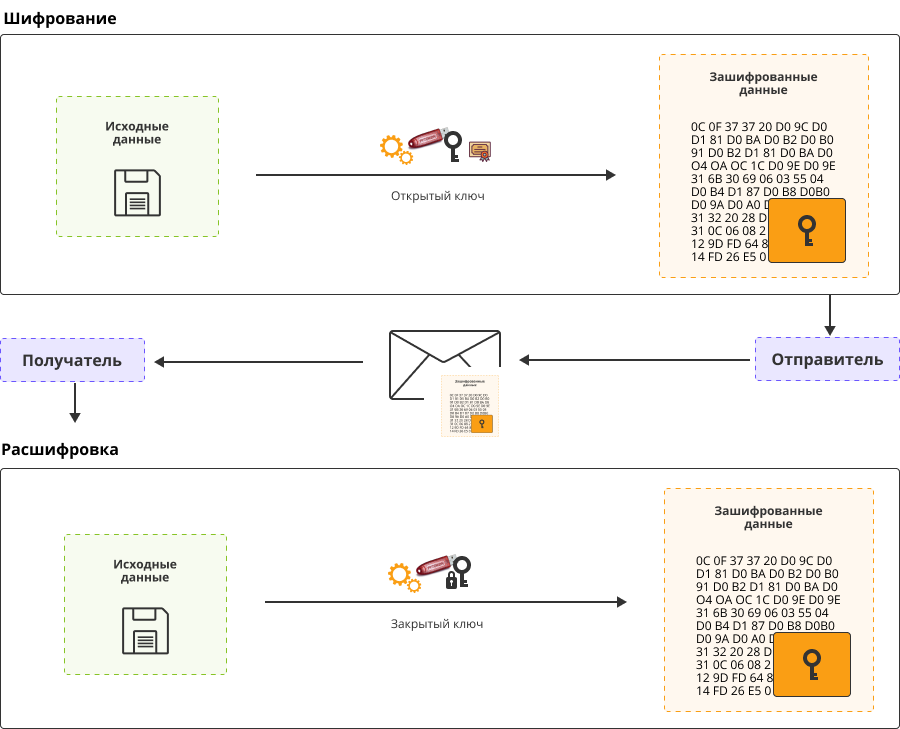
Расшифровка выполняется при помощи закрытого ключа.

Есть распространенное заблуждение, что все как раз наоборот, и для шифрования используется закрытый секретный ключ. Это так, для симметричных шифров. В них открытый и закрытый ключ совпадают, используется всего один ключ, который известен и получателю и отправителю и они, конечно, держат его в секрете.

При асимметричном шифровании схема работает приблизительно так:

• Если мы хотим получать от наших корреспондентов зашифрованную информацию, мы генерируем ключевую пару и распространяем открытый ключ.
• Этим открытым ключом для нас будут шифровать информацию. При этом расшифровать открытым ключом нельзя — это односторонняя операция.
• Но расшифровать можем мы, при помощи своего закрытого ключа. В этом и есть секретность — закрытый ключ известен только владельцу.

Мы уже говорили ранее, что асимметричное шифрование — это медленная операция. Поэтому на практике часто шифрование, в особенности больших или потоковых данных происходит так:

• Генерируется ключ для симметричного шифра — «сеансовый ключ».
• Ключ зашифровывается открытым ключом асимметричного шифра.
• Зашифрованный ключ передается второму участнику взаимодействия.
• Второй участник расшифровывает симметричный ключ.
• Теперь у каждого участника обмена есть ключ для симметричного шифра, переданный безопасным способом.
• Дальнейший обмен происходит при помощи симметричного шифрования.

Как вариант, при передаче пакета данных в него сразу помещается:

• Ключ симметричного шифра (сеансовый), зашифрованный асимметричным.
• Данные, зашифрованные симметричным шифром, сеансовым ключом.

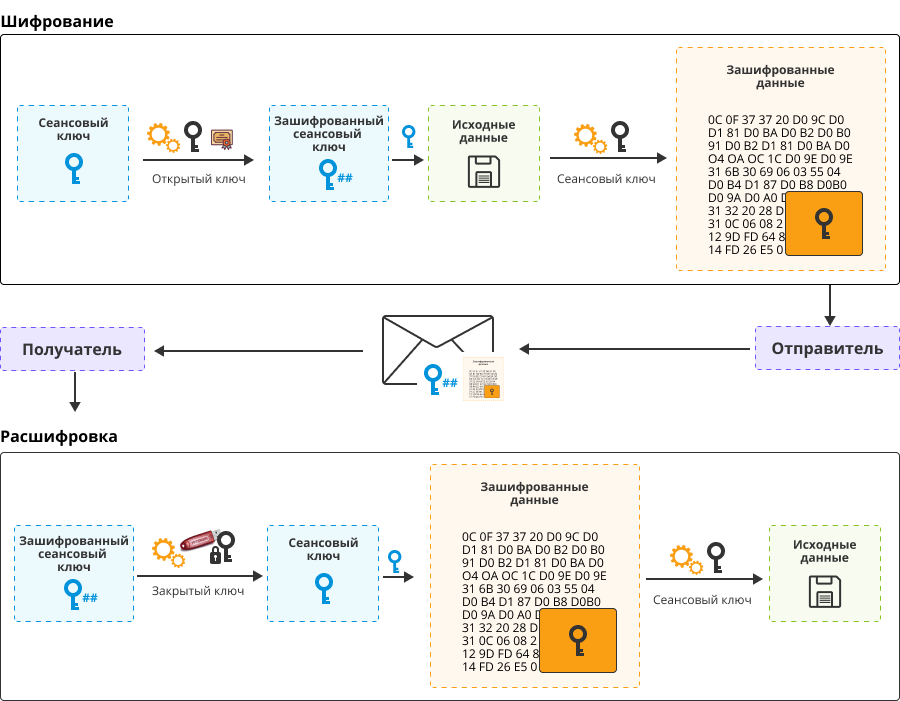
Результат шифрования, полученный при помощи платформы 1С, устроен как раз таким образом.

Эта схема позволяет выполнять «дорогостоящее» асимметричное шифрование на небольшом значении сеансового ключа. А большой объём передаваемых данных — зашифровывать быстрым симметричным шифром.

Электронная подпись

Электронная подпись создается с использованием закрытого ключа. Закрытый ключ известен только владельцу подписи, соответственно, только он может создать эту подпись. Для этого исходные данные и закрытый ключ передаются в функцию вычисления подписи, на выходе получаем некое новое значение, которое называется «подпись» или «значение подписи».

Это небольшое значение, например 512 бит. Иногда его называют «сырое» значение электронной подписи — то есть, не завернутое ни в какие обертки или форматы, просто результат вычисления математической криптографической функции.

Электронная подпись — это тоже своего рода шифрование. Из понятных входных данных мы получаем непонятное значение подписи.

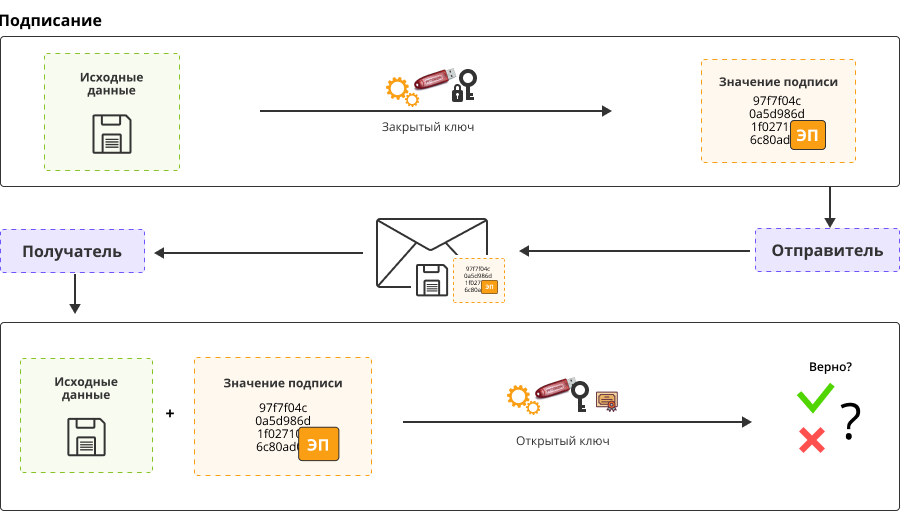
Обратная задача состоит в том, чтобы убедиться, что исходные данные соответствуют значению подписи. Два этих значения передаются в криптографическую функцию, и при помощи открытого ключа проверяется, соответствуют ли эти данные — этой подписи.

Открытый ключ надо где-то заранее получить, часто он вкладывается в тот же пакет, что и остальные значения.

Отметим такой момент, что электронная подпись никоим образом не шифрует информацию. И не предназначена для скрытия или шифрования информации. Значение подписи вообще не содержит исходных данных — это некое дополнительное значение.

Чтобы передать получателю подписанные данные, мы помещаем в один пакет сами исходные данные и значение подписи. Исходные данные при этом не шифруются..

Если же требуется засекретить информацию, надо дополнительно использовать шифрование, и это будет уже более сложная операция.

Часто при установке электронной подписи к данным в один пакет добавляют также дополнительные сведения для большей защищенности. Например дату подписания, имя субъекта, который подписал и прочую информацию.

Все это объединяется в одну общую структуру информации, а затем уже устанавливается подпись на полный объем данных. Таким образом, например, если кто-то подложит исходные истинные данные, но подменит дату подписи, это можно будет установить.

Как и при шифровании, в случае большого объема данных установка подписи является достаточно затратной вычислительной операцией. Поэтому часто также применяется методика для уменьшения этих вычислительных затрат.

Подпись устанавливается не на исходные данные или [исходные данные + дополнительные сведения], а на хеш этого значения.

Хеш считается (относительно) быстро, а посчитать подпись от нескольких байт значения хеша гораздо менее затратно, чем от большого блока исходных данных, теоретически ничем не ограниченных.

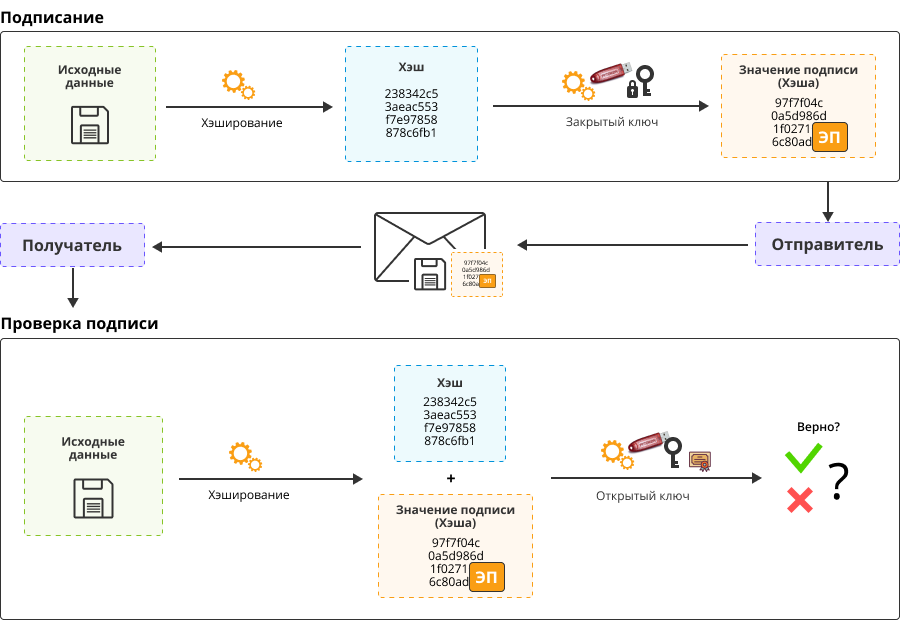
Электронная подпись даёт нам несколько полезных возможностей:

• Мы всегда можем проверить соответствие исходных данных значению подписи. И таким образом убедиться, что исходные данные верны и целостны.
• Мы всегда можем проверить, что именно этот владелец подписи подписал исходные данные. То есть убедиться в том, что данные заверены именно нужным субъектом.
• Также, так как только владелец подписи может её создать, наличие подписи удостоверяет, что именно он создал или заверил исходные данные. То есть владелец подписи не может отказаться от авторства.
• Используя более сложные форматы подписи, мы можем также удостоверять различные свойства исходных данных, такие, как, например, дата подписания документа.

Виды электронной подписи в России

Существует, в соответствии с российским законодательством, три вида электронной подписи:

• простая,
• усиленная неквалифицированная,
• усиленная квалифицированная.

Простая подпись — это, например, SMS-код. Криптография не используется.

Усиленная неквалифицированная (УНЭП) — создается при помощи криптографических средств. Такая подпись генерируется и действует внутри какой-то системы. Например, это может быть внутренний документооборот компании. Также, этот вид подписи выпускается для желающих физлиц в личном кабинете налогоплательщика. Теоретически, может использоваться любое программное обеспечение.

Усиленная квалифицированная (УКЭП) — тоже создается при помощи криптографических средств, но используемые средства и алгоритмы должны быть сертифицированы ФСБ.

Таким образом, в теории, в некоторых случаях можно использовать УНЭП. На практике, почти все системы взаимодействия и интеграции, в особенности государственные, требуют использования УКЭП. По сути, это сужает выбор из всего разнообразия алгоритмов до алгоритмов, определенных стандартами ГОСТ (сейчас — ГОСТ 2012), а программного обеспечения — до имеющих соответствующую регистрацию и сертификацию.

Криптопровайдеры

Как мы выяснили, для работы с криптографическими инструментами нужно иметь математический аппарат (алгоритмы), набор криптографических функций для преобразования данных. Некоторые из них мы уже перечислили выше. Алгоритмов существует множество, они различаются назначением, сложностью, стойкостью к различным атакам.

Криптография не стоит на месте. Какие-то алгоритмы считаются устаревшими или небезопасными и уже не используются.

Иногда появляются новые модификации алгоритмов. Например, алгоритмы, закрепленные ГОСТ, менялись несколько раз: ГОСТ Р34.10-94 сменился на версию ГОСТ 2001, а несколько лет назад происходил массовый переход систем на ГОСТ 2012. При этом менялись не просто названия, а существенные характеристики алгоритмов.

Для того, чтобы практически выполнять какое-то шифрование не требуется реализовывать заново алгоритм на каком-либо языке программирования. Для этого предназначены готовые программные продукты — СКЗИ (средства криптографической защиты информации), или криптопровайдеры.

Программ-криптопровайдеров существует немало, вот несколько из них:

• Microsoft Base Cryptographic Provider,
• Крипто Про,
• Vipnet,
• Сигнал-Ком,
• Код безопасности.

Разные криптопровайдеры умеет исполнять разные наборы алгоритмов криптографии. Некоторые простые алгоритмы встроены в операционную систему, например, в системе Windows есть Microsoft Base Cryptographic Provider. Он используется для различных внутренних криптографических потребностей системы, таких как: шифрование и хеширование паролей, поддержка протоколов SSL и TLS.

Но те алгоритмы, которые нам обычно интересны, например, все тот же ГОСТ, в операционной системе отсутствует и для них нужно использовать дополнительные программы.

В нашей практике двумя самыми распространёнными криптопровайдерами являются КриптоПро и VipNet.

Криптопровайдеры — капризные программы, с ними иногда бывают трудности. Установленные на одной операционной системе криптопровайдеры часто конфликтуют между собой. Также есть случаи конфликтов с антивирусами. Отмечались случаи, когда возникали проблемы с подключением к сети на компьютере.

Также, в документации 1С (its.1c.ru/db/v83doc#bookmark:dev:TI000000835) прямо написано, что в Linux с 1С работает СКЗИ КриптоПро. По сути, мы ограничены одним программным продуктом. Другие программы не упоминается и, соответственно, не поддерживаются.

Инициализация криптографии в 1С

Для использования криптографии в 1С у нас есть не так много инструментов — их всего два. Это менеджер криптографии и внешняя компонента XMLDSig.

Менеджер криптографии — это объект встроенного языка 1С.

Сам он не выполняет криптографических операций, а вызывает функции установленных в системе библиотек криптопровайдеров посредством интерфейса — CryptoAPI.

Внешняя компонента XMLDSig — второй инструмент, это внешняя компонента для платформы 1С, она включается в поставку БСП. В новой версии БСП появилась новая версия этой компоненты с несколько дополненными возможностями, она называется ExtraCryptoAPI.

Эта библиотека несколько расширяет возможности менеджера криптографии.

В БСП в модулях подсистемы электронно-цифровой подписи реализованы основные необходимые функции-обертки для работы с этой компонентой.

Для того, чтобы начать работу с объектом МенеджерКриптографии, его надо инициализировать. Здесь приведен пример кода.

В этом фрагменте можно заметить некоторые константы, которые здесь обозначены ИмяМодуля, ТипМодуля, АлгоритмПодписи и т. д.

Это достаточно важные значения. ИмяМодуля + ТипМодуля задают нам криптопровайдер, который мы хотим вызвать через API операционной системы Windows.

А вот ПутьМодуля — предназначен для инициализации криптографии в системе Linux, где доступ к криптопровайдеру происходит не через системный вызов специального API, а через загрузку библиотек, пути к которым и нужно прописать в этой переменной.

АлгоритмХеширования и АлгоритмПодписи — задают выбранные алгоритмы для последующего выполнения.

Значения всех этих констант не просто произвольны, а зафиксированы для каждого криптопровайдера. Заметим также, что один и тот же алгоритм может в разных СКЗИ иметь разные наименования.

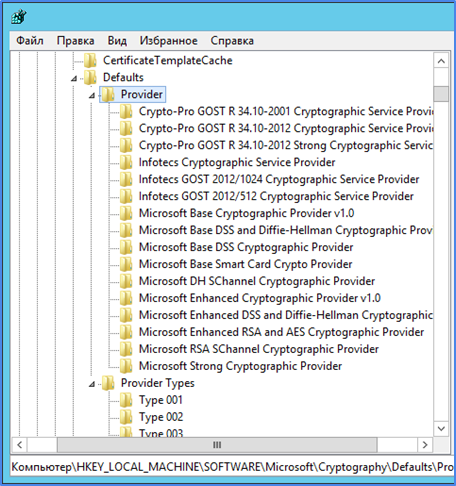
Возможные значения можно посмотреть:

• В документации к программному обеспечению (криптопровайдеру).
• В интернете.
• В исходных модулях БСП.
• Некоторую информацию можно найти в реестре Windows.
• В Linux можно воспользоваться утилитой cpconfig (утилита из состава продукта Крипто Про).

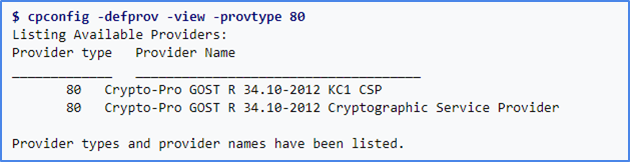
После инициализации у нас есть Менеджер криптографии — это объект, через который мы будем взаимодействовать с криптопровайдером и выполнять такие функции, как:

• Вычисление/выполнение криптографических примитивов: шифрование, электронная подпись.
• Взаимодействие с хранилищем сертификатов, установку сертификатов, получение информации о сертификатах, извлечение их из системы.

Также, для подписи и шифрования/расшифровки нам понадобится использовать ключи — открытый и закрытый.

Установка, хранение и связь ключей, сертификаты, контейнеры

Как уже сказано ранее, открытый ключ распространяется среди тех, с кем мы хотим взаимодействовать. Сам по себе открытый ключ — это большое число, чаще всего представленное в виде HEX-строки. Но распространяются ключи не как строка, а в виде сертификатов.

Сертификаты

Сертификат — это некий файл, который содержит, помимо самого открытого ключа, различные сведения об электронной подписи. Сертификат по сути — некий паспорт электронной подписи. Он, в свою очередь, тоже подписан электронной подписью — выпускающего удостоверяющего центра. Сертификат также подтверждает, что данный открытый ключ принадлежит именно нам, то есть конкретной организации или физическому лицу.

Файлы, содержащие сертификаты, часто имеют расширение CER или PFX. Если в проводнике Windows в такой файл щелкнуть, он откроется и будет выглядеть, как на картинке.

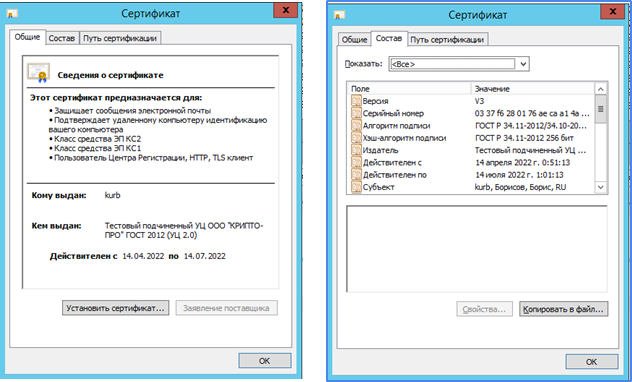
В этом окне можно просмотреть разные свойства электронной подписи. Здесь же можно заметить кнопку «Установить сертификат». Она позволяет поместить сертификат в специальное хранилище сертификатов и он будет «известен» системе.

Конечно, сертификат может просто располагаться в файле и при различных интерактивных и программных манипуляциях мы можем его выбирать или указывать к нему путь, как к физическому файлу.

Но в операционной системе предусмотрено централизованное хранилище сертификатов. Интерактивно, с помощью консольных утилит или программно, мы можем установить сертификат в хранилище.

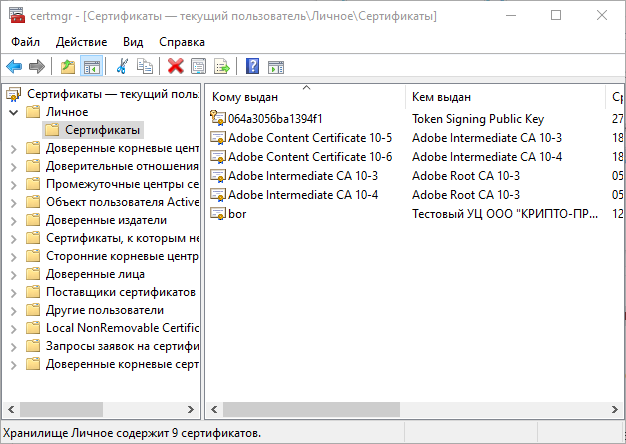
Для Windows при этом мы выбираем куда поместить сертификат: в хранилище компьютера, то есть доступно для многих пользователей, или в хранилище конкретного текущего пользователя.

Сертификаты делятся на категории: Личное, Корневые сертификаты удостоверяющих центров и несколько других категорий.

Система и криптопровайдер строят из этих сертификатов цепочки (когда сертификат пользователя, например, подтверждается сертификатом удостоверяющего центра), проверяет их целостность, сроки действия и т. д.

Закрытый ключ

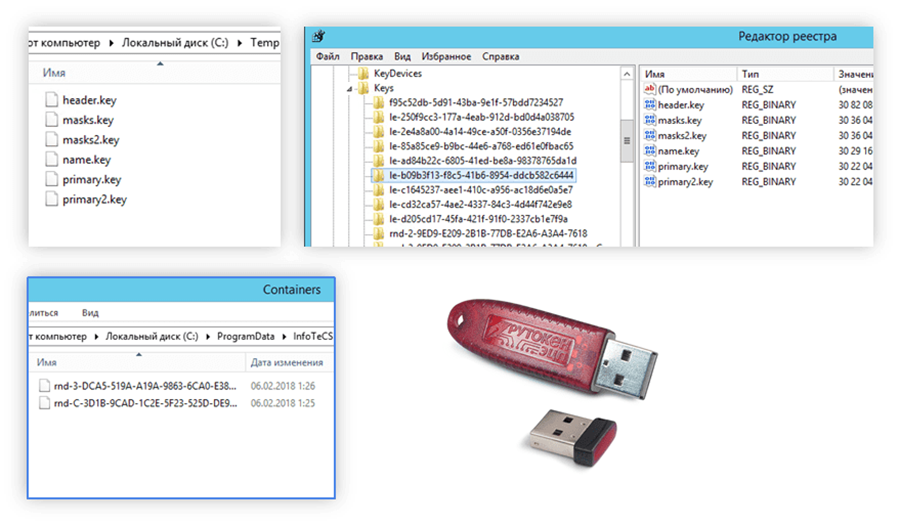
Закрытые ключи хранятся в «контейнерах». Контейнер может располагаться: в файловой системе (на флешке, на дискете), на смарт-карте, на аппаратном носителе-токене, в реестре Windows и даже в облаке.

Некоторые аппаратные носители не просто хранят в себе закрытые ключи, но являются более сложными устройствами и могут сами выполнять какие-то криптографические операции.

Контейнер закрытого ключа иногда можно перемещать между разными хранилищами. Например, ключ с аппаратного носителя можно скопировать в реестр Windows, чтобы каждый раз не требовалось вставлять носитель в USB-порт. Это, конечно удобно, но есть отдельный вопрос относительно безопасности такого решения.

Варианты контейнеров, их расположение, возможность перемещения, экспорта, импорта закрытых ключей определяется уже конкретным криптопровайдером. Дополнительно, контейнер закрытого ключа обычно защищается паролем.

Связь ключей и криптопровайдера

Если мы хотим воспользоваться электронной подписью и подписывать документы, нам необходимо в системе иметь три элемента: два ключа и криптопровайдер, а также установить между ними связь.

Необходимо, чтобы система знала: данный открытый ключ связан с данным контейнером закрытого ключа и с данным криптопровайдером.

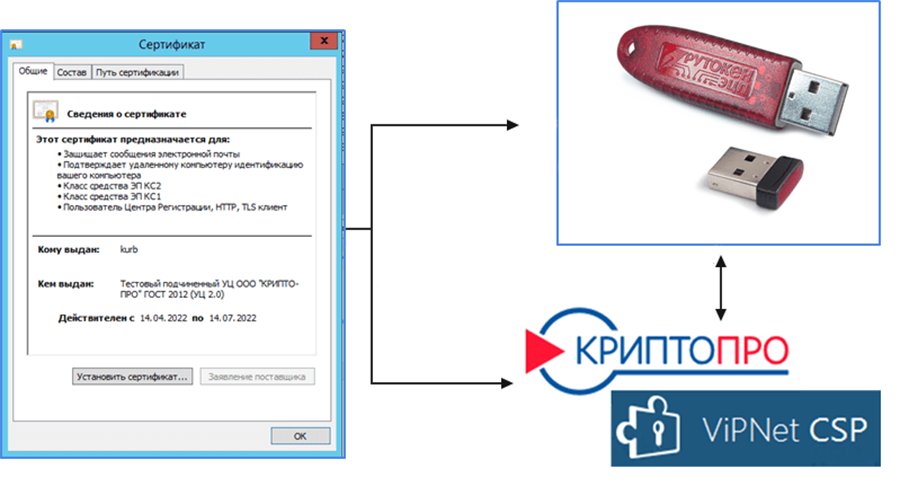
При этом, если для установки сертификата воспользоваться кнопкой «Установить сертификат», то такая связь не устанавливается и электронная подпись работает не будет. Для корректной установки сертификата и установления связи между сертификатом открытого ключа и контейнером закрытого ключа обычно выполняется их одновременная установка в систему, при помощи функции криптопровайдера.

Также, криптопровайдер может иметь функцию добавления связи для уже установленных ключей.

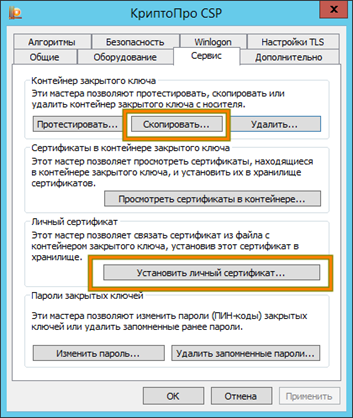
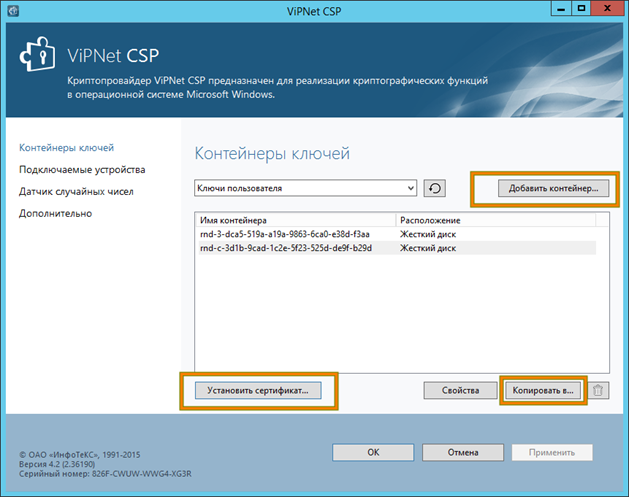
Некорректная установка подписи (ключей) в систему — одна из частых ошибок при настройке криптографии, при этом могут возникать самые разнообразные ошибки, вот только некоторые из них:

Сертификаты в коде 1С

Для того, чтобы воспользоваться закрытым ключом и что-то подписать или расшифровать данные непосредственно контейнер закрытого ключа не указывают. Используется сертификат открытого ключа, связанный с контейнером.

Для того, чтобы как-то взаимодействовать с открытым ключом, тоже используется сертификат открытого ключа.

Таким образом, для того чтобы выполнить какую-то криптографическую операцию связанную с ключами, нам необходимо указать сертификат.

Сертификатов в системе может быть несколько, так что, для выбора конкретного сертификата, нужно его как-то идентифицировать. У сертификата есть множество параметров, например: издатель, субъект (то есть, владелец), срок действия. Но все эти параметры не подходят в качестве идентификатора. Обычно для идентификации сертификата используется его поле «Отпечаток». Вообще, отпечаток — это просто хеш-сумма файла сертификата, но оно часто используется как его идентификатор.

В коде 1С чаще всего можно увидеть именно такой вариант.

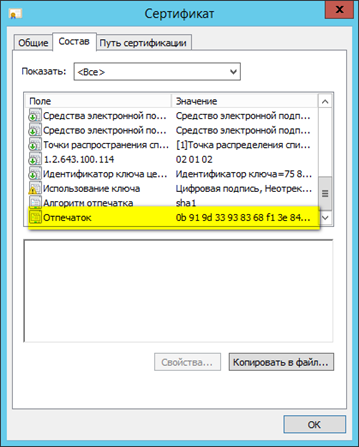
Для получения сертификата нужно воспользоваться менеджером криптографии, указав при этом из какого хранилища (общего для компьютера или персонального) мы хотим его получить.

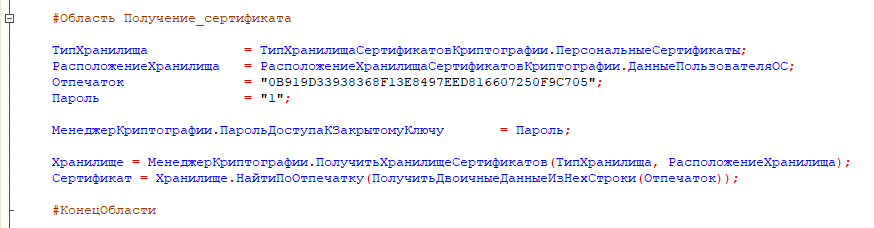
Так как закрытый ключ защищен паролем, для выполнения криптографических операций его тоже нужно указать.

 В приведенном примере пароль указан в явном виде исключительно в демонстрационных целях.

Также, с помощью менеджера криптографии можно выполнять и другие операции с сертификатами — перебирать, сохранять в файл, удалять из хранилища и т. д.

Стандарты, форматы

Когда специалист погружается в мир криптографии, он сразу сталкивается с огромным количеством различных аббревиатур и обозначений, помимо названий алгоритмов шифрования:

• ASN.1,
• CMS,
• XMLDSig,
• CAdES, JAdES, PAdES, XadES,
• PKCS#7, PKCS#10,
• CER/DER/BER,
• X.509.

В первый момент здесь легко потеряться. Попробуем, просто для ясности, разобрать что к чему относится.

PKCS#NN — это стандарты (Public Key Cryptography Standards), разработанные компанией RSA Security. Стандарты описывают самые разнообразные вещи, от алгоритмов шифрования до протоколов защищённого обмена и механизмов хранения и передачи криптографической информации. В частности, PKCS#7 (Cryptographic Message Syntax Standard) — стандарт хранения криптографических данных (сертификатов, подписей, шифрованных данных).

CMS, XMLDsig, CAdES, JAdES, PAdES, XAdES — это различные форматы хранения подписей и другой криптографической информации, например, сертификатов. Они описывают достаточно высокоуровневую структуру как и какие данные должны быть представлены внутри файла или потоковых данных с подписью или другой информацией.

ASN.1 — бинарный, низкоуровневый формат для хранения криптографических данных. Описывает побайтовую структуру файла.

CER/DER/BER — это форматы хранения сертификатов ключей электронной подписи и шифрования. Они приблизительно одинаковы, отличаются незначительными особенностями вроде способа кодирования внутренних значений и ограничениями на содержимое.

X.509 — обычно понимается как стандарт структуры сертификата.

Некоторые форматы подписи можно создавать из встроенного языка 1С.

Формат CMS/CAdES

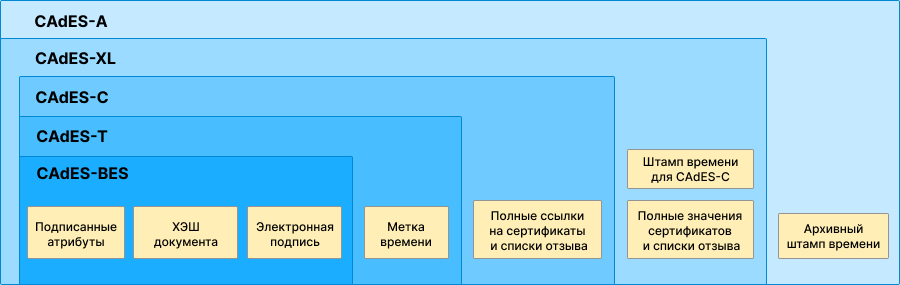
Одним из самых распространённых форматов является формат CMS. CMS — базовый формат. На его основе составлена целая гроздь форматов CAdES.

• CadES-BES,
• CadES-T,
• CadES-C,
• CadES-X,
• CAdES-X Long (CadES-XL),
• CadES-A,
• CAdES-A v2,
• CadES-LT,
• CAdES-A v3.

CMS — это определенная структура, которая содержит внутри значение электронной подписи и множество дополнительных атрибутов этой электронной подписи. Разные форматы CAdES — это разные варианты CMS, отличающиеся набором этих атрибутов.

Файлы, имеющие логическую структуру CMS физически сохраняются в бинарном формате на базе формата ASN.1. Вот пример такого файла в HEX-редакторе и структура, которую он содержит:

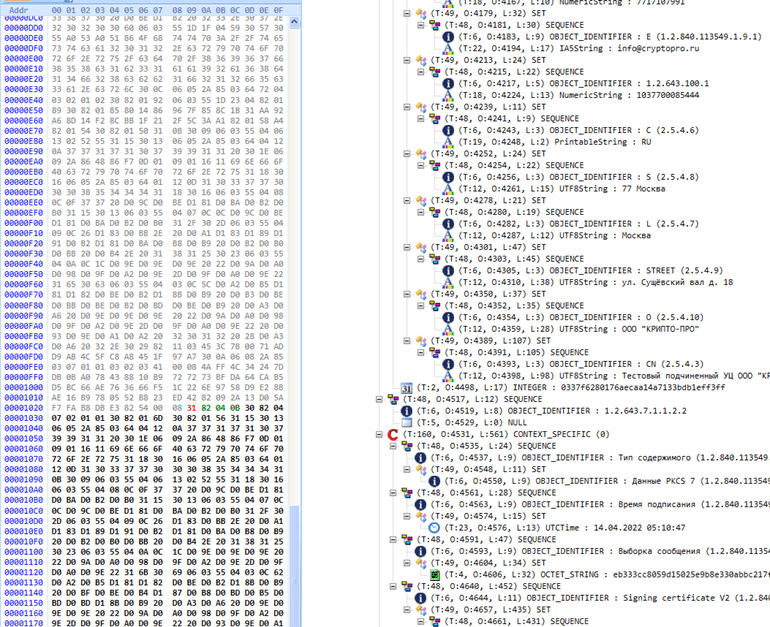
Здесь расположено множество атрибутов подписи, такие как:

• время подписания;
• сертификат, которым подписано;
• хеш данных;
• алгоритмы, использованные при подписи;
• и многое другое.

Сама же подпись занимает совсем небольшую часть файла:

CMS в коде 1С

Для создания подписи в программном коде 1С, можно воспользоваться объектом МенеджерКриптографии. Сначала инициализируем криптопровайдер, находим сертификат (фрагменты кода приведены ранее). Затем читаем данные из файла, который хотим подписать и передаем их в метод МенеджерКриптографии Подписать(). Кроме данных для подписи передаем сертификат подписи, которым хотим воспользоваться. Если все параметры корректны, на выходе мы получим подпись и запишем ее в файл.

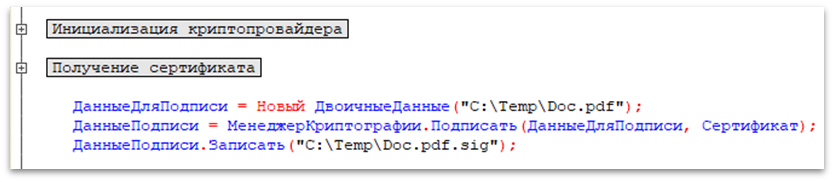
В последних версиях платформы (8.3.21...) появилась возможность указать, какой из форматов CAdES-* требуется получить. То есть можно получить подпись именно того формата, который требуется по условиям задачи. Например, можно создать подпись CAdES-T. Для этого, заметим, требуется указать адрес сервера для получения метки времени, которая включается в состав подписи.

Проверка подписи выполняется также при помощи менеджера криптографии. В случае неверной подписи генерируется исключение.

Подпись PDF

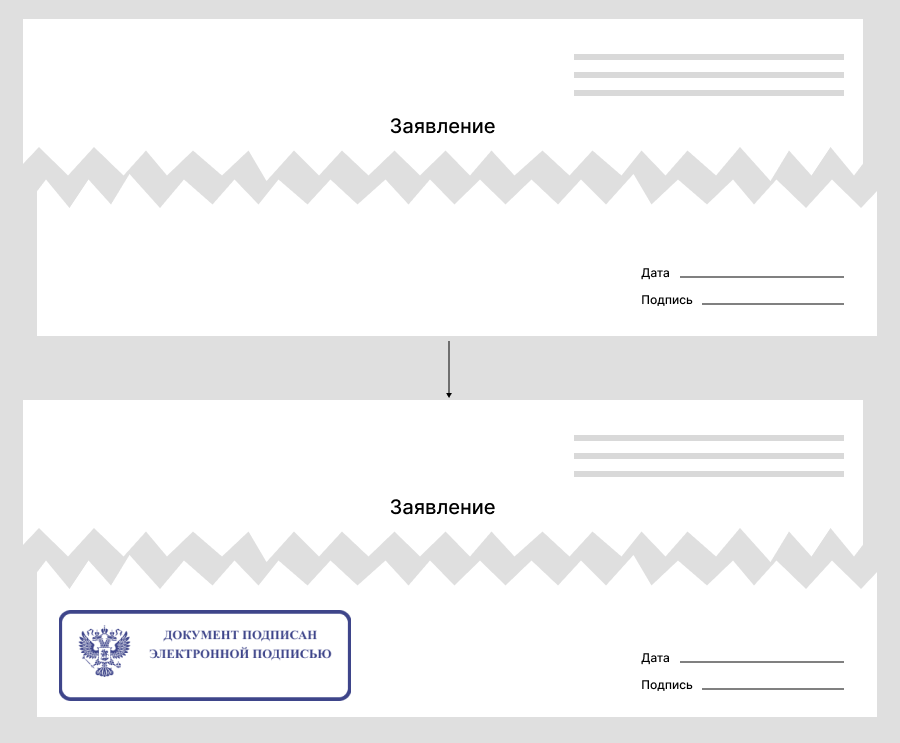
Платформа 1С позволяет подписывать файлы PDF электронной подписью.

Это внедренная подпись, она содержится внутри самого подписываемого документа, а не в отдельном файле, как в предыдущем случае.

Для создания PDF в платформе есть объект под названием ЗаписьPDF. В 16-ой версии платформы в нем появилась функция ЗаписатьПодпись(), которая позволяет в файл поместить электронную подпись, параметры которой заготовлены заранее.

Приведенный код вызовет криптопровайдер, вычислит подпись документа PDF, используя указанный сертификат, и поместит ее внутрь этого же документа в соответствии с форматом PDF. Дополнительно можно разместить картинку-штамп подписи.

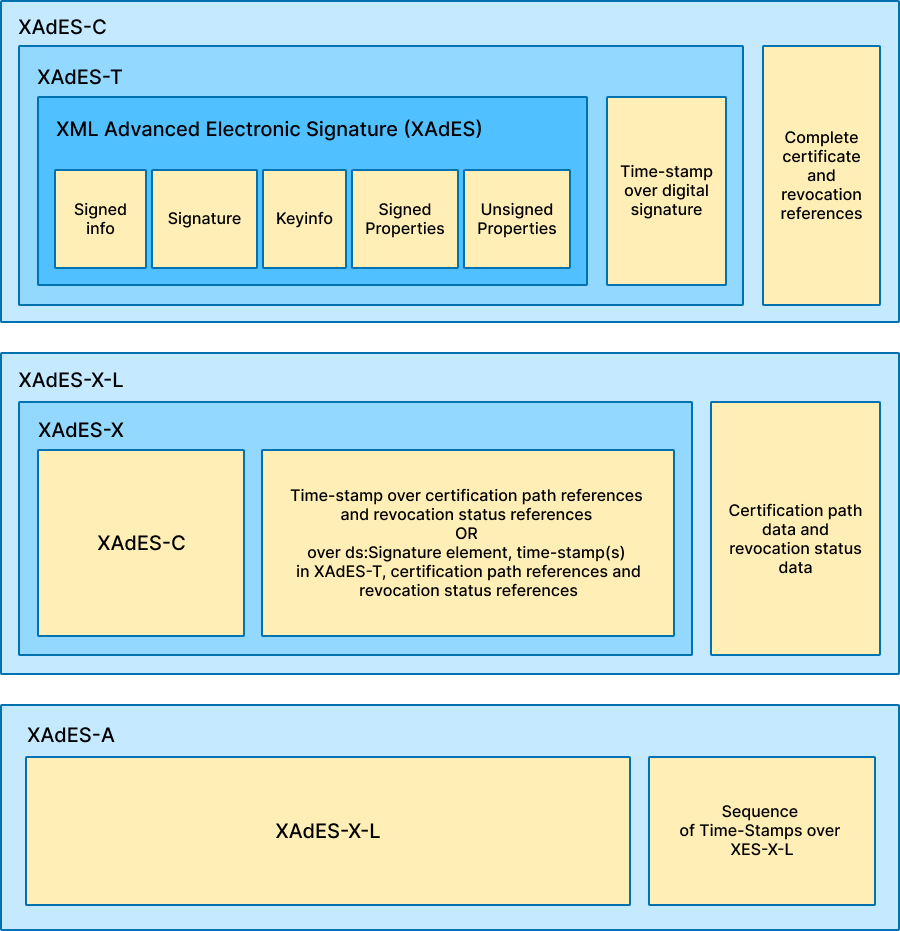
Формат XMLDSig/XAdES

XMLDSig и XadES — это тоже целое семейство форматов. Логика здесь приблизительно такая же, как с форматами CMS и CAdES — разные форматы XAdES содержат разное количество атрибутов, а базовым форматом является XMLDSig.

Для разработчика 1С это более сложный формат, чем ранее рассмотренные. Он доставляет гораздо больше неприятностей, потому что в отличие от ранее описанных форматов его нельзя просто так получить в одну-две строчки кода. Получение этой подписи — целый процесс.

Прежде всего, XMLDSig — это стандарт для подписи XML документов, например, сообщений веб-сервисов, передаваемых по протоколу SOAP. Подпись может быть внедренной или отделенной, то есть располагаться внутри, рядом или отдельно от подписываемых данных.

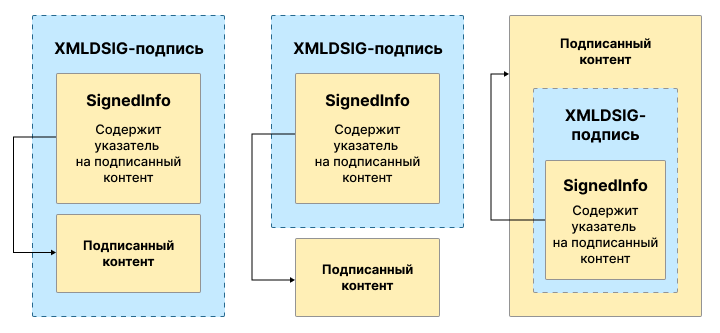
Чаще всего это внедренная подпись, то есть содержится в том же XML документе, что и подписываемые данные.

Сведения об электронной подписи могут располагаться в разных частях XML документа. В случае, если это SOAP сообщение, часто для этого используют блок Header.

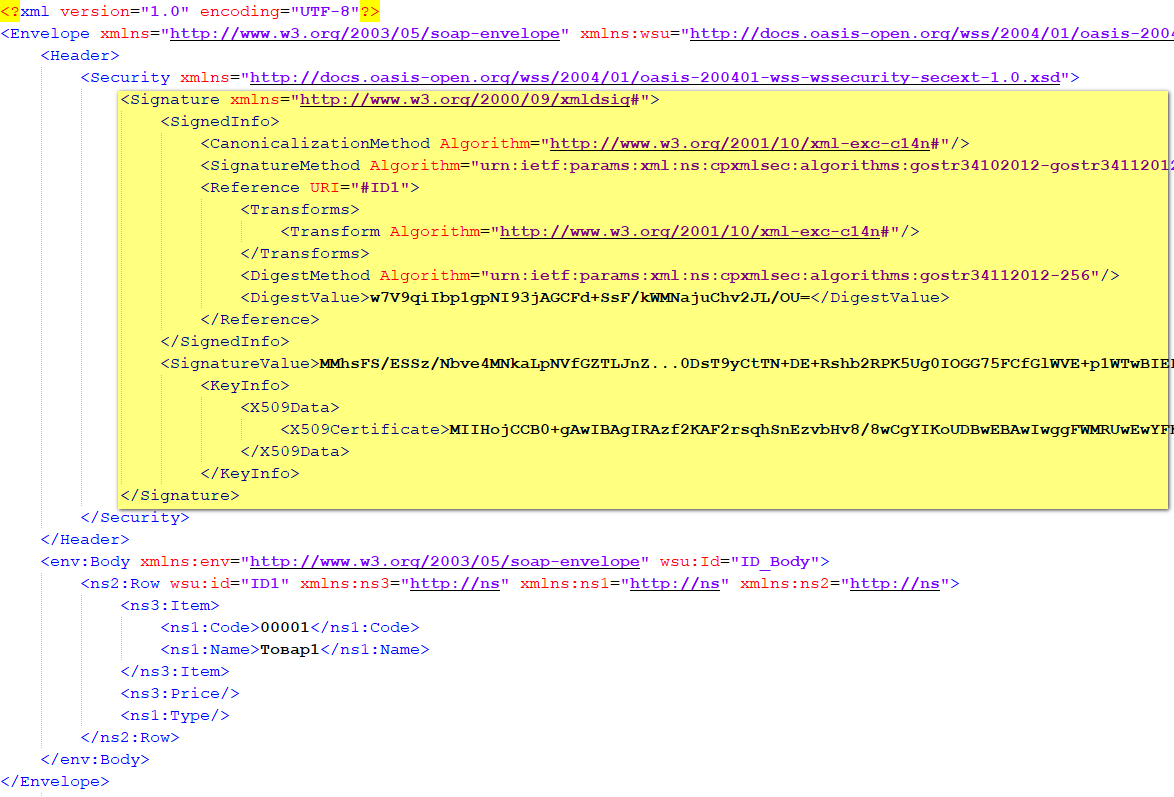
Но также они могут располагаться и в блоке Body.

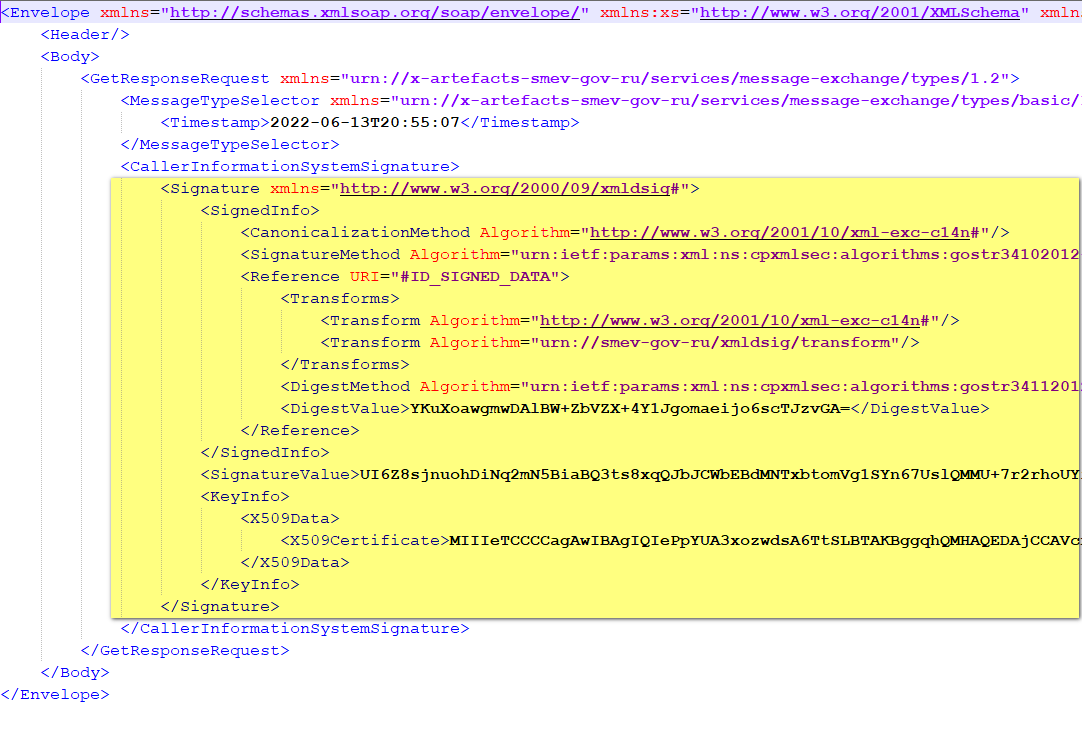
В одном XML документе может быть несколько электронных подписей, соответственно, несколько блоков XMLDsig.

Конкретные уточнения этих требований обычно указываются в документации к конкретной системе обмена информацией.

Стандарт описывает блок хранения электронной подписи и поля-теги, которые в нём должны быть расположены.

Основной, корневой блок должен называться Signature и принадлежать пространству имен «http://www.w3.org/2000/09/xmldsig#».

Вложенные блоки:

• SignatureValue — содержит значение подписи.
• KeyInfo — содержит значение сертификата подписи.
• SignedInfo — сведения о подписанных данных:
• CanonicalizationMethod — метод каноникализации (о том, что это такое ниже). Обычно содержит атрибут Algorithm с одним и тем же значением, как в примерах.
• SignatureMethod — указывает на алгоритм подписи (например, ГОСТ 2012).
• Reference — одна или несколько ссылок на исходные подписываемые данные.

Каждый элемент Reference (часто он один) — это ссылка на подписанный фрагмент XML. Для указания этой ссылки у исходных данных ставится атрибут Id, а в тег Reference указывается атрибут URI. В примере мы хотим подписать часть документа — блок Row. Для этого ему дали атрибут Id = «ID1» и сослались на этот Id в блоке Reference.

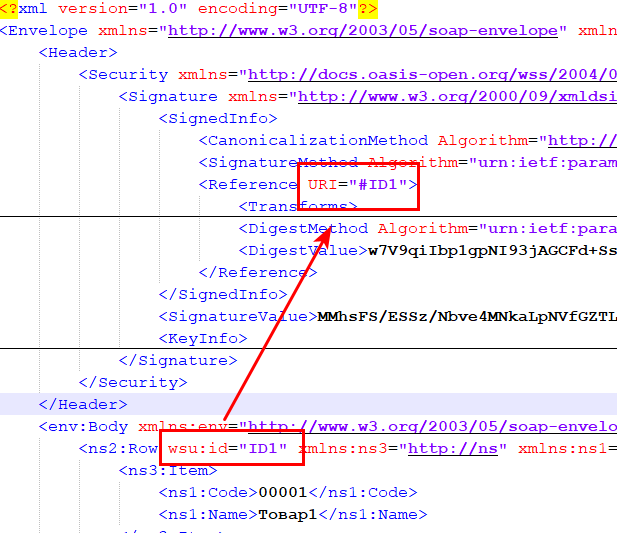
Также в блоке Reference присутствует три подраздела:

1. DigestMethod — указывает алгоритм хеширования.
2. DigestValue — указывает значение хеша подписанных данных (в примере — блока Row).
3. Transforms — содержит несколько вложенных элементов Transform, описывающих трансформации (о них тоже ниже).

Таким образом, чтобы подписать XML документ подписью XMLDSig надо дополнить документ сформированным блоком Signature и заполнить в нем несколько тегов-полей.

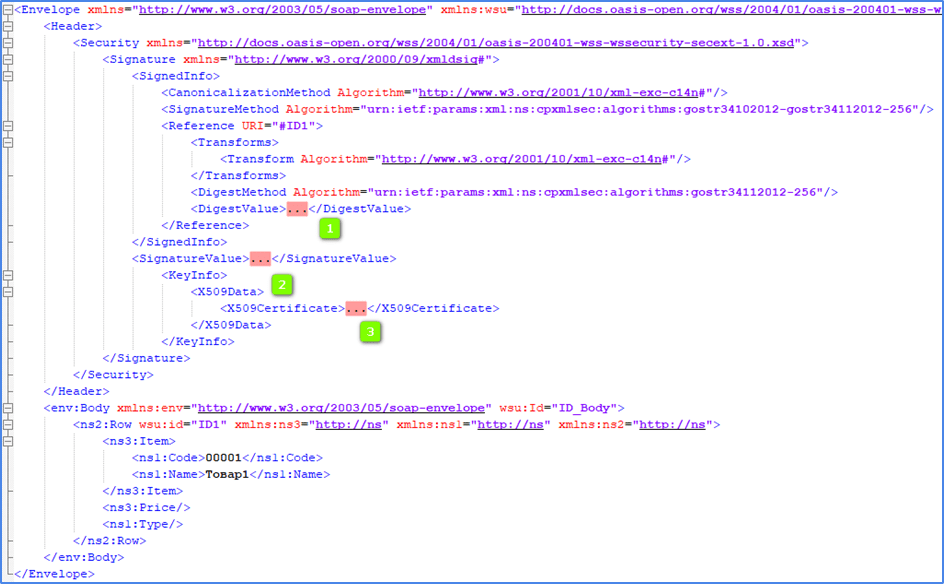
Обычно эти три отмеченных элемента:

1. В первое поле помещается дайджест, он же хеш подписанных данных.
2. Второе поле содержит значение подписи.
3. Третье поле — сертификат.

При этом поле подписи должно содержать значение «сырой» подписи, то есть свободное от разных форматов и оберток. Только те байты, которые возвращает криптографический алгоритм. Поэтому здесь нельзя использовать, например, подпись в формате CMS, которую мы уже умеем легко получать.

И здесь возникает проблема. Дело в том, что платформа 1С в лице менеджера криптографии не умеет вычислять «сырую» подпись. А также не умеет вычислять нужные хеш-функции.

Действительно, в платформе есть объект ХешированиеДанных, но с его помощью можно рассчитать хеш-суммы только самых распространенных алгоритмов:

А вот специфические, например, необходимый для подписи по ГОСТ хеш ГОСТ Р 34.11-2012 — рассчитать нельзя. С другой стороны, такой хеш может рассчитать криптопровайдер — это одна из его функций.

И здесь нам приходит на помощь внешняя компонента XMLDSig (ExtraCryptoAPI). В ней как раз есть недостающие функции:

• Вычисление «сырой» подписи.
• Хеширование при помощи криптопровайдера.
• И важный элемент — Каноникализация.

Что такое Каноникализация XML?

XML документы имеют следующую особенность: одни и те же, логически одинаковые, данные в XML можно представить разными способами, по-разному написав физическую структуру. И это проявляется следующим образом.

Предположим, отправитель решил составить XML документ, подписать электронной подписью и куда-то отправить. У него получился документ номер 1:

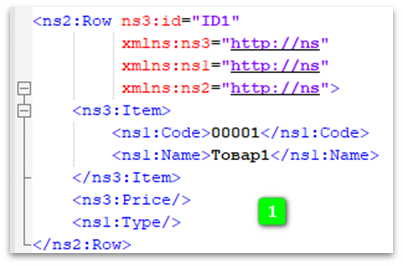
При передаче получателю этот документ пройдет через какие-то парсеры, библиотеки, возможно помещен внутрь SOAP пакета.

Может так получиться, что у получателя он уже будет выглядеть как фрагмент под номером 2. Возможно, какой-нибудь парсер решит документ немного облагородить.

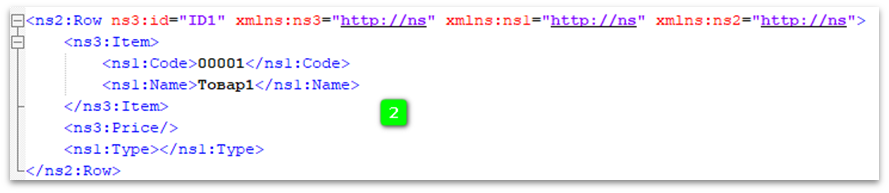
Это не ошибка, ведь логические данные одинаковы, содержат одинаковую информацию, просто отформатированы по-разному.

Тем не менее, при использовании криптографии это является проблемой.

Побайтовое представление этих документов различно. А, соответственно, будет разное значение хеша и несоответствие электронной подписи.

Для решения этой проблемы существует механизм «каноникализация» (Canonicalization, канонизация, C14N). Это определённый набор правил, описанный стандартом W3C, который применяется к документу с целью привести его в единый канонический вид.

Предполагается, что если у нас есть два документа XML, одинаковые логически, но при этом отличающиеся формой представления, каноническая форма у них будет одинакова и совпадать до байта.

Как изменится процесс передачи данных при использовании каноникализации:

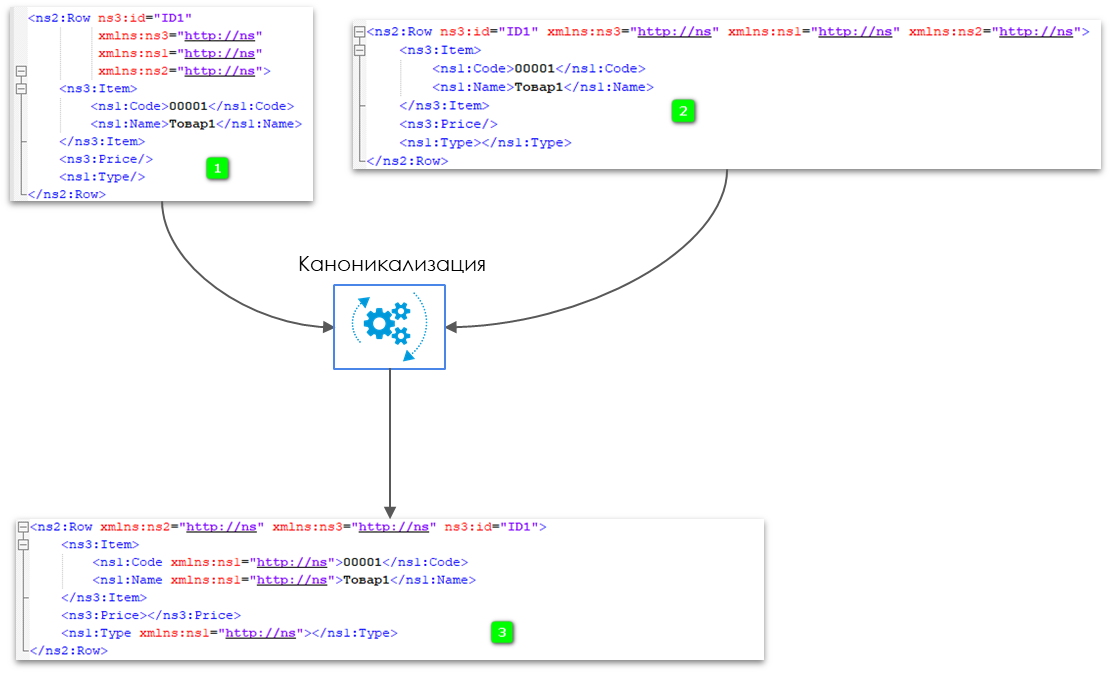
Отправитель, подготовив документ (1), сначала проводит его через процедуру каноникализации, получает каноническую форму (3) и над ней уже выполняет криптографические процедуры, например, получает хеш.

Далее отправляет по каналам связи каноническую или исходную форму документа.

Получатель, в свою очередь, загрузив документ (который, почему-то в процессе передачи преобразовался к форме (2)), также вычислит каноническую форму и опять получит такой же документ (3). Теперь над этим документом можно выполнять вычисления. Результат криптографических процедур, например, расчет хеша, теперь сойдется с результатом у отправителя.

Как раз использованный алгоритм каноникализации мы должны указать в разделе CanonicalizationMethod блока Signature, а также в разделе SignedInfo/Reference/Transforms/Transform.

Обычно и там и там указывается Algorithm="http://www.w3.org/2001/10/xml-exc-c14n#".

Дополнительные трансформации XML

Кроме того, стандарт XMLDsig позволяет выполнять не только каноникализацию типовым алгоритмом, но и вводить свои собственные так называемые трансформации.

На практике, мы сталкивались с такой особенностью в системе СМЭВ.

СМЭВ — система межведомственного электронного взаимодействия, государственная система для обмена данными между учреждениями.

В этой системе документ дополнительно к каноникализации XML надо преобразовывать специальным алгоритмом «трансформации СМЭВ». Таким образом, исходный документ XML проходит еще одну стадию прежде, чем получит каноническую форму (по версии системы СМЭВ):

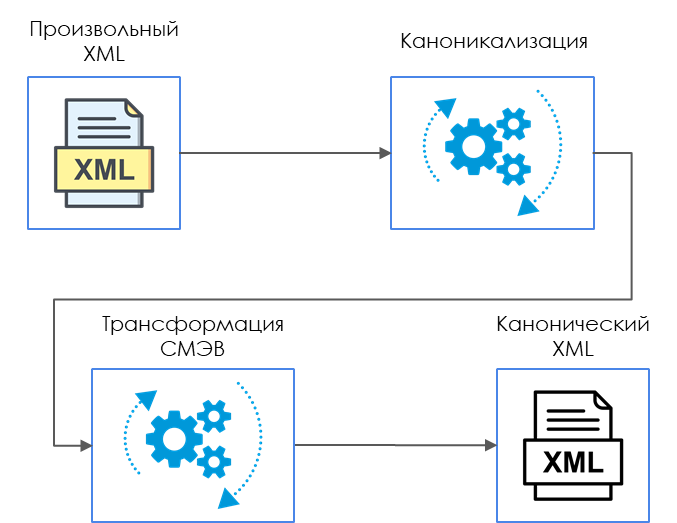
В последнее время взаимодействие с этой системой все более востребовано и в компоненте XMLDSig, а также в БСП появилась процедура для этого преобразования.

В случае использования дополнительной трансформации мы также должны указать это в блоке SignedInfo/Reference/Transforms/
Transform, еще одной строкой:

Создание подписи XMLDsig

Рассмотрим пошагово, как создать подпись XMLDSig. Связанный с преобразованиями XML код оставим за кадром.

Предположим, у нас есть исходный XML документ, например SOAP-пакет и мы хотим подписать его часть — блок «Row».

Начинаем с того, что подготавливаем структуру определённого формата для хранения подписей.

Здесь есть три фрагмента, которые надо заполнить. Что в них размещается мы уже рассмотрели ранее. Все значения записываются в виде Base64 строки.

Из исходного текста нужно выделить этот блок Row отдельно и получить его каноническую форму. Для этого мы пользуемся методом компоненты XMLDSig, который называется C14N(). Для указания, какой конкретно блок необходимо выделить и преобразовать каноническому виду, используем выражение XPath.

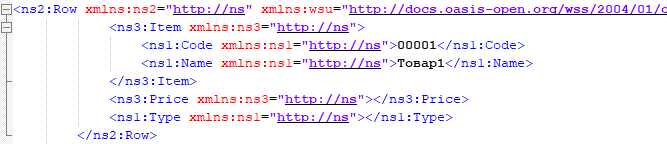
Здесь можно обратить внимание на табуляции — все табуляции сохранились. То есть несмотря на то, что мы блок выдернули из контекста XML, его каноническая форма по-прежнему содержит все пробельные символы, отступы между тегами. Теперь уже над этой канонической формой будем выполнять криптографические операции — вычислять хеш.

Вычисляем хэш этой строки. Это тоже делается при помощи компоненты. Каким конкретно алгоритмом мы рассчитываем хеш указывается при помощи так называемого OID — это специальный идентификатор, присвоенный тому или иному алгоритму. Например, здесь это ГОСТ Р 2012.

Получим вот такое значение:

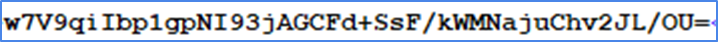
Ранее полученный из хранилища сертификат преобразуем в Base64.

И располагаем эти полученные значения в ранее подготовленной структуре в предназначенные для них места (1, 3).

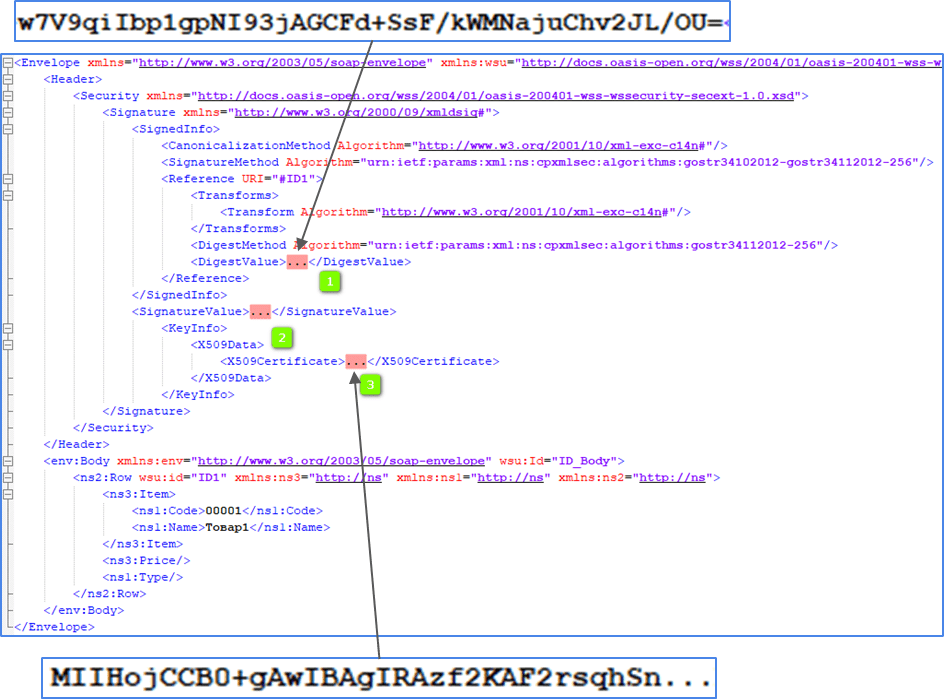
В DIgestValue (1) помещаем хеш, в X509Certificate (3) — сертификат.

Мы получили уже частично заполненную конструкцию.

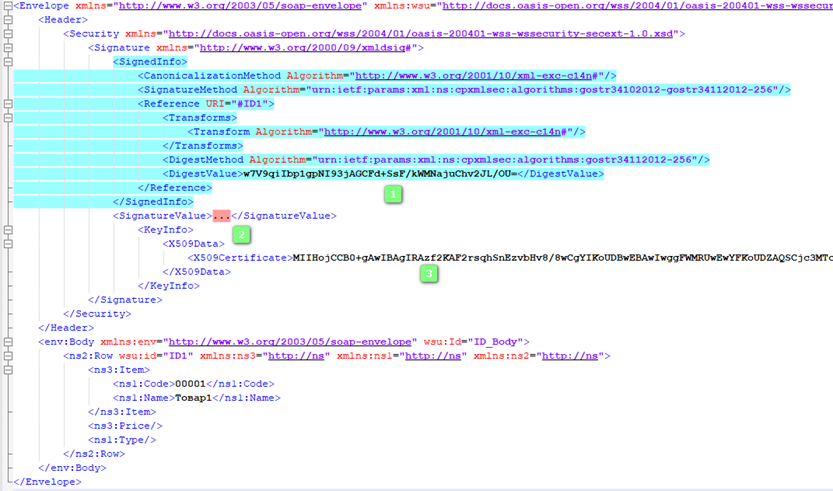
Следующий шаг, собственно, вычисление подписи. Но подписывать мы будем не блок Row (с которого все начиналось), а блок SignedInfo, в которой мы ранее поместили хеш (так устроен этот формат подписи).

В тексте этот блок выделен цветом. Здесь также надо применить процедуру каноникализации.

Электронную подпись необходимо получить именно «сырую» — непосредственно то значение, которое дает на выходе криптографическая функция. Для получения подписи используем функцию Sign() компоненты XMLDSig. Так же как мы сделали это с блоком Row, вызываем функцию каноникализации C14N(), а затем вызываем функцию Sign() и получаем «сырое» значение подписи в формате base64.

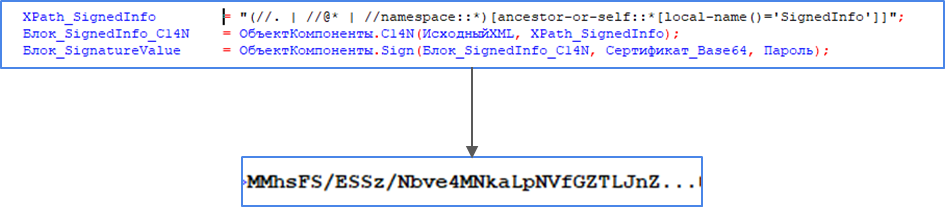
Полученное значение размещаем в соответствующее место структуры, помеченное здесь цифрой (2) — «SignatureValue»

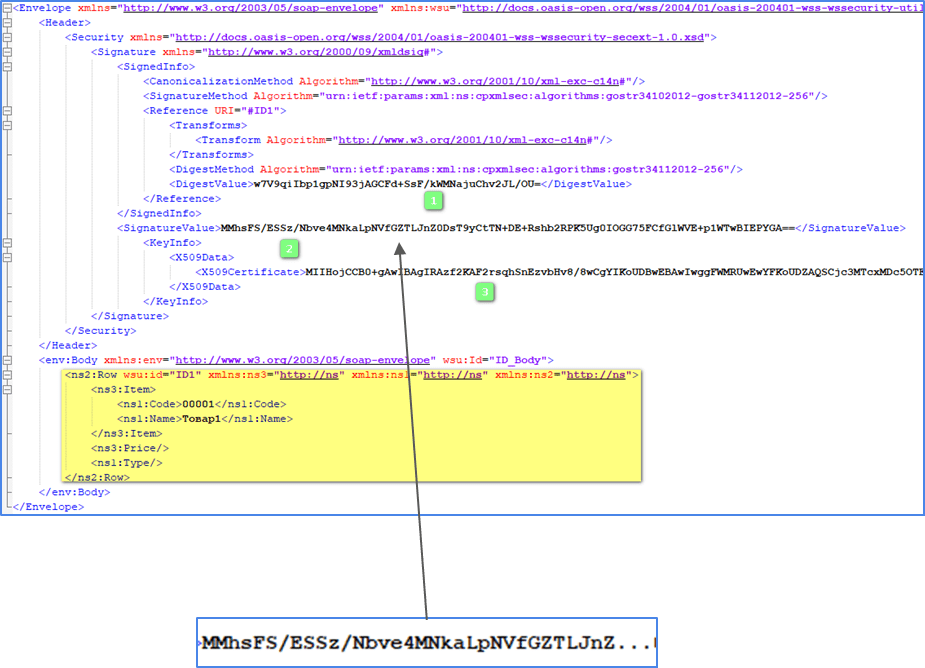
Теперь документ подписан. Его можно отправлять другому участнику взаимодействия или обмена.

Продолжение следует

Это первая статья цикла про криптографию и шифрование для 1С. В ней мы дали историю развития вопроса, начальные теоретические сведения о математическом аппарате шифрования, поговорили о терминологическом поле, которое весьма насыщенно. Привели практические примеры из жизни специалистов 1С, где понадобилось разобраться в форматах, а также поняли, что есть в платформе в этой части, а чего все же не хватает.

В следующей части мы разберем практические вопросы получения ключей, законодательство и настройку в программах 1С.