Оглавление
- Постановка задачи
- Что мы хотим получить?
- Откуда возникает беспорядок в справочниках
- Возможные способы решения задачи
- Математические подходы решения задачи
- Возможные подходы к решению задачи
- Пробьем стену лбом
- Модель «расстояние Левенштейна»
- Предобработка данных. Признаки — это наше все!
- Гистограммы сообщения
- Модель «Косинусная дистанция между векторами»
- Учет важности части слов механизмом самовнимания
- Нейросетевая «Метрическая модель»
- Модель «Наивный байесовский классификатор»
- Модель «Нечеткая логика»
- Промежуточный вывод
Данная статья представляет собой первую часть двусоставного цикла публикаций, посвященных решению задачи поиска дублей в справочниках. В первой части мы постараемся погрузить в теоретические основы задачи и дать ряд математических подходов для ее решения. Во второй части статьи, выход которой запланирован на декабрь 2023 года, мы предоставим практическую сторону вопроса, а также покажем интеграцию с 1С.
Постановка задачи
Любому без исключения проекту на 1С свойственно работать с такой сущностью, как справочник. Справочник — это постоянно пополняемый список. И если нет жесткого регулирования такого пополнения, например, через ИНН и КПП организаций, то возникает проблематика дублей. Один из «страдающих» в этом смысле справочников — это справочник Номенклатура. Однажды завели позицию «Картошка отварная», в другой же раз «Отварная картошка». Могут использоваться перестановки слов, их сокращения, при этом самые разнообразные. Таким образом список приходит в неустойчивое состояние, которое ведет к производным сложностям учета: пересортице, отрицательным остаткам, избыточной инвентаризации.
Совершенно очевидно, что с таким положением вещей мириться никак нельзя и необходимо решать задачу. Назовем её условно «дубли номенклатуры».
Оказывается, для решения задачи нам придется погрузиться достаточно глубоко в математический аппарат, классифицировать возможные коллизии дублей и удостовериться, что без погружения в математику всерьез задачу такого класса решить невозможно.
Что мы хотим получить?
- Разработать алгоритм, который будет давать подсказку пользователю, что вновь записываемая позиция является дублем уже существующих в справочнике.
- Алгоритм должен работать достаточно быстро (не более 2–3 секунд) при условии, что в справочнике 100 тысяч позиций.
- Алгоритм должен иметь возможность выдавать ранжирование по «похожести» строк.
- Алгоритм должен обучаться быстро. Желательно практически сразу же после ввода новой строки — записи в базу данных. Данное требование выполнимо не всегда.
Откуда возникает беспорядок в справочниках
Как всегда, основная проблема — это человек, и еще раз человек:
- Перестановка слов в наименовании.
- Избыточность в наименовании — желание поточнее описать учетную сущность.
- Усталость оператора, вследствии чего оператор начинает сокращать наименования.
- Копирование текста из другой учетной системы (например, Excel) — в результате копируются «невидимые символы», например, перенос строки внутри предложения.
- Особняком стоят числовые ошибки, когда, например, вместо 250 грамм пишут 0,25 кг.
- Орфографические ошибки или опечатки.
Возможные способы решения задачи
Административные методы
- Вводим единые классификаторы.
- Разрабатываем и внедряем инструкций по ведению номенклатурной базы. Пожалуй, это единственный работающий подход среди административных. Но его сложность в большой организации — это исполнение на всех этапах функционирования системы.
- Жестко — увольняем всех и будем сами вводить. Это, конечно, шутка :)
Инженерные методы
- Каждая позиция штрихкодируется и вводится через сканеры. Этот метод граничит с административным и не всегда исполним. Например, если речь идет о кухне с огромным количеством разнообразных ингредиентов.
- Применяем математические методы. Это и будет составлять содержание данной статьи.
Математические подходы решения задачи
Определим возможные виды коллизий и приведем примеры
- Опечатки:
- «Мнеральная вода».
- «Менеральная вода».
- Транслитерация:
- Coca-cola → Кока-Кола.
- Pepsi → Пепси.
- Borjomi → Боржоми.
- Сокращения в наименованиях:
- Мин. вода.
- Минер. вода.
- Перестановки слов:
- Вода минеральная.
- Минеральная вода.
- Использование чисел в наименованиях:
- Минеральная вода 1,5 литров.
- Минеральная вода 2 л.
- Использование сокращения единиц измерений:
- Литров, л., лит.
- Штук, шт., ш.
- Особняком стоит проблема перевод единиц измерения друг в друга:
- 0.5 л = 500 мл.
- 1000 кг = 1 тонна.
- Использование дополнительных символов (пробелы, табуляция, скобочки, звездочки и т.д.):
- Лист RV-100-dm 1000 × 2000 × 2 мм.
- Лист RV-200-kn 1000 × 2000 × 3 мм.
Примечание: использование единиц измерения, дополнительных символов может повлечь за собой отличие слов/предложений всего на эти особенности, что для человека не является проблемой, а для программы может быть достаточно сложным для разбора.
Возможные подходы к решению задачи
Пробьем стену лбом
Первый и самый наивный (не путать с наивным байес-ом — см. далее) способ — давайте просто разобьем тестируемую строку на слова и поищем такие же слова в других предложениях.
Преимущества:
- Думать над алгоритмом особенно не надо.
- На малых выборках работает быстро.
- Если оператор аккуратно придерживается правил, то работать будет хорошо.
Недостатки (вытекают из преимуществ):
- Много над алгоритмом не подумали — не учтем много нюансов. Например, простое сокращение слов ведет к неразрешимости задачи.
- Если выборка большая, то это очень долго.
- Даже малейшее изменение окончания слова и алгоритм будет ошибаться.
Стоит отметить, несмотря на то, что подавляющее большинство коллизий таким способом неразрешимо, подход продолжает пользоваться спросом.
Модель «расстояние Левенштейна»
Расстояние Левенштейна или редакционное расстояние — метрика, измеряющая расстояние между двумя последовательностями символов. Чем больше расстояние, тем более различны строки. Для двух одинаковых последовательностей расстояние равно нулю. Данное редакционное расстояние между двумя последовательностями символов определяется как минимальное количество одно символьных операций (удаления, вставки или замены), необходимых для превращения одной последовательности символов в другую.
Например, расстояние между словами «Австрия» и «Австралия» по Левенштейну составит 2 — понадобится два удаления:

Это классическая задача динамического программирования.
С точки зрения применения в поиске дублей, определение расстояния между словами или текстовыми полями по Левенштейну обладает следующими недостатками:
- При перестановке местами слов или частей слов, удаления символов из слова получаются сравнительно большие расстояния:
- «Минеральная вода 1л» и «минер вода 1л» — здесь расстояние Левенштейна равно 6 — очень большое, надо удалить 6 символов, чтобы получить вторую строку.
«Минеральная вода 1л» и «минеральная вода 2л» — здесь расстояние Левенштейна равно 1 — очень малое, нужно в первой строке 1 поменять на 2.
Но ясно, что «минер вода 1л» по смыслу более близко к «Минеральная вода 1л», чем «минеральная вода 2л» — т. к. литраж имеет очень большое значение.
- Расстояния между совершенно разными по смыслу короткими словами оказываются небольшими, в то время как расстояния между очень похожими по смыслу длинными словами могут оказаться значительными:
- Слон и сон — расстояние равно 1, нужно просто удалить в слове слон букву л, но по смыслу это совершенно разные слова.
Таким образом красивая математика из области спортивного программирования совершенно непригодна для полноценного решения задачи в практической плоскости.
Предобработка данных. Признаки — это наше все!
Что такое это модное слово «признаки»? Давайте разберемся.
Представим, что перед нами сидят кот и птица. Как бы мы объяснили другому человеку, который не видит этих двух животных — кто из них кто?
Наверное, так: «Первое животное мурлыкает, у него есть усы, а у второго есть крылья».
Вот они — признаки. Не важно, какого цвета кошка, какой она породы — другой человек сразу поймет, что это кошка. Также и с определением птицы — крылья есть только у птиц.
Т. е. признаки — это некоторые свойства класса-объекта, его характерные черты, уникально его выделяющие среди других классов-объектов.
Давайте выделим эти «признаки» для наших строк.
Но прежде чем их выделить необходимо избавиться от шума и произвести в известном смысле нормализацию.
Допустим, введена строка «Минеральная вода»:
- Произведем удаление всех «неполноценных» слов, то есть предлогов, союзов, междометий «на, в, из, с» и т. д. Таким образом строка «Минеральная вода разлитая в бутылки» будет преобразована в «Минеральная вода разлитая бутылки».
- Удалим точки, запятые, двоеточия, спецсимволы (*, (, ), ..) и пр. Приведем существительные к форме «бутылки» → «бутылка». Также приведем все слова к нижнему регистру.
- Произведем обратную транслитерацию слов (Pepsi → Пепси).
А теперь собственно к извлечению признаков.
Есть такие красивые слова — биплет, триплет. Они и будут для нас основой для построения признаковой части слов.
Что это?
Би — два, три — ну это три :)
Т. е. биплет — это просто разбиение слова на последовательности по две буквы с шагом смещения в один символ.
А триплет — на три буквы.
Вот пример — возьмем слово слон:
- биплеты — сл, ло, он;
- триплеты — сло, лон.
Введем пару необходимых определений для успешности дальнейшего изложения.
Информационная энтропия — это мера непредсказуемости появления какого-либо символа первичного алфавита.
Первичный алфавит — это набор букв, биплетов, которыми мы можем оперировать. Например, если мы работаем только с целыми числами, то наш первичный алфавит — это числа от 0 до 9, т.к. любое целое число можно представить из набора цифр от нуля до 9. Если мы рассматриваем русский язык, как средство коммуникации, то наш первичный алфавит — это буквы кириллицы.
Чем реже появляется в словах какой-либо символ из первичного алфавита, тем сильнее будет уменьшаться информационная энтропия при его появлении в исследуемом слове.
Например — если у нас есть слова:
- принтер,
- интернат,
- интерно.
Если нам скажут биплет ин (или ер) — то он слабо идентифицирует слово, т. к. эти биплеты есть во всех трех словах. А вот появление биплета но однозначно идентифицирует слово интерно, т. к. этот биплет есть только в этом слове. Поэтому информационная неопределенность становится равной нулю, при появлении биплета но и не изменяется при появлении биплета ин (т. к. этот биплет входит во все три слова).
Энтропию возможно посчитать. Давайте посмотрим на то, как это сделать.
Энтропия сообщения (формула Шеннона)
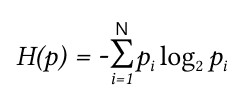
Или:
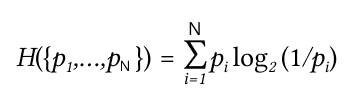
H(x) — это средняя энтропия сообщения.
p — вероятность появления биплета в сообщении.
N — количество случайных событий (биплетов в нашем случае).
Формула Лапласа для равновероятных событий
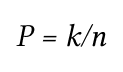
Вероятность (P)— количество положительных исходов (k), деленное на общее число равновероятных возможных исходов (n).
Пример расчёта информационной энтропии
Представим, что у нас есть монета, где обе стороны орел.
Тогда вероятность выпадения орла составляет 2/2 = 1, т. е. орел выпадет всегда. А вот выпадение решки будет 0/2 = 0, т. е. выпадения решки невозможное событие.
Если у нас «правильная» монета, где есть сторона орел и есть сторона решка, то выпадение орла будет ½ = 0.5, и выпадение решки будет ½ = 0.5.
Информационная энтропия будет
– (½ log21/2 + ½ log21/2) = – (–½ – ½ ) = 1
Если у нас есть «неправильная монета», где вероятность выпадения орла меньше чем вероятность выпадения решки — допустим, вероятность выпадения орла 0,1, а вероятность выпадения решки 0,9 (этого можно добиться если на стороны решки припаять грузик — это будет эффект бутерброда), то информационная энтропия будет следующая
– (0.1 log20.1 + 0.9 log20.9) = – (–0,3322 – 0,1368) = 0,469
Т. е. для равновероятных событий информационная энтропия больше, чем для неравновероятных. Это и понятно, т. к. получение маловероятного события сильнее уменьшает энтропию, чем получение равновероятного события (встреча крокодила при прогулке в Москве более интересное событие, чем встреча голубя или воробья):
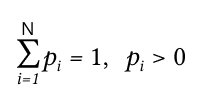
Энтропия Шеннона оценивает среднее количество информации (математическое ожидание), которое содержится в значениях случайной величины.
Примечание:
Для равновероятных событий формула Шеннона упрощается до формулы Хартли:
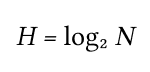
где N — размер словаря, элементы которого равновероятны
Таким образом, энтропия системы является суммой с противоположным знаком всех относительных частот появления биплета с номером i, умноженных на их же двоичные логарифмы
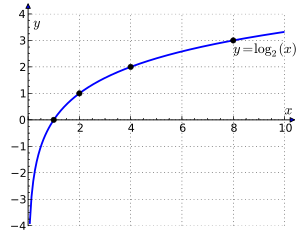
рис. Функция логарифма
Информация в сообщении — это разница неопределенностей до получения сообщения и после:
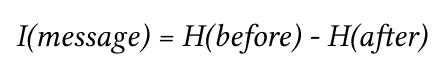
Измеряется в битах.
Например, Ваня загадал число от 0 до 100.
Неопределенность составляет log2100 = 6,644 (у нас все числа равновероятны).
Мы спрашиваем — это число <= 50?
Нам сказали, что да.
Тогда неопределенность после этого сообщения будет log250, или один бит информации. Т. е. энтропия (мера неизвестности) «что это за число» снизилась, т. к. мы только что узнали, что это точно не 70, и не 90. А меньше либо равно 50.
Так задавая вопросы (бинарные по своей сути — Да/Нет) мы получаем уменьшение энтропии, пока точно не узнаем, что это за число. Например, что это число 13 и энтропия не станет 0, т. к. энтропия сообщения, которое известно, равна 0 (мера неопределенности нулевая).
Частоты биплетов имеют интервал от >0 до 1.
Из графика логарифма видно, что чем больше частота появления биплета, тем большее значение логарифма.
В пределе, при частоте равной 1, значение логарифма равно 0, т. е. вклад в сумму H(x) от биплета с большой частотой тем более мал, чем частота появления биплета больше. И наоборот, чем меньше частота появления биплета, тем больше вклад логарифма в H(x), а следовательно и энтропия сообщения будет больше.
Когда мы разобрались с формулой, то становится понятным, как нам действовать.
Разбиваем слова на биплеты, а не просто на буквы, т. к. биплеты несут в себе больше информации о составе предложения. Это следует из того, что при разгадывании слова, если назвать две буквы, то легче слово отгадать, чем если назвать одну букву. Информационная энтропия при открывании 2-х букв уменьшается больше, чем при открывании 1-ой буквы.
Также, например, появление биплета «ан» уменьшает информационную энтропию больше, чем буквы а н по отдельности.
Конечно, разбиение на триплеты потенциально информативней, чем на биплеты, но не стоит забывать, что наш конечный первичный алфавит будет состоять из комбинаций по три буквы, что очень велико.
Почему триплеты более информативны, чем биплеты и почему мы все таки в нашей задаче отдаем предпочтение биплетам?
Большая информативность триплетов следует из простого логического рассуждения — чем больше букв мы можем узнать о неизвестном слове, тем нам легче его разгадать. Допустим, мы загадали слово «Доклад». Если мы сообщим одному человеку, который должен отгадать это слово биплет «До», а другому триплет «Док», то у второго шансов будет больше.
Однако специфика нашей задачи такова, что мы имеем дело с короткими текстами и словами. Наименование, как правило, колеблется в пределах от 10 до 50 символов и в случае триплетного разбиения инвариантность, то есть неизменяемость, уменьшается, признаков становится меньше.
Исходя из этих простых логических рассуждений можно сделать вывод, что разбиение на биплеты будет достаточным для создания полного векторного представления коротких предложений.
Отдельно стоит рассмотреть вопрос, почему мы выбрали построение биплетов со смещением в один символ, а не в два. Т. е. если есть слово «погода», то для биплетного представления со смещением в один символ будет:
ог
го
од
да
При смещении на два символа:
го
да
Ответ на этот вопрос также попробуем вывести из логических рассуждений.
У нас достаточно короткие предложения и размер словаря при смещении по две буквы будет меньше, что уменьшает размерность словаря и это, конечно, хорошо скажется на обобщающей способности алгоритма. Но если мы проанализируем состав предложений, то можно увидеть — в предложениях, с которыми мы работаем часто встречаются числовые значения: Вода минеральная 1 литр, Минеральная вода 2 литра.
Допустим у нас есть наименование «вода 245».
При разбиении со смещением в 1 символ будет:
од
да
а2
24
45
При разбиении со смещением в 2 символа будет:
да
24
Т. е. последний числовой параметр (5) будет выкинут, что является недопустимым в данном контексте решения задачи.
Но если предложения имеют большую длину или нам не так важны числовые параметры, то возможно использование и разбиения по два символа.
Итак, разбиваем строку «Минеральная вода» на биплеты по две буквы со смещением в одну букву:
ин
не
ер
ра
ал
на
ая
во
од
да
Но как нам закодировать весь этот набор биплетов? В этом нам поможет гистограмма сообщения.
Гистограммы сообщения
Гистогра́мма — графическое представление данных, содержащее сколько и каких событий случилось за определенный период времени (определение применительно к статистике).
Примечание: приведенная гистограмма — это просто пример вида гистограммы, а не гистограмма, рассчитанная по нашим данным.
В нашей задаче по горизонтали откладывается номер биплета, а по вертикали количество таких биплетов в предложении/слове.
Нужно составить словарь гистограммы. Для этого можно составить все возможные комбинации биплетов русского языка — это будет 31 буква, мы не станем учитывать экзотические буквы «Ъ», «Ь». Строго говоря, необходимо учесть числа от 0 до 9, но для простоты изложения теоретической части не станем этого делать.
Всего получится 31 × 31 комбинаций — 961.
Это много. Можно попробовать уменьшить. Можно сделать так: используя словарь найдем по тексту частоты появления каждого биплета. Если частота очень большая, то этот биплет будем относить к групповому биплету, т.е. биплету, который очень часто встречается в тексте. Частоты посчитаем так — количество появления биплета во всем тексте деленное на общее количество биплетов в тексте.
Обоснование: появление в предложении биплета, частота появления которого очень высока, приводит к малому уменьшению информационной энтропии сообщения.
Следовательно, мы можем попробовать сгруппировать биплеты с большой частотой появления в один общий сводный биплет и на гистограмме такие биплеты будут «занимать» ровно одну позицию по координате X.
В итоге у нас получится N биплетов — это и назовем словарем, т. е. с помощью этого словаря мы сможем закодировать любое слово или предложение.
Далее имея предложение, мы можем посчитать количество биплетов в нем. В массиве длиной N, где каждая позиция соответствует отдельному биплету из словаря, проставим количество биплетов в предложении на позициях биплетов в гистограмме. В итоге мы получим гистограмму предложения. Эта гистограмма не зависит от порядка слов и биплетов в предложении, а зависит только от конечного набора биплетов в предложении. Это так называемый инвариант:
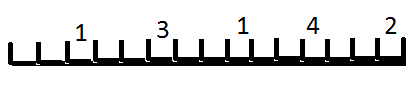
На рисунке числа — это количество появления биплетов в проверяемом предложении.
Примечание:
Если бы у нас появление каждого биплета было равновероятным событием, то фактически, мы имели бы битовое слово длиной 961 бит, в котором каждая позиция в битовом слове содержит 1 или 0, то по формуле Хартли получаем:
log2 и это очень большое число :)
Например, вот битовые слова длины 5:
00000, 00001, 00010, 00011, 00100, 00101, ... , 11100, 11101, 111110, 11111
Их 32 штуки (11111 = 31 и еще + 1 от 00000). log2(32) = 5, т. е. неопределенность битового слова длины 5 равна 5.
Именно столько неизвестных бит в неизвестном битовом слове длины 5.
Таким образом, каждый знак в битовом слове называется битом, но ещё бит — это единица измерения неопределенности. И из этого примера понятно почему.
Но т. к. появление биплета у нас на позиции n не равновероятное событие, то нужно применять не формулу Хартли, а формулу Шеннона.
Из-за того, что длина гистограммы очень большая, а заполнение ячеек биплетов редкое — это разреженные данные, что накладывает отпечаток на использование алгоритмов. Т. е. алгоритм должен быть нечувствителен к такому виду представления данных.
Введем коэффициент разреженности матрицы K:
K = N0/S
N0 — количество ненулевых элементов в матрице, в нашем случае в гистограмме.
S — всего элементов в матрице, в нашем случае в гистограмме.
Если K < 0,5, то можно говорить, что матрица разреженная.
В нашем случае, K < 0,5, т. к. предложения, как мы договорились ранее, короткие. Поэтому количество биплетов мало по сравнению с «длиной» гистограммы.
Примечание:
- Перетасовка слов в предложении не будет иметь значения, т.к. гистограммы будут идентичны. Это следует из самой природы наших признаков (биплетов).
- Конечно, могут быть случаи, когда предложения разные, и при этом гистограммы одинаковые. Но это крайне и крайне редкое событие. Особенно для достаточно длинных предложений.
Итак, мы теперь умеем представлять каждое предложение в виде биплетов, сгруппированных в гистограммы.
Причем длина гистограммы не зависит от длины предложения.
Как мы можем теперь сравнивать эти гистограммы? Это ведь не слова чтобы просто сравнить побуквенно...
И тут нам поможет царица всех наук — математика!
Модель «Косинусная дистанция между векторами»
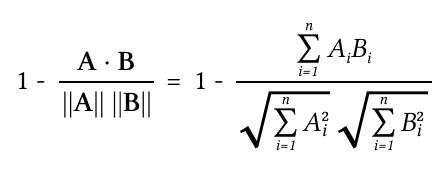
Где A и B векторы слов, а ||A|| и ||B|| их длина, n — количество элементов массива соответствующих вектору.
Косинусное подобие (cosine similarity) — метрика, используемая для определения сходства между двумя векторами. Она вычисляется как косинус угла между двумя векторами и может принимать значения от −1 до 1. Значение 1 означает полное сходство, а значение −1 — полное несходство.
Косинусная дистанция (расстояние) (cosine distance) — это когда из единицы вычитаем косинусное подобие. Тут наоборот — чем меньше, тем лучше.
Например, вектор слова «вода» будет ближе к слову «огонь», чем к слову «земля», поскольку косинусная дистанция в первом случае меньше.
Поясним это на примере.
Произведем расчет вектора слов вода, озеро, огонь.
Для этого составим словарь — у нас есть буквы в, о, д, а, з, e, м, л, я, г, н, ь.
Сопоставим позиции для каждой буквы:
| Буква | Позиция |
|---|---|
| в | 0 |
| о | 1 |
| д | 2 |
| а | 3 |
| з | 4 |
| е | 5 |
| м | 6 |
| л | 7 |
| я | 8 |
| г | 9 |
| н | 10 |
| ь | 11 |
Т. е. длина нашего вектора будет равна 12.
Теперь на место каждой буквы каждого слова ставим 1 там, где есть буква входящая в слово:
Вода
| В | О | Д | А | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Итоговый вектор 111100000000
Земля
| З | Е | М | Л | Я | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Итоговый вектор 000011111000
Огонь
| О | Г | Н | Ь | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Итоговый вектор 010000000111
Примечание: здесь мы применяем самый простой режим кодирования без использования частоты появления букв и биплетного разбиения. Исключительно для демонстрации векторизации и сравнения расстояния между ними.
Произведем расчет косинусной дистанции.
Для векторов «Вода» (111100000000) и «Земля» (000011111000), учитываем, что квадрат 0 равен 0 и квадрат 1 равен 1:
Числитель (поэлементное умножение):
1 × 0 + 1 × 0 + 1 × 0 + 1 × 0 + 0 × 1 + 0 × 1 + 0 × 1 + 0 × 1 + 0 × 1 + 0 × 0 + 0 × 0 + 0 × 0 = 0
Знаменатель:
1 + 1 + 1 + 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 4
Взяв корень из четырех получим 2.
0 + 0 + 0 + 0 + 1 + 1 + 1 + 1 + 1 + 0 + 0 + 0 = 5
Взяв корень из пяти получим 2,23 (примерно).
Косинусная дистанция = 1 — 0 / (2 × 2,23) = 1 — 0 / 4.46 = 1 — 0 = 1
Для векторов «Вода» (111100000000) и «Огонь» (010000000111):
Числитель (поэлементное умножение):
1 × 0 + 1 × 1 + 1 × 0 + 1 × 0 + 0 × 0 + 0 × 0 + 0 × 0 + 0 × 0 + 0 × 0 + 0 × 1 + 0 × 1 + 0 × 1 = 1
Знаменатель:
1 + 1 + 1 + 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 4
Взяв корень из четырех получим 2
0 + 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 + 1 + 1 = 4
Взяв корень из четырех получим = 2
Косинусная дистанция = 1 — 1 / (2 × 2) = 1 — 1/4 = 1 — 0.25 = 0,75
| Вода | |
|---|---|
| Земля | 1.0 расстояние слова «Вода» до слова «Земля» |
| Огонь | 0.75 расстояние слова «Вода» до слова «Огонь» |
Т. к. мы используем косинусную дистанцию, то чем меньше значение, тем более похожи слова. Слово «Вода» ближе к «Огонь», чем к слову «Земля».
Это то же евклидово расстояние, но в отличие от него косинусное расстояние показывает, на какой угол нужно повернуть первый вектор, чтобы он стал коллинеарным второму или иначе говоря, чтобы два вектора лежали на одной прямой.
Т.к. у нас гистограмма, то перестановка слов не будет влиять на расчет косинусного расстояния между векторами (гистограмма инвариантна к этому преобразованию).
Следовательно, алгоритм такой — нужна уже рассчитанная гистограмма для всех предложений справочника «Номенклатура». Далее делаем расчет гистограммы для проверочного предложения и производим расчет косинусного расстояния со всеми предложениями справочника «Номенклатура». Выбираем наиболее малое значение. Это и будет наиболее похожее предложение из справочника «Номенклатура». Даже со списком справочника «Номенклатура» > 100000, расчет производится за приемлемое время (2–3 сек на CPU, на GPU — в разы быстрее).
Преимущества:
- Простая, и понятная математика.
- На вопрос «Почему это предложение более похоже на это предложение, а не на то?» ответ очень просто интерпретировать.
- Можно составлять списки, отсортированные по коэффициенту уверенности выданному алгоритмом, для каждого предложения по похожести на наше проверочное предложение.
- С ростом базы справочника время поиска растет линейно.
- Хорошо распараллеливается.
- Возможно применять некоторые приемы для ускорения поиска.
Недостатки:
- Нужно хранить в базе рассчитанные гистограммы для каждого предложения, что при достаточной большой длине словаря может быть накладно.
- Негибкость. Если мы хотим учесть части слов предложения как более весомые (об этом далее), то придется придумывать какие-то новые приемы.
Пример работы по модели косинусной дистанции
Сделаем допущение: алгоритм будет отбирать только те предложения из базы справочника «Номенклатура», косинусная дистанция которых с тестируемым предложением меньше или равно 0,3. Хорошие результаты получаются, когда этот параметр от 0,1 до 0,3 — чем меньше данный параметр, тем пессимистичнее результаты, т. е. чем меньше, тем более осторожно работает алгоритм. 0,3 в данном случае — это подбираемый гипер параметр, т. е. параметр, который мы подбираем для улучшения работы нашего алгоритма для данного метода.
| Тестируемое сообщение | Варианты выданные алгоритмом | Косинусная дистанция |
|---|---|---|
| Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм | 0 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.02 | |
| Для витрин светильничек — Shop CR190 3000K 24 V 18.4 900 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.07 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.09 | |
| Светильничик для витрин Shop CR190 3000K 24 V 18.4 900 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.02 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.04 | |
| Светильничик витрин Shop CR190 3000K 24 V 18.4 900 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.02 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.04 | |
| Светильничик витринный Shop CR190 3000K 24 V 18.4 900 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.07 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.09 | |
| Светильничик витринный //Shop// CR190 3000K 24 V 18.4 900 | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.08 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.01 | |
| Светил. витринный //Shop// CR190 3000K 24 V 18.4 900 | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.15 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.17 | |
| Светил. витр. //Shop// CR190 3000K 24 V 18.4 900 | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.14 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.17 | |
| Светил. витр. //Shop// CR190 24 V 18.4 900 | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.24 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.28 | |
| Светил. витр. //Shop// 24 V 18 4 900 | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм | 0.29 |
| Светил. витр. //Shop// 24 18 4 900 | not found in database |
Время работы алгоритма на базе данных из 15000 строк 0.8 сек
В таблице есть проблематичные строки
| Тестируемое сообщение | Варианты выданные алгоритмом | Косинусная дистанция для числовых векторов |
|---|---|---|
| Для витрин светильничек — Shop CR190 3000K 24 V 18.4 500 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.09 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.09 | |
| Для витрин светильничек — Shop CR190 3000K 24 V 20.4 500 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм’ | 0.12 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.12 |
Если мы меняем в тестируемом сообщение числовые параметры (в допустимых пределах, конечно), то модель реагирует на это так же, как и при смене букв (слабо), но это не совсем корректное поведение, потому что числовые параметры несут в себе важную информацию о предмете: рабочее напряжение, вес, размер и т. д. По существу, при смене числовых параметров модель должна учитывать это более весомо.
Учет важности части слов механизмом разных весов
Нам необходимо улучшить сравнение с учетом цифровых символов в наименованиях.
Идея состоит в том, чтобы вектор признаков, в котором биплеты буквенные и числовые вместе, разделить на два вектора — буквенные биплеты и числовые биплеты. Теперь будем рассчитывать две косинусные дистанции. Учет косинусной дистанции числового вектора (он в себе содержит только числовые биплеты) будем брать с повышенным коэффициентом.
Можно сделать просто — косинусную дистанцию для символьных векторов сравниваем с 0,3 (например), а косинусную дистанцию числовых векторов сравниваем так: (значение косинусной дистанции числовых векторов + (0,3) / 2) <= 0,3 — тогда отсечка по числовым векторам будет строже, чем по символьным.
Результаты
| Тестируемое сообщение | Варианты выданные алгоритмом | Косинусная дистанция для символьных векторов |
Косинусная дистанция для числовых векторов |
|---|---|---|---|
| Для витрин светильничек — Shop CR190 3000K 24 V 18.4 500 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм | 0.12 | 0.20 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.12 | 0.21 | |
| Для витрин светильничек — Shop CR190 3000K 24 V 20.4 500 мм | Светильник для витрин Shop CR190 3000K 24 V 18.4 900 мм | 0.12 | 0.26 |
| Светильник для витрин Shop CR190 3000K 24 V 18.4 600 мм | 0.12 | 0.27 |
Введение разного контроля позволяет отсекать по косинусной дистанции числового вектора. Добавочный параметр (у нас 0,3 / 2) — это подбираемый параметр: чем меньше, тем менее строго будет модель отсеивать похожие предложения.
Например, если добавочный параметр установим как 0,3 / 1,2, то:
| Тестируемое сообщение | Варианты выданные алгоритмом | Косинусная дистанция для символьных векторов |
Косинусная дистанция для числовых векторов |
|---|---|---|---|
| Для витрин светильничек — Shop CR190 3000K 24 V 18.4 500 мм | not found in database | ||
| Для витрин светильничек — Shop CR190 3000K 24 V 20.4 500 мм | not found in database |
Время работы алгоритма по двойным векторам больше — на 15000 строках справочника «Номенклатура» 3–4 сек, но можно снизить это время оптимизировав алгоритм.
Еще примеры без использования двойных векторов:
| Тестируемое сообщение | Варианты выданные алгоритмом | Косинусная дистанция |
|---|---|---|
| Вино Красное Сухое Шато Мон-Редон Лирак АОС 2014 14,5% 0,75л | Вино Красное Сухое Шато Мон-Редон Лирак АОС 2014 14,5% 0,75л | 0 |
| Вино Красное Сухое Шато Бомон о-Медок 0,75л | 0.26 | |
| Вино Шато Ла Гравьер Бордо АОС 2014 0,75л красное сухое 12,5% | 0.27 | |
| Вино Красное Сухое Шато Люсьер Бордо АОС 2014 12,5% 0,75л | 0.28 | |
| Вино Красное Сухое Шато Ла Тесоньер Медок АОС 2015 0,75л | 0.28 | |
| Вино Красное Сухое Шато Ла Тесоньер Медок АОС 2015 0,75л | 0.28 | |
| Вино Красное Сухое Шато Сегелонг Медок АОС 12,5% 0,75л | 0.29 | |
| Вино Красное Сухое Шато Ситран О-Медок АОС 0,75л | 0.29 | |
| Вино Красное Сух. Шато Мон/Редон Лир. 2014 14,5% 0,75лл | Вино Красное Сухое Шато Мон-Редон Лирак АОС 2014 14,5% 0,75л | 0.07 |
| Вино Красное Сухое Шато Бомон о-Медок 0,75л | 0.27 |
Примечание: можно сделать и проще — при получении данных просто сравнивать числовые характеристики в тестируемом сообщении, и в полученных похожих на него сообщениях. Их не будет много и алгоритм сравнения быстро справится с этой задачей.
Учет важности части слов механизмом самовнимания
Одна из проблем, возникающая при построении эмбеддингов (эмбеддинг — это фактически преобразование в нашем случае текста в некоторое другое представление, более удобное для работы) слов, — это неоднозначность естественного языка. При обучении на корпусе текстов, вектор эмбединга каждого слова получает фиксированные компоненты, которые не зависят от того смысла, в котором это слово встретилось в тексте.
Механизм внимания (точнее в этом случае самовнимания) модифицирует вектор эмбединга каждого слова, «подмешивая» к нему векторы его окружения (контекста) с некоторыми весами.
Допустим, есть предложение: «Я вчера стрелял из лука».
В этом предложении 5 слов.
Вычислим эмбеддинг каждого слова и обозначим их через vi (i от 0 до 4).
Учтем контекст слова «лук» v4 — вычислим его скалярные произведения с другими словами.
Полученные веса нормируем при помощи функции softmax, так чтобы их сумма равнялась единице, а значения лежали в диапазоне [0...1]:
Примечание: результат softmax-преобразования интерпретируем как вероятность. В данном случае нас не интересует вероятность собственно как вероятность — мы применяем такой прием для сопоставимости чисел, производим по сути операцию нормализации чисел.
Чем ближе к единице веса w′i, тем сильнее слово v4 похоже на слово vi. Построим теперь новый эмбеддинг слова «лук» в виде взвешенной суммы:
В результате вектор слова «лук» будет учитывать свое окружение — и в контекстном окружении будет лучшее «понимание», что в данном случае «стрелял» из оружия «лук». В предложении «я вчера ел салат из лука» — здесь контекстное окружение будет лучше учитывать, что в данном случае «лук» — чаще применяется к слову «салат».
Таким образом модель научится не только комбинации слов в предложении, но и будет «понимать» (в некотором смысле) контекст предложения, что очень важно для построения качественной модели.
Нейросетевая «Метрическая модель»
Нейро́нная сеть (также искусственная нейронная сеть, ИНС, или просто нейро́сеть) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети У. Маккалока и У. Питтса. После разработки алгоритмов обучения получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.
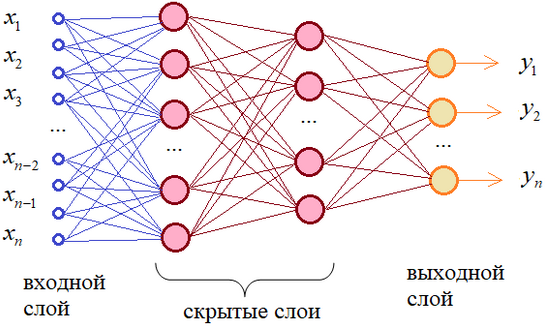
На вход нейросети подаем гистограммы сформированные из предложений нашей базы данных.
Сложность такого подхода состоит в том, что фактически, каждое наименование, на котором обучаем нашу нейросеть и есть класс, который мы и будем предсказывать. И тут встает задача — классов много, а представителей каждого класса очень мало — часто просто одно наименование. Просто взять и обучить обычный классификатор не получится — модель просто переучиться из-за малого количества представителей одного класса. Да и классов слишком много.
Как будем решать? Вспомним, как сейчас решается вопрос распознавания лиц — в этой задаче также мы имеем штучное количество (часто одно) фотографий лица человека, а людей может быть сотни тысяч, если не сотни миллионов. И также получается классов много, а представителей каждого класса — мало. И тут нам приходит на выручку метрическая модель.
Метрическая модель — вот наше спасение!
А давайте поймем, что такое наша гистограмма предложения?
Это ведь фактически переход от побуквенного предложения в пространство других признаков (гистограммное биплетное представление). Т. е. наша гистограмма описывает наше предложение, плюс к тому еще является сущностью, которая имеет одинаковую длину для предложения любой длины, что позволяет нам сравнивать гистограммы разных предложений с помощью, например косинусного расстояния, или с помощью декартового расстояния, как мы и делали в предыдущем методе.
Воспользуемся этим и подумаем, что нам надо? Нам надо, чтобы гистограмма предложения «Бычок консервированный в соусе» была как можно более не похожа (далека в пространстве признаков) от предложения «Килька консервированная в соусе»:
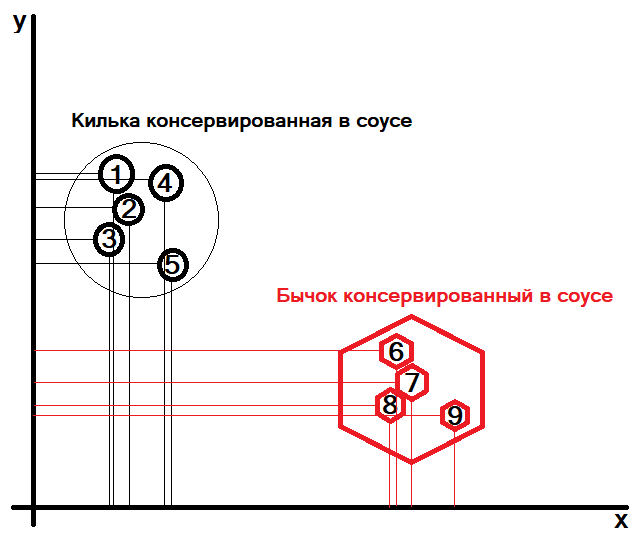
На данном графике изображены два множества.
Множество «Килька консервированная в соусе» имеет представителей:
- «Килька консерв. в соусе».
- «Килька консервир. в соусе».
- «Килька законсервированная в соусе».
- «Килька консервирован. в соусе».
- «Килька законсервир. в соусе».
Множество «Бычок консервированный в соусе» имеет представителей:
- «Бычок консерв. в соусе».
- «Бычок консервир. в соусе».
- «Бычок законсервированный в соусе».
- «Бычок законсервир. в соусе».
Использую декартову систему координат — для каждого представителя множества мы можем сделать расчет проекций их координат на ось X, и на ось Y.
Примечание: здесь приведена двумерная система координат (в которую спроецируем сам вектор предложения) только для демонстрации самой идеи. В реальных данных конечно, это будет n-мерная система координат, в которую будет проецироваться каждый n-мерный вектор предложений.
Получается список координат: (x0i, y0i) где i от 1 до 5 для множества «Килька консервированная в соусе».
И список координат: (x1i, y1i) где i от 1 до 4 для множества «Бычок консервированный в соусе».
Наша задача состоит в том, чтобы расстояния между представителями множества (x0i, y0i), и также между представителями множества (x1i, y1i) были меньше (внутри своих множеств), чем расстояния между представителями множества «Килька консервированная в соусе» и «Бычок консервированный в соусе».
Само расстояние будем считать как декартово расстояние:
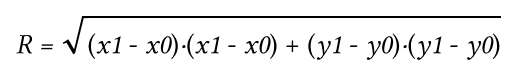
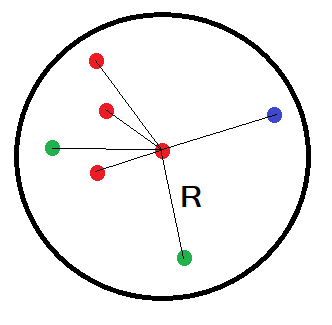
R — это некая метрика, которую мы и будем оптимизировать (нам нужно чтобы расстояние от центральной красной точки до остальных красных точек уменьшалось, а расстояния до зеленых точек и до синей точки увеличивалось).
x, y — это проекции координат представителей множеств на оси.
Как это будем делать?
Выбираем два предложения — «Килька консервированная в соусе», «Бычок консервированный в соусе». Далее из «Килька консервированная в соусе» формируем похожее предложение — «Килька консервир. в соусе» (или выбираем предложение из того же класса, что и «Килька консервированная в соусе»).
У нас получится триплет — якорь «Килька консервированная в соусе», позитивный пример «Килька консервир. в соусе» и негативный пример «Бычок консервированный в соусе». И просим наш алгоритм, чтобы он приблизил в признаковом пространстве якорь с позитивным примером и отдалил их от негативного примера, чтобы координаты якоря и положительного примера были все ближе, а координаты якоря и негативного примера были все дальше:
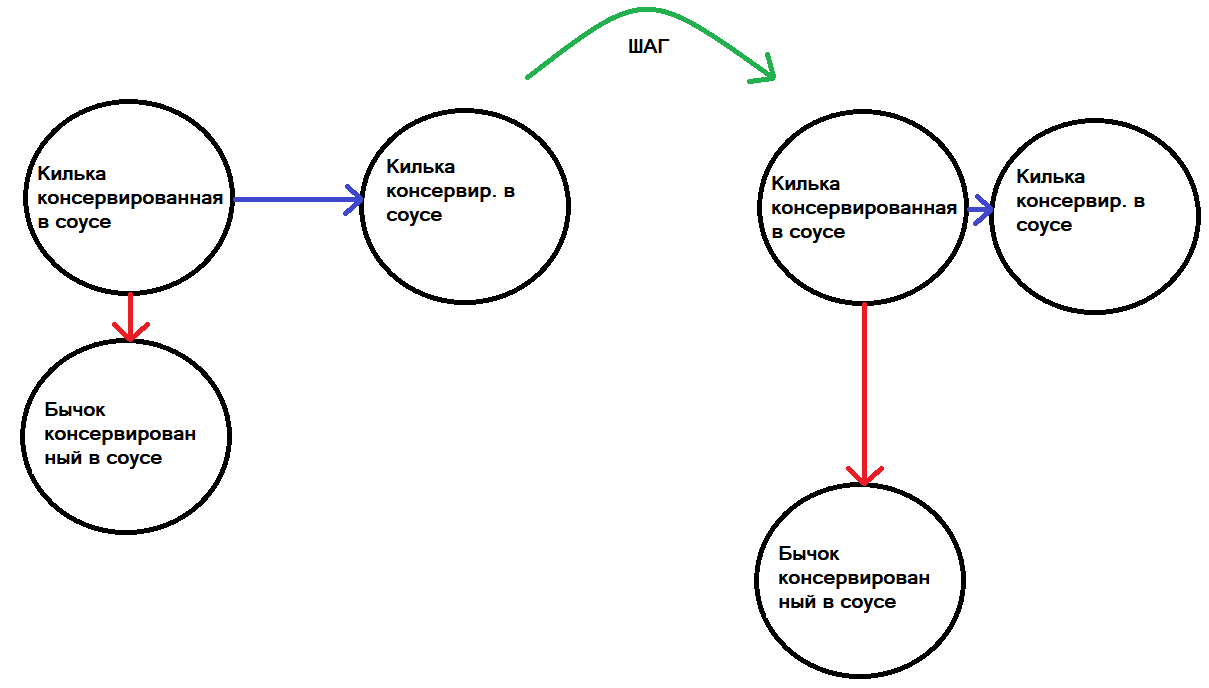
Синяя линия — это расстояние между якорем и положительным примером — нам нужно эту линию укорачивать.
Красная линия — это расстояние между якорем и негативным примером — нам нужно эту линию увеличивать.
Функция потерь
Функция потерь описывается как функция евклидова расстояния:
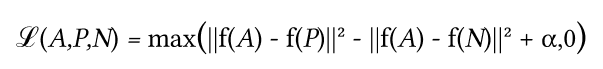
Где
A — наш якорь,
P — вход положительной выборки,
N — вход отрицательной выборки,
а альфа — некоторый запас, который мы используем, чтобы указать, когда семпл (в нашем случае вектор слова/предложения) стал слишком «легким» и мы больше не хотим регулировать веса из него.
Эту функцию потерь мы и будем использовать для расчета того, насколько наша модель хорошо относит тестируемое словосочетание к своему классу.
И так в цикле для всех пар предложений, а их будет много: пока алгоритм «скажет», что больше не могу пары якорь — негативный пример отдалять друг от друга.
Как это будем делать? Какой алгоритм использовать, чтобы проделывать такую работу — описывать не будем, это выходит за рамки данной статьи, однако, можно отметить, что это все тот же алгоритм градиентного спуска. Хотя можно применять и другие оптимизационные алгоритмы. Но на существующий момент, алгоритм градиентного спуска самый эффективный в части скорости и точности.
В результате мы получим модель, в которую можно подать гистограмму тестируемого предложения, а на выходе модели будет та же гистограмма, но в другом признаковом пространстве. И мы сможем по косинусному (или декартовому) расстоянию найти наиболее близкое словосочетание в базе справочника «Номенклатура».
Можно объяснить это на следующем примере: допустим, у нас есть два множества — «Килька консервированная в соусе» и «Бычок консервированный в соусе».
Элементы множества «Килька консервированная в соусе»:
Килька консервир. в соусе
Килька законсервированная в соусе
Килька консервирован. в соусе
Килька законсервир. в соусе
Килька законсервированная в соусе 20грамм
Килька законсервированная в соусе 30грамм
Килька законс. в соусе 30грамм
Килька конс. в соусе 20грамм
Килька конс. в соусе
Килька законсервированная в соусе 50грамм
Элементы множества «Бычок консервированный в соусе»:
Бычок консервир. в соусе
Бычок законсервированный в соусе
Бычок законсервир. в соусе
Бычок законсервированный в соусе 20грамм
Бычок законсервированный в соусе 30грамм
Бычок конс. в соусе
Бычок консер в соусе
Бычок законсервированный в соусе 50грамм
Строим для каждого предложения гистограмму и пропускаем через нейронную сеть. На выходе получим признаковое описание каждого предложения.
Построим двумерный график распределения:
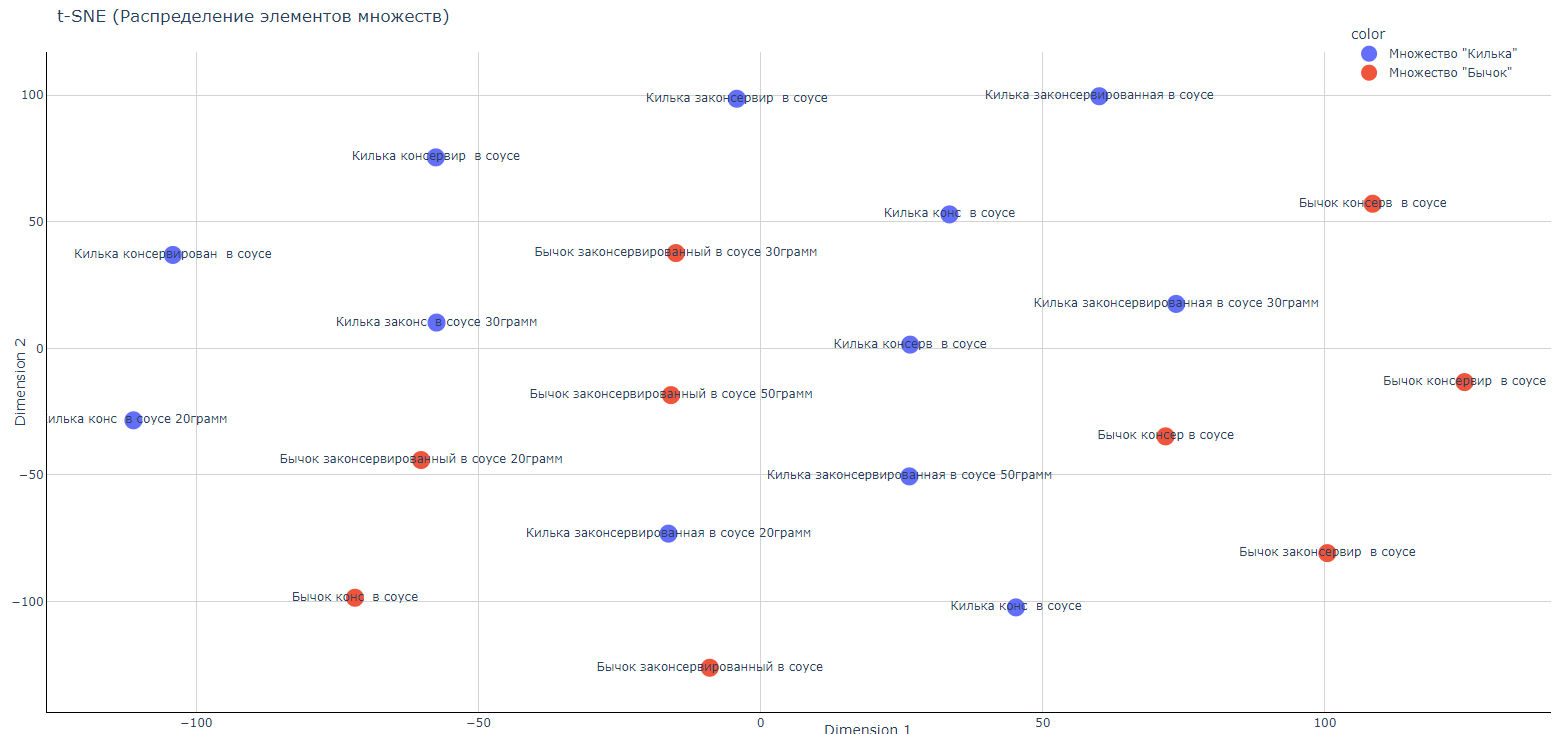
Рис. Представление множеств «Килька консервированная в соусе», «Бычок консервированный в соусе» в метрическом пространстве до оптимизации. Двумерное распределение.
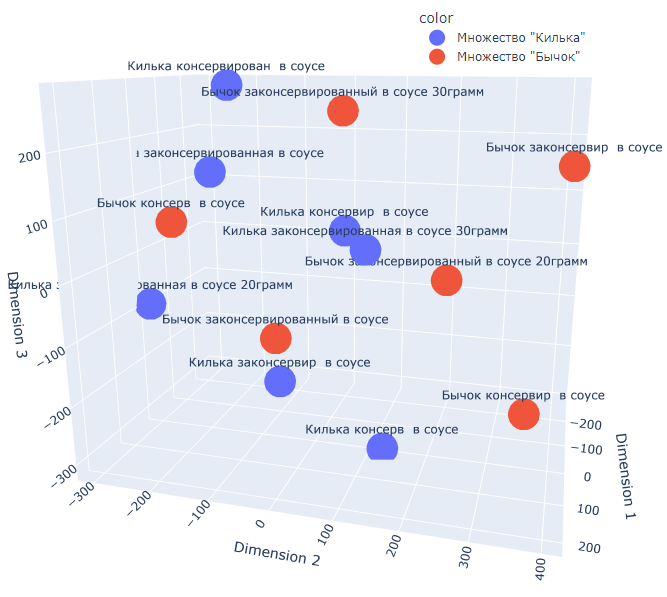
Рис. Представление множеств «Килька консервированная в соусе», «Бычок консервированный в соусе» в метрическом пространстве до оптимизации. Трехмерное распределение.
Из распределения видно, что элементы множества перепутаны между собой и даже переход к трехмерному пространству не помогает четко разделить множества между собой.
Матрица путаницы
Построим матрицу путаницы (confusion matrix).
Матрица путаницы представляет из себя таблицу, в которой показано насколько система путает классы. Т. е. на вход модели подаем какой-то элемент множества (например, «Килька»), а модель отвечает что это другой класс. Это ошибка модели.
Давайте возьмем все примеры каждого из 2-х классов и рассмотрим их троих ближайших соседей как форму предсказания; то есть, разделяет ли пример и его ближайшие соседи один и тот же класс?
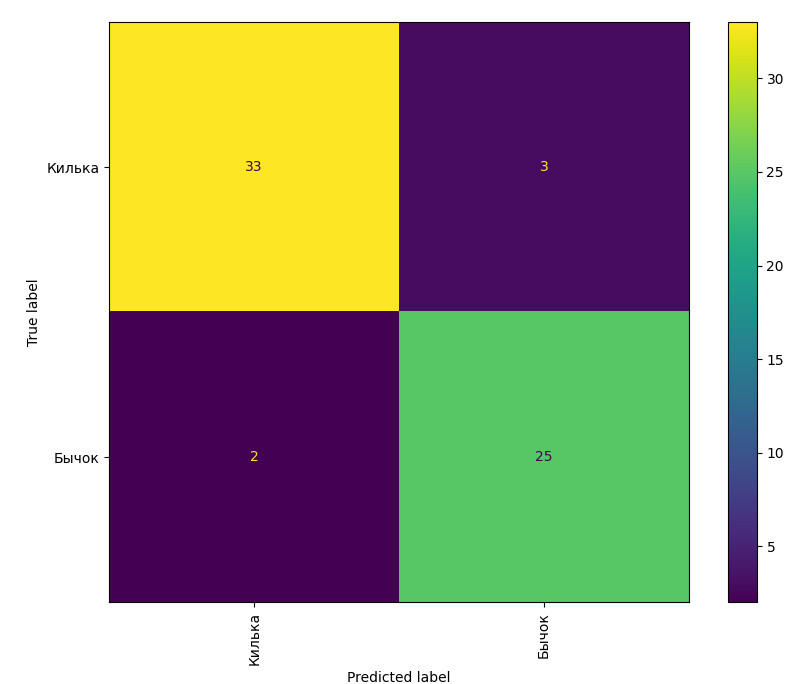
Рис. Матрица путаницы до оптимизации. Даже сейчас не все так оказалось плохо!
По вертикали отмечены истинные значения элементов множества. По горизонтали отмечены ответы модели.
Из представленной матрицы видим, что модель два раза неправильно отнесла к ближайшим соседям представителя класса «Бычок» представителей класса «Килька». Три раза тоже самое произошло для элементов класса «Килька» — среди ближайших представителей оказались представители класса «Бычок».
Попробуем обучить нашу нейронную метрическую сеть и построим графики распределения для наших множеств.
Представление множеств «Килька консервированная в соусе», «Бычок консервированный в соусе» в метрическом пространстве после нахождения параметров модели.
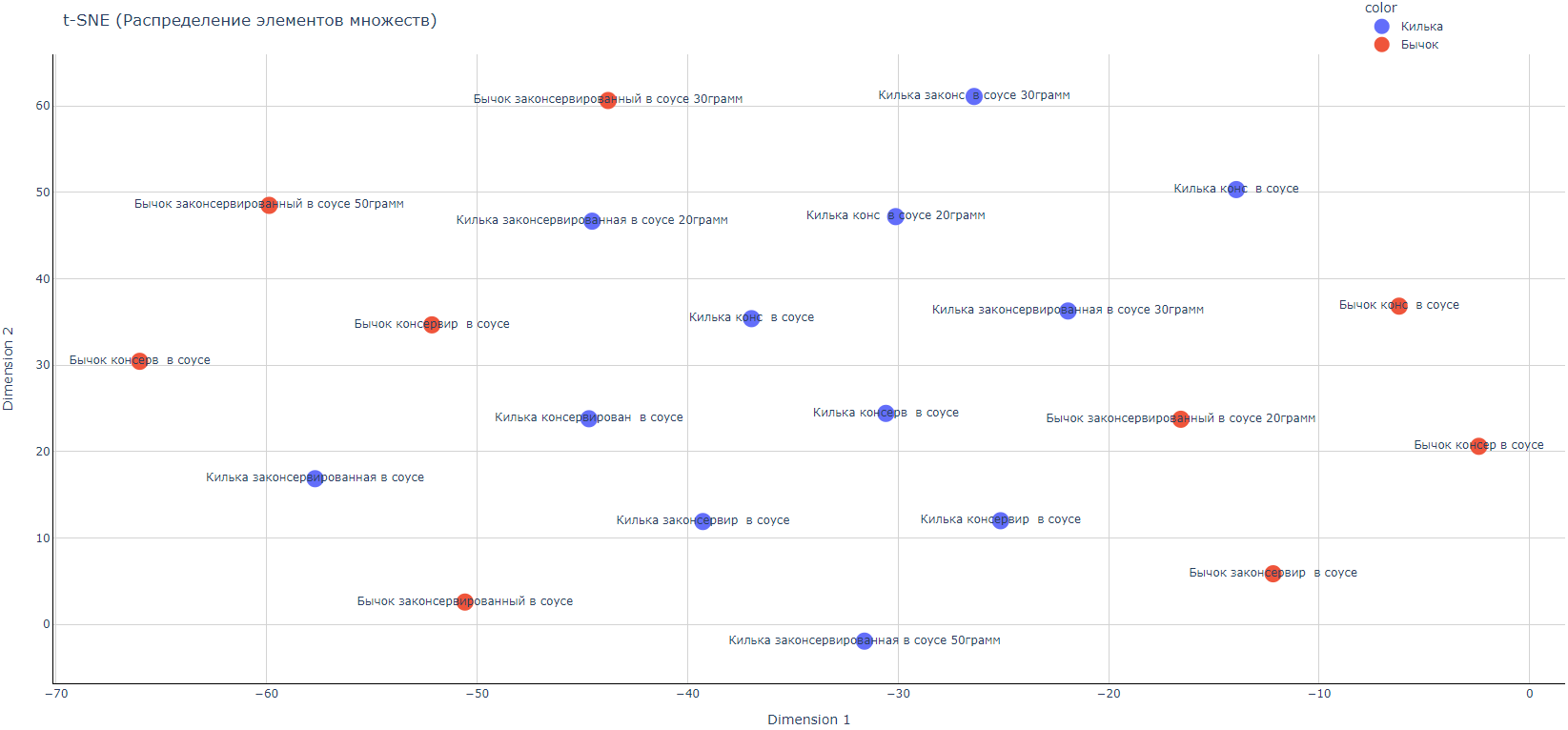
Рис. Представление множеств «Килька консервированная в соусе», «Бычок консервированный в соусе» в метрическом пространстве после оптимизации. Двумерное распределение.
T-SNE (tsne) — это алгоритм уменьшения размерности, который хорошо подходит для визуализации многомерных данных. Это название расшифровывается как t-распределенное стохастическое вложение соседей. Идея состоит в том, чтобы встроить многомерные точки в маломерные таким образом, чтобы учитывалось сходство между точками.
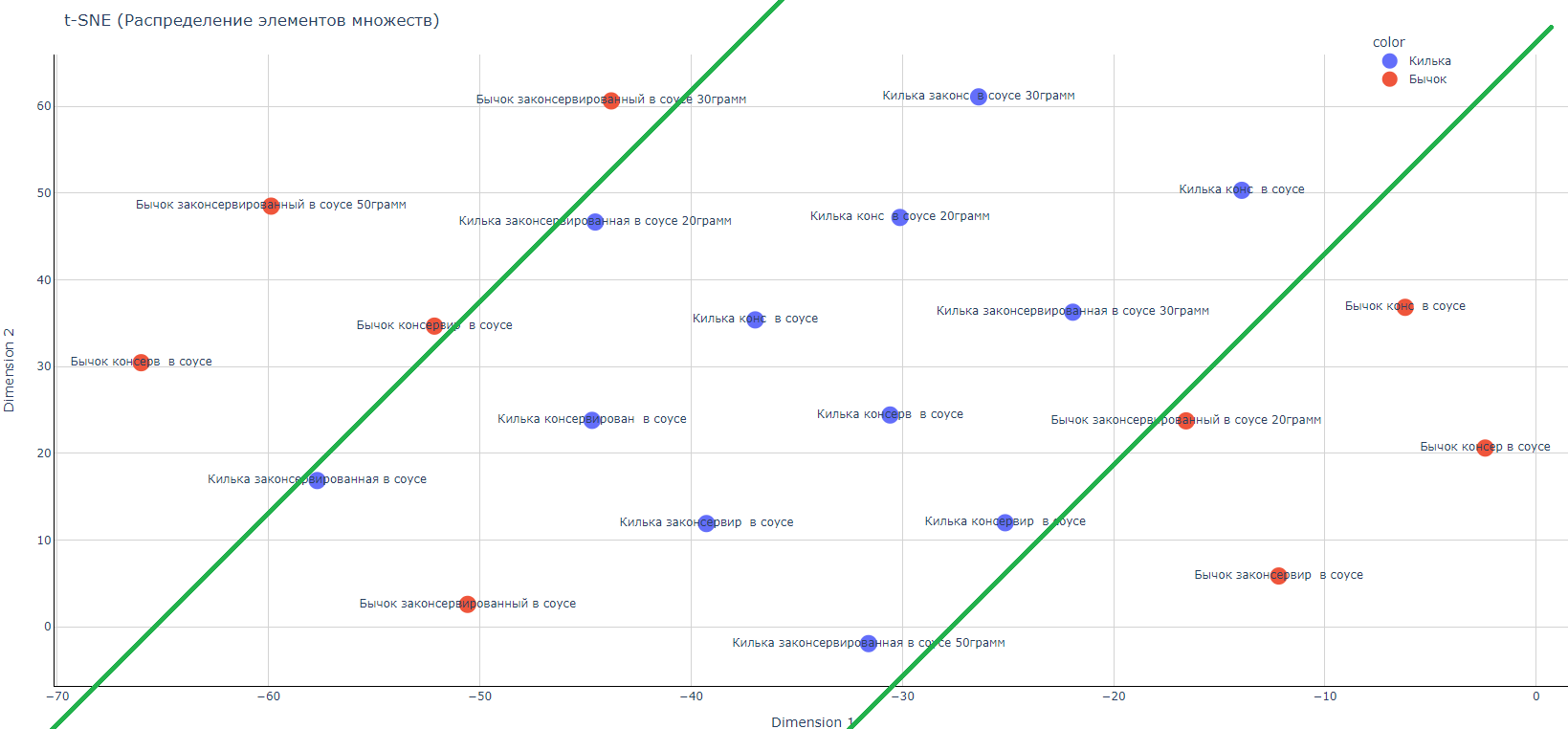
Рис. После оптимизации мы можем построить разделяющие линии, которые отделяют два класса друг от друга.
Т. е. мы смогли улучшить нашу модель. Есть только одна ошибка в нашем разделении — это красный кружок «Бычок консервированный в соусе». Но это возможно исправить путем модификации модели и наличия большего числа данных:
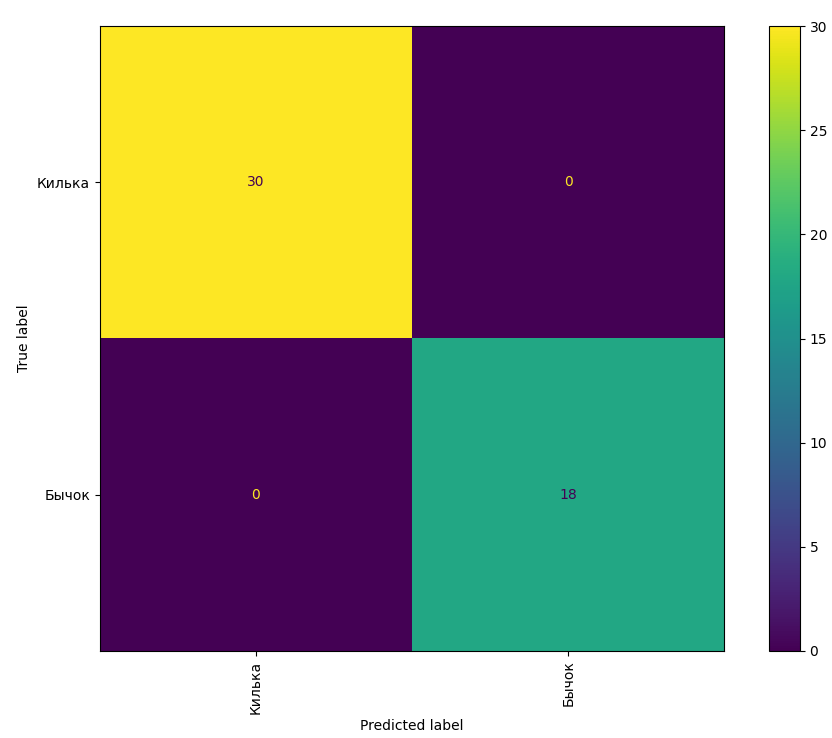
Рис. Матрица путаницы после оптимизации.
Видим, что применение оптимизации позволило со стопроцентной вероятностью корректно относить каждый элемент множества к своему множеству. Здесь уместно сделать важное замечание — это представлены результаты на тренировочных данных, чтобы показать саму идею работы алгоритма. Далее мы посмотрим как эта модель работает уже в режиме обучения на тренировочных данных, а тестирование на данных, которых не было предъявлено модели в режиме обучения, или на так называемых тестовых данных.
Модель «Наивный байесовский классификатор»
Наивный байесовский классификатор — это семейство алгоритмов классификации, которые принимают одно допущение: каждый параметр классифицируемых данных рассматривается независимо от других параметров класса.
В нашей задаче, конечно, это не совсем так, потому что появление определенного биплета иногда зависит от появления другого биплета. Но на то он и наивный :)
Примечание:
Конечно, биплеты семантически связаны друг с другом. Например, после биплета с окончанием на гласную букву реже идет биплет с началом на гласную букву. И наоборот, биплет с окончанием на согласную букву — чаще следующий биплет идет с началом на согласную букву: например — предсказать- после биплета дс идет биплет ка. Но это зависит от контекста тестового сообщения.
По сути, теорема позволяет нам предсказать класс на основании набора параметров, используя вероятность:

Уравнение читается следующим образом:
Вероятность [выявления] класса А на основании параметров 1 и 2 — это дробь.
Числитель дроби — это вероятность параметра 1, принадлежащего классу А, умноженная на вероятность параметра 2, принадлежащего классу А, умноженная на вероятность класса А.
Знаменатель — это вероятность параметра 1 умноженная на вероятность параметра 2.
Т. е. нам просто необходимо составить частотные таблицы для каждого наименования справочника номенклатуры.
Пример для расчета
(источник datascientist.one/naive-bayes/):
У нас есть тренировочный набор данных о 1000 фруктах.
Фрукт может быть бананом, апельсином или каким-нибудь другим — это классы.
Фрукт может быть длинным, сладким или желтым — это параметры, для нас это будут значения-счетчики гистограммы (тут есть маааленький подводный камень :) — о нем далее).
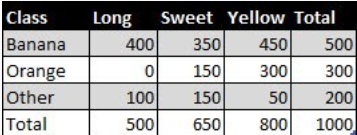
Из 500 бананов 400 длинные, 350 сладкие и 450 желтые.
Среди 300 апельсинов нет ни одного длинного, но оказалось 150 сладких и 300 желтых.
Из оставшихся 200 фруктов 100 оказались длинными, 150 сладкими и 50 желтыми.
Если мы получим только параметры — длину, сладость и цвет фрукта (не зная его класса), то сможем вычислить вероятность того, что фрукт окажется бананом, апельсином или чем-то другим.
Предположим, что неизвестный фрукт длинный, сладкий и желтый.
Для вычисления вероятности нужно проделать 4 простых шага:
Шаг 1: Чтобы вычислить вероятность того, что неизвестный фрукт — это банан, давайте сначала решим, похож ли этот фрукт на банан. Вот как вычисляется вероятность класса «Банан» на основании параметров «длинный», «сладкий», «желтый»:
P(Banana|Long, Sweet, Yellow)
Выглядит точно так же как уравнение, описанное выше.
Шаг 2: Начнем с числителя и подставим все значения в уравнение:
P(Sweet|Banana) = 350/500 = 0.7
P(Yellow|Banana) = 450/500 = 0.9
P(Banana) = 500/1000 = 0.5
Перемножив значения (согласно уравнению), мы получим:
0.8 × 0.7 × 0.9 × 0.5 = 0,252
Шаг 3: Проигнорируем знаменатель, поскольку он будет одинаковым для всех последующих вычислений.
Шаг 4: Проделаем те же вычисления для других классов:
P(Other|Long, Sweet, Yellow) = 0.01875
Поскольку 0,252 больше, чем 0,01875, то наивный байесовский алгоритм классифицирует этот длинный, сладкий и желтый фрукт как банан.
Этот метод требует обучения, поскольку алгоритм использует размеченный набор данных для построения таблицы.
Когда частотные таблицы уже вычислены, классификация неизвестного фрукта включает в себя только вычисления вероятностей для всех классов, а затем выбор наибольшей вероятности.
Несмотря на простоту, наивный байесовский алгоритм может быть удивительно точным. Например, было установлено, что он может быть успешно применен для фильтрации спама.
Примечание:
В нашем случае, гистограмма разреженная. Необходимо придумать режим обхода проблемы нулевой частоты. Чтобы решить эту проблему, мы можем использовать технику сглаживания. Один из самых простых методов сглаживания называется оценкой Лапласа.
Объясним это немного более подробно.
Проблема нулевой частоты
Одним из недостатков наивного байесовского алгоритма является то, что если класс и значение параметра не встречаются вместе, то оценка вероятности, рассчитываемой с использованием частот, будет равна нулю — т.к. использую наивное предположение что наши признаки независимы, то мы производим перемножение вероятностей — и если хотя бы одна из вероятностей равна нулю, то и все произведение будет равно нулю: Пpi = 0.7 × 0.2 × 0.0 × ..... = 0. В итоге после перемножения всех вероятностей мы получим ноль.
В байесовской среде было найдено решение этой проблемы нулевой частоты: к каждой комбинации класса и значения параметра добавлять единицу, когда значение параметра нулевое.
Предположим, у нас есть такой набор данных:

P(TimeZone=US|Spam=yes)=10/10=1
P(TimeZone=EU|Spam=yes)=0/10=0
Появляется нулевое значение, поэтому при вычислении вероятностей добавляем единичку к каждому значению этой таблицы:

P(TimeZone=US|Spam=yes)=11/12
P(TimeZone=EU|Spam=yes)=1/12
Вот так мы избавляемся от нулевой вероятности.
Применение наивного байесовского классификатора для дублей номенклатуры
В нашем случае, вместо фруктов — это наименование из существующего справочника номенклатуры или наименование вида номенклатуры, как более общее свойство. Например, вид номенклатуры «Алюминий» — все изделия, относящиеся к алюминиевым изделиям. А вместо цвета, длины, вкуса фрукта — это значения гистограммы (биплеты).
В результате после расчета гистограммы мы можем программно «пробежаться» по всей частотной таблице и после вычисления частот произвести расчет вероятностей «схожести» нашего проверяемого предложения каждому наименованию из справочника номенклатуры — и взять максимум. Это и будет наиболее похожее наименование. И если вероятность >= заданного значения, то мы нашли двойника введенного наименования.
Применимо к нашему случаю — используем базу данных, на которой обучалась нейронная сеть в разделе статьи про «нейросетевую метрическую модель».
Еще чуть-чуть теории — теорема Байеса утверждает следующее отношение, учитывая переменную класса y и зависимый вектор признаков x1 через xn:
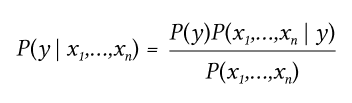
Используя наивное предположение об условной независимости:
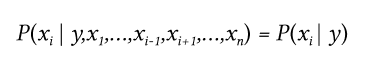
Для всех i, это отношение упрощается до:
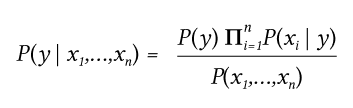
С P(x1,...,xn) является константой с учетом входных данных, мы можем использовать следующее правило классификации:
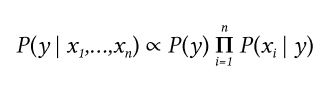
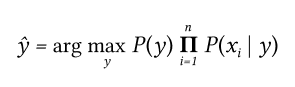
И мы можем использовать оценку Maximum A Posteriori (MAP) для оценки 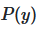 , а также
, а также 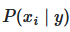 .
.
Где 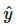 - предсказанный моделью класс.
- предсказанный моделью класс.
Различные наивные байесовские классификаторы различаются в основном предположениями, которые они делают относительно распределения 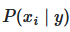 .
.
Мы будем использовать «ComplementNB» — из
ComplementNB — реализует наивный байесовский алгоритм дополнения (CNB).
CNB — это адаптация стандартного полиномиального наивного байесовского алгоритма (MNB), который особенно подходит для несбалансированных наборов данных. В частности, CNB использует статистику из дополнения каждого класса для вычисления весов модели. Изобретатели CNB эмпирически показали, что оценки параметров для CNB более стабильны, чем для MNB. Кроме того, CNB регулярно превосходит MNB (часто со значительным отрывом) в задачах классификации текста.
Модель «Нечеткая логика»
Нечеткая логика — это форма многозначной логики, в которой истинностным значением переменных может быть любое действительное число от 0 до 1. Он используется для обработки концепции частичной истинности, где значение истинности может варьироваться от полностью истинного до полностью ложного. Напротив, в булевой логике истинностными значениями переменных могут быть только целочисленные значения 0 или 1.
С помощью нечеткой логики можно определить такие понятия, как «высокая температура», «средний рост», «большой город».
Нечетким множеством А, определенном в некотором непустом пространстве Х называется множество пар:
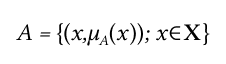
Где:
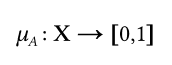
— это функция принадлежности нечеткого множества.
Эта функция приписывает каждому элементу x, степень принадлежности к нечеткому А.
Метод нечеткого управления Такаги-Сугено
Допустим, у нас есть база правил для нечеткой системы с двумя входами (гистограмма с двумя ячейками — для упрощения описания) и одним выходом (фактически, индекс предложения в справочнике «Номенклатура»).
Тогда у нас будут обучающие пары:
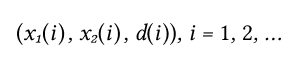
Где x1(i), x2(i) — входные значения (сигналы) подаваемые на вход.
d(i) — ожидаемое (эталонное) значение.
Задача состоит в том, чтобы сконструировать такой модуль, который при подаче входных сигналов выдавал бы наиболее корректные выходные сигналы (имеющие наименьшую погрешность).
Разделение пространств входных и выходных сигналов
Сначала используя обучающую выборку найдем минимальные и максимальные значения для x1 и x2:
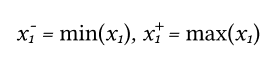
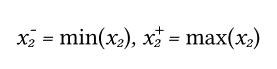
Также и для эталонного сигнала:
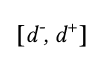
Каждый определенный таким образом интервал разделим на 2N+1 отрезков, причем значение N для каждого сигнала подбираем индивидуально.
Отдельные области обозначим так: Mn (малые n), S (средний), Dn (большие n):
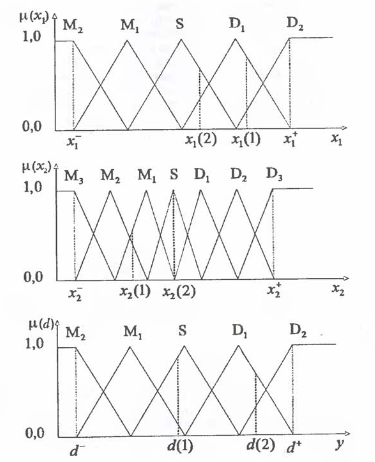

Мы разбили сигнал x1 на 5 областей (N=2), сигнал x2 на 7 областей (N=3). Это были входные сигналы.
Также мы разбили выходной сигнал на 5 областей (N=2).
Каждая функция принадлежности имеет треугольную форму. Но нам ничего не мешает выбрать другую форму функции принадлежности как в целом для всех сигналов, так и для каждого сигнала по отдельности.
Построение нечетких правил на основании обучающих данных
Вначале определим степени принадлежности обучающих данных (x1(i), x2(i) и d(i)) к каждой области. Эти степени будут выражаться значениями функций принадлежности соответствующих нечетких множеств для каждой группы данных.
Например: степень принадлежности x1(1) области D1 равно 0.8, к области D2 равно 0.2, а к остальным областям ноль.
Сопоставим обучающие данные (x1(i), x2(i) и d(i)) каждой области и возьмем по максимальному значению.
В итоге для каждой пары обучающих данных можно записать одно общее правило:
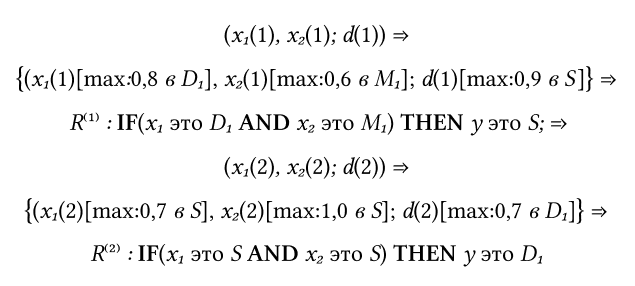
Приписывание каждому правилу степени истинности
Как правило, в наличии имеется большое количество пар обучающих данных. По каждой из них может быть сформулировано одно правило, поэтому возможны случаи, когда некоторые правила будут противоречивыми. Это относится к правилам с одним и тем же условием, но с разными выводами. Метод решения достаточно простой — выбираем то правило, у которого степень истинности максимальная. Таким образом, мы устраним противоречивые выводы (следствия) и бонусом получим то, что база правил у нас уменьшится.
Например, для правила вида:
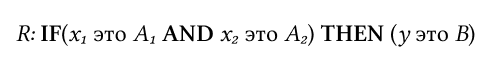
Степень истинности будет:
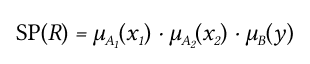
Таким образом, первое правило имеет степень истинности:
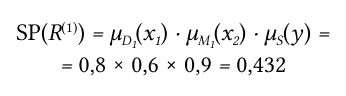
А второе правило:
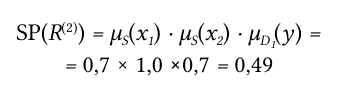
Создание базы нечетких правил
База правил представляет из себя таблицу вида:
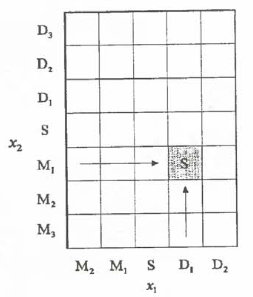
Соответствующее правило вычисляется следующим образом:
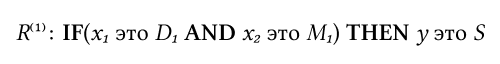
Если имеются несколько одинаковых посылов, но с разным выводом, то берем то правило, у которого максимальная степень истинности.
Дефаззификация
Наша конечная задача заключается в определении с помощью базы правил отображения:
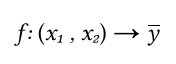
Где 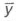 - это предсказание нашей модели
- это предсказание нашей модели
Чтобы вычислить 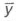 при воздействии
при воздействии 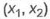 с учетом базы правил нам нужно выполнить операцию дефаззификации.
с учетом базы правил нам нужно выполнить операцию дефаззификации.
Сначала мы определяем степень активности k-го правила:
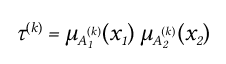
Например, для первого правила будет равно:
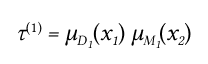
Для расчета выходного значения 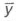 воспользуемся способом дефаззификации по среднему центру:
воспользуемся способом дефаззификации по среднему центру:
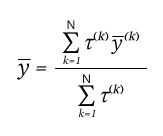
В итоге мы имеем предсказанное предложение из базы справочника «Номенклатура».
Промежуточный вывод
При всей очевидности постановки задачи оказывается, что без математического аппарата всерьез решать данный класс задач попросту невозможно. Безусловно можно латать дыры и закрывать частично проблематику. Однако, чтобы решить задачу во всей ее полноте необходимо применять математику.
Когда мы говорим о полноте решения тут тоже следует делать это с аккуратностью, поскольку мы видим и знаем только часть коллизий и, конечно, возможны ситуации, когда возникают новые условия, когда инвариантный признак перестает обладать инвариантностью, как, например, в случае появления латинских символов, которые мы не учитывали в исходном алфавите. Или когда одни символы становятся намного более значимыми, чем другие, как в случае с цифрами.
В следующей статье рассмотрим практическое применение нейронных сетей, наивного байесовского классификатора, нечеткой логики, и разберем код, реализующий данный функционал. А также посмотрим как можно весь этот математический зоопарк подружить с программами 1С :).
От экспертов «1С-Рарус»
























