Оглавление
В первой части статьи мы с необходимой для решения задачи детальностью разобрали теоретическую область изучаемого вопроса, разобрались с методической областью: откуда берутся дубли номенклатуры в справочнике, какие их виды бывают, из-за чего возникают, как с этим можно бороться — административные и математические методы решения данной проблематики.
В этой статье разберем практическую часть применения рассмотренных ранее методов и программный функционал. А также посмотрим как можно весь этот математический зоопарк подружить с 1С. :)
Немного вспомним о чем мы говорили в прошлой статье:
Мы работаем со справочником «Номенклатура», в котором нам необходимо найти одинаковые (с заданной числовой мерой похожести) слова/предложения.
Слова/предложения мы договорились разбивать на биплеты и формировать из них гистограммы для инвариантности преобразования при перестановке слов в предложениях.
Мы научились находить похожие слова/предложения, рассчитывая косинусную дистанцию между словами/предложениями и используя эту числовую меру выносить суждение — насколько похожи/не похожи слова/предложения.
Итак, давайте рассмотрим четыре очень интересных математических метода, их теоретическую часть, программную реализацию для трёх из них и обсудим полученные результаты.
Нейросетевая «Метрическая модель»
Нейро́нная сеть (также искусственная нейронная сеть, ИНС, или просто нейро́сеть) — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге, и при попытке смоделировать эти процессы. Первой такой попыткой были нейронные сети У. Маккалока и У. Питтса. После разработки алгоритмов обучения получаемые модели стали использовать в практических целях: в задачах прогнозирования, для распознавания образов, в задачах управления и др.
Метрика — фактически, численное значение — разница между числовыми характеристиками элементов множества, которую можно померить.
Допустим, у нас есть корзина яблок разного веса. Множество — это яблоки веса от mмалое до mбольшое, а элементы множества — это сами яблоки в корзине. Получается A = {x0, x1, x2, ..., xn}.
Где:
A — это множество, содержащее в себе все возможные яблоки, а x0 — это яблоко с весом (допустим) 80 грамм, x1 — это яблоко с весом (допустим) 85 грамм и т. д.
n — это размер множества.
Тогда мы можем ввести евклидову метрику как функцию расстояния в метрическом пространстве между xi и xj элементами множества:
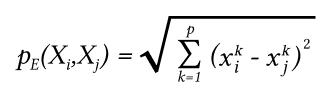
Это и есть как раз численное значение — метрика расстояния между элементами множества.
Применительно к нашей задаче, поиску наиболее похожих предложений для искомого предложения, множество — это множество гистограмм предложений, а метрика — это численное значение косинусного подобия внутри множества между всеми элементами множества.
Скалярное произведение векторов
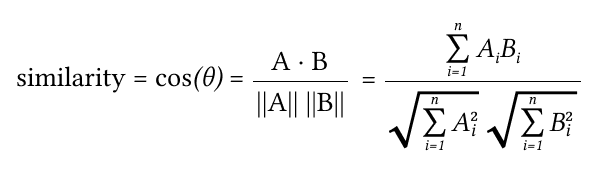
Где А и B — это два вектора (в нашем случае гистограммы предложений).
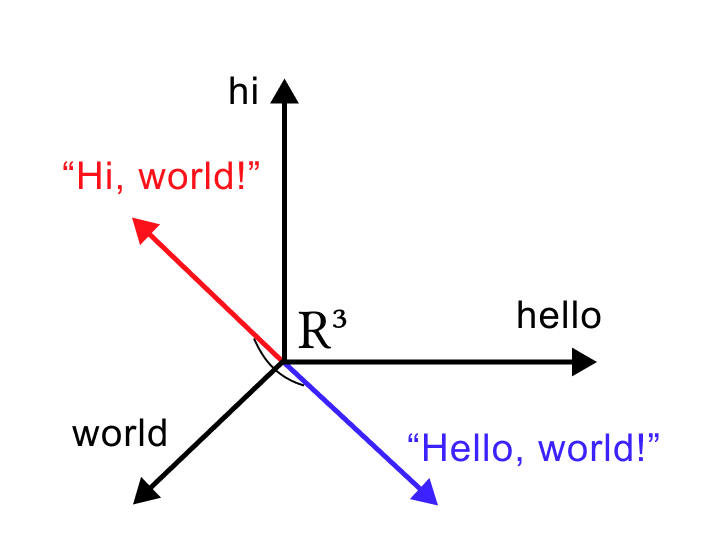
Косинусное подобие (сходство) — это показатель, используемый для измерения того, насколько похожи предложения независимо от их размера. Математически он измеряет косинус угла между двумя векторами, проецирующими в многомерное пространство.
Возвращаясь к нашей задаче.
Пусть нам дан справочник номенклатуры со следующим набором данных:
| Наименование группы номенклатуры | Количество элементов |
|---|---|
| Алюминий | 500 |
| Базальт | 5 |
| Бронза | 6 |
| БРО | 2 |
| БрХ | 4 |
| Латунь | 88 |
| Медь | 55 |
| Лист нержавеющая | 4 |
| Сталь нержавеющая | 942 |
| Сталь оцинкованная | 246 |
| Паронит | 31 |
| Сталь | 606 |
| Стеклотекстолит | 23 |
| ТМКЩ | 21 |
| Титан | 55 |
| Труба | 32 |
| Уголок сталь | 32 |
| Фторопласт | 6 |
Все элементы собираются в группы, пример:
Группа «алюминий»:
- Алюминий 1105АН 1.5 × 1500 × 3000 мм;
- Алюминий А5М 2,5 × 1500 × 3000 мм;
- Алюминий А5М 3 × 500 × 1200 мм.
Группа «бронза»:
- Бронза 0.8 × 300 × 900 мм;
- Бронза БрБ2 ДПРНМ 1 × 250 × мм.
и т. д.
График распределения для данных без оптимизации
T-SNE (tsne) — это алгоритм уменьшения размерности, который хорошо подходит для визуализации многомерных данных. Название расшифровывается как t-распределенное стохастическое вложение соседей. Идея состоит в том, чтобы встроить многомерные точки в маломерные таким образом, чтобы учитывалось сходство между точками.
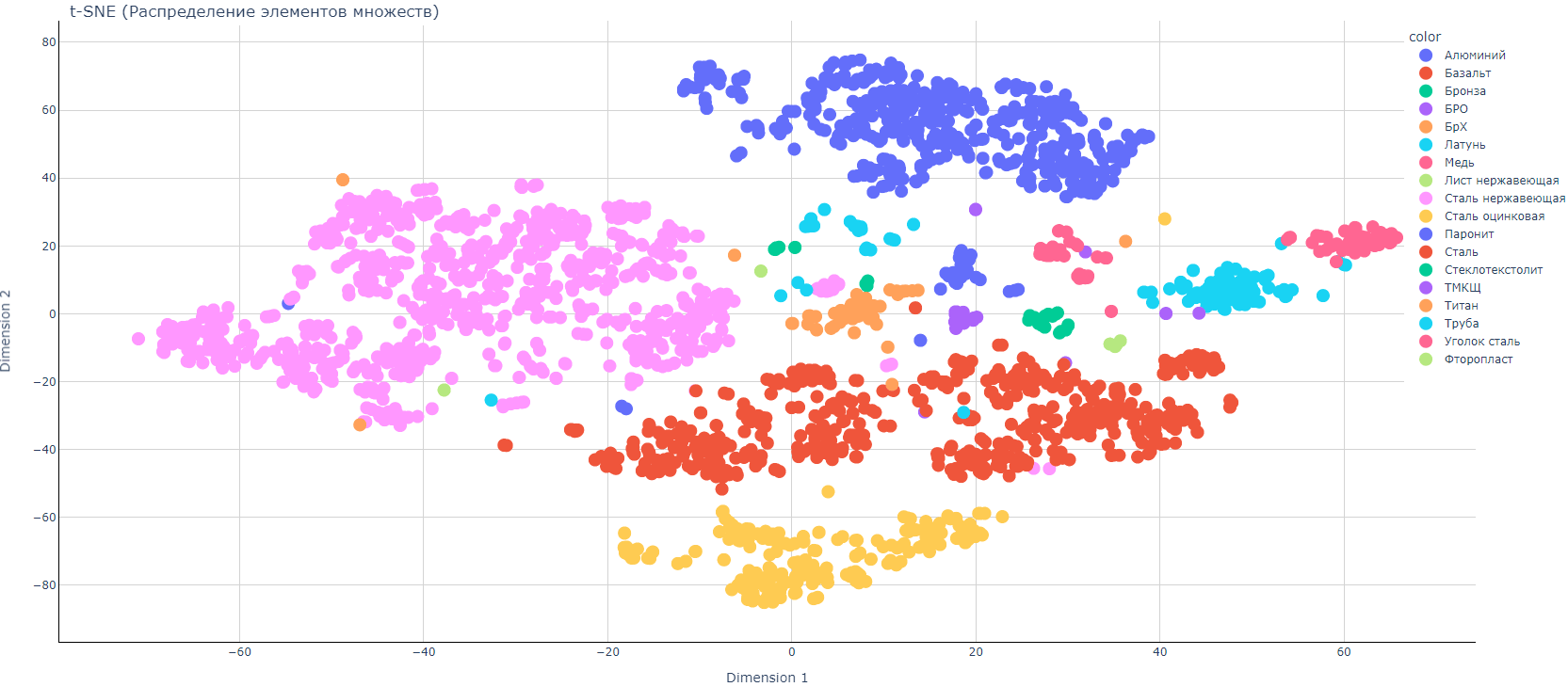
В принципе, в структуре данных уже хорошо просматривается выделенные классы, так что выбранный нами метод разбиения на биплеты и перевод в гистограммное представление оправдывает себя.
Правильный выбор признаков имеет решающее значение для построения качественной модели.
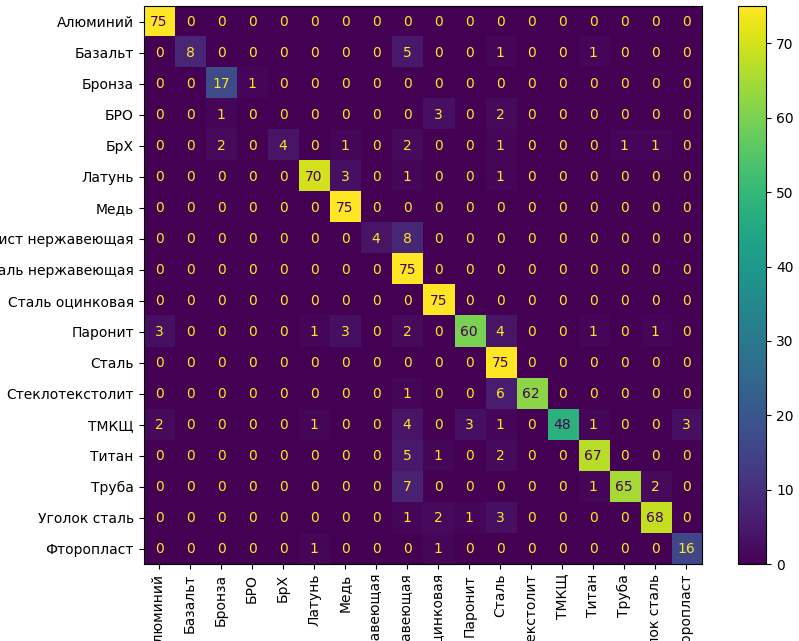
Видим, что на на главной диагонали матрицы путаницы находится основное число элементов. Т. е. наша модель даже без оптимизации уже хорошо будет работать. Максимальный процент ошибки между «Лист нержавеющий» и «Сталь нержавеющая». Т. е. модель путает эти два класса между собой, что в принципе объяснимо — в обоих предложениях присутствует слово «нержавеющая». Также модель путает класс «Труба нержавеющая» и класс «Сталь нержавеющая».
Проводим оптимизацию
Примечание
В понятие «оптимизация» мы вкладываем тот смысл, что модель должна уменьшить числовое значение используемой нами меры расстояния между записями относящимися к одной номенклатурной группе и увеличить числовое значение используемой нами меры расстояния между записями относящимися к разным номенклатурным группам. см. первую статью.
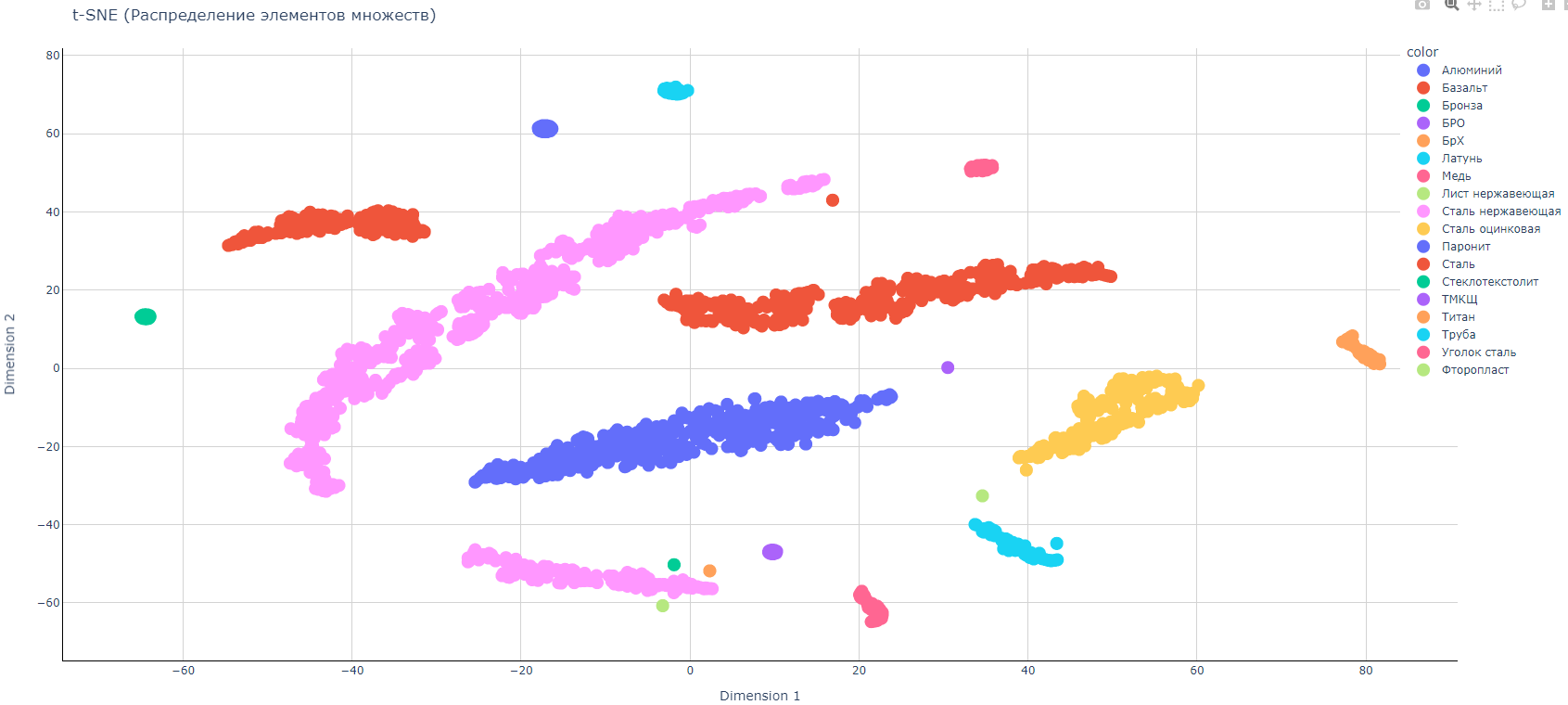
Видна четкая кластеризация данных по своим «облачкам» — и эти облачка удалены друг от друга.
На тренировочных данных модель показала очень хорошие результаты — модель путает только класс «БРО» со «Сталь нержавеющая» и «Сталь».
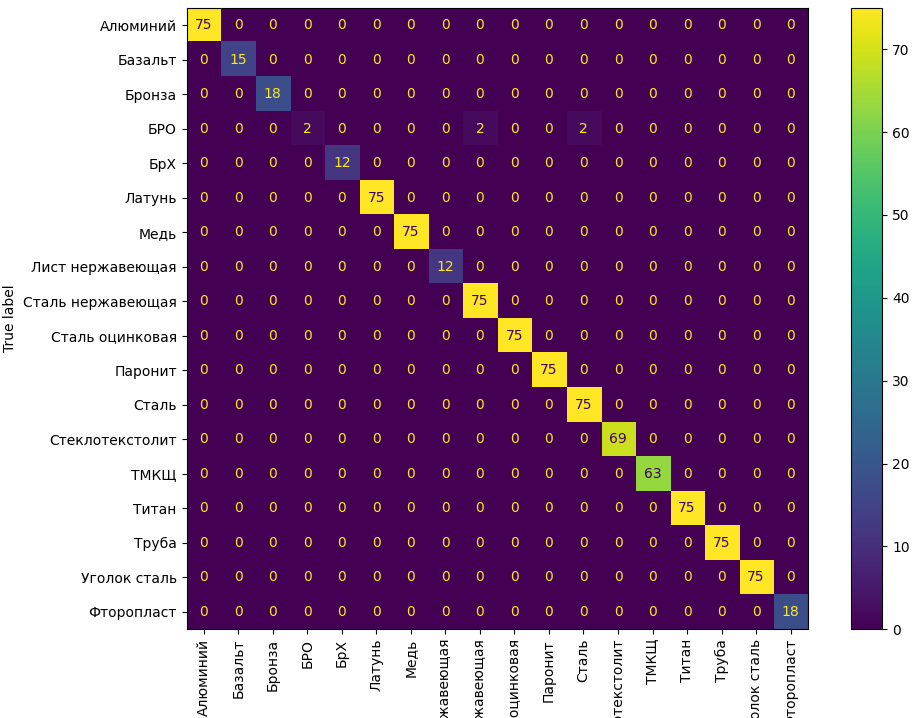
Проверим на тестовых данных.
Графики распределения до оптимизации:
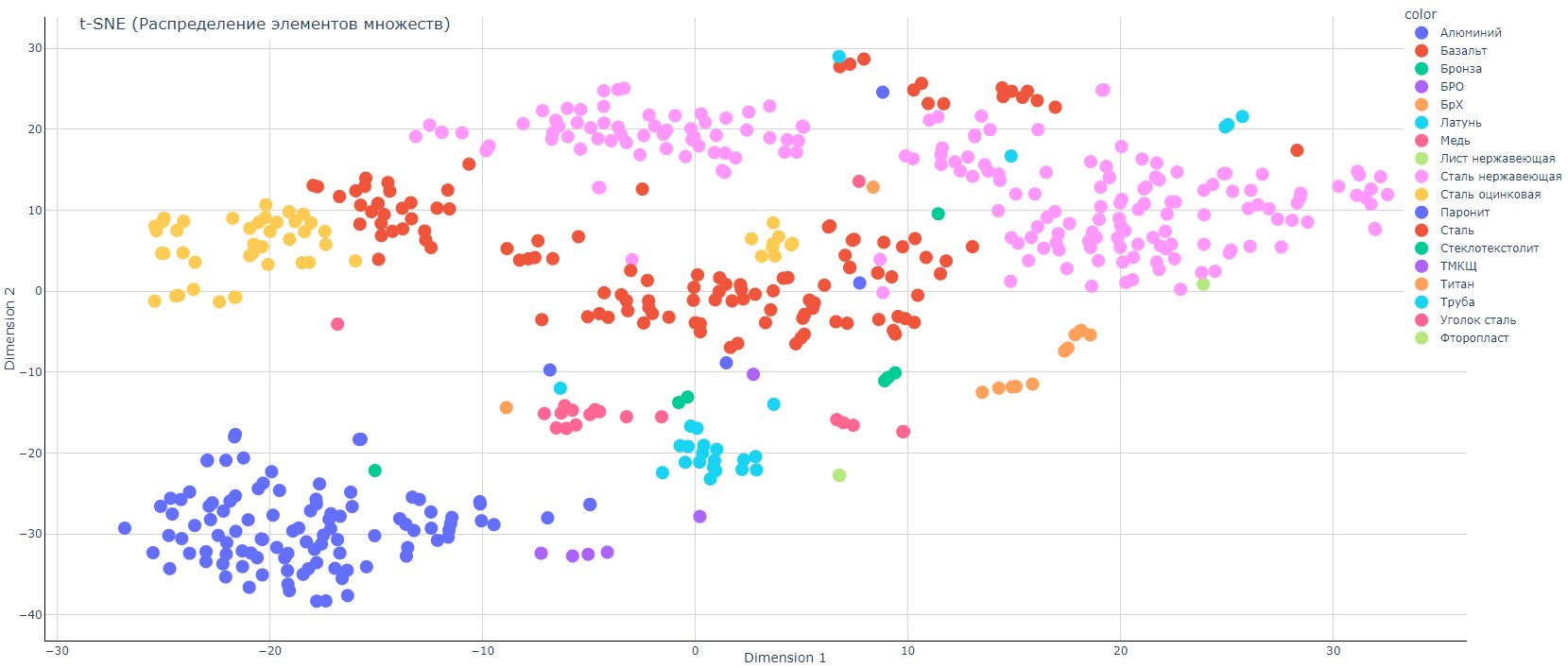
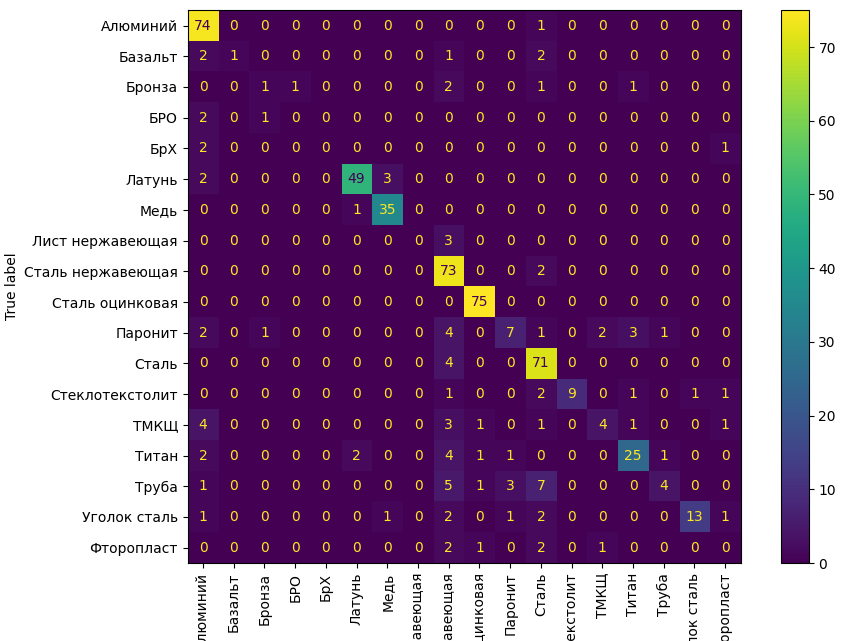
Не все так уж и плохо, честно говоря. Модель, хоть и с некоторым процентом ошибки, но хорошо разделяет представителей классов. Но нет предела совершенству. Оптимизируем на обучающем множестве, а проверяем на нашем тестовом отложенном множестве.
Графики распределения после оптимизации:
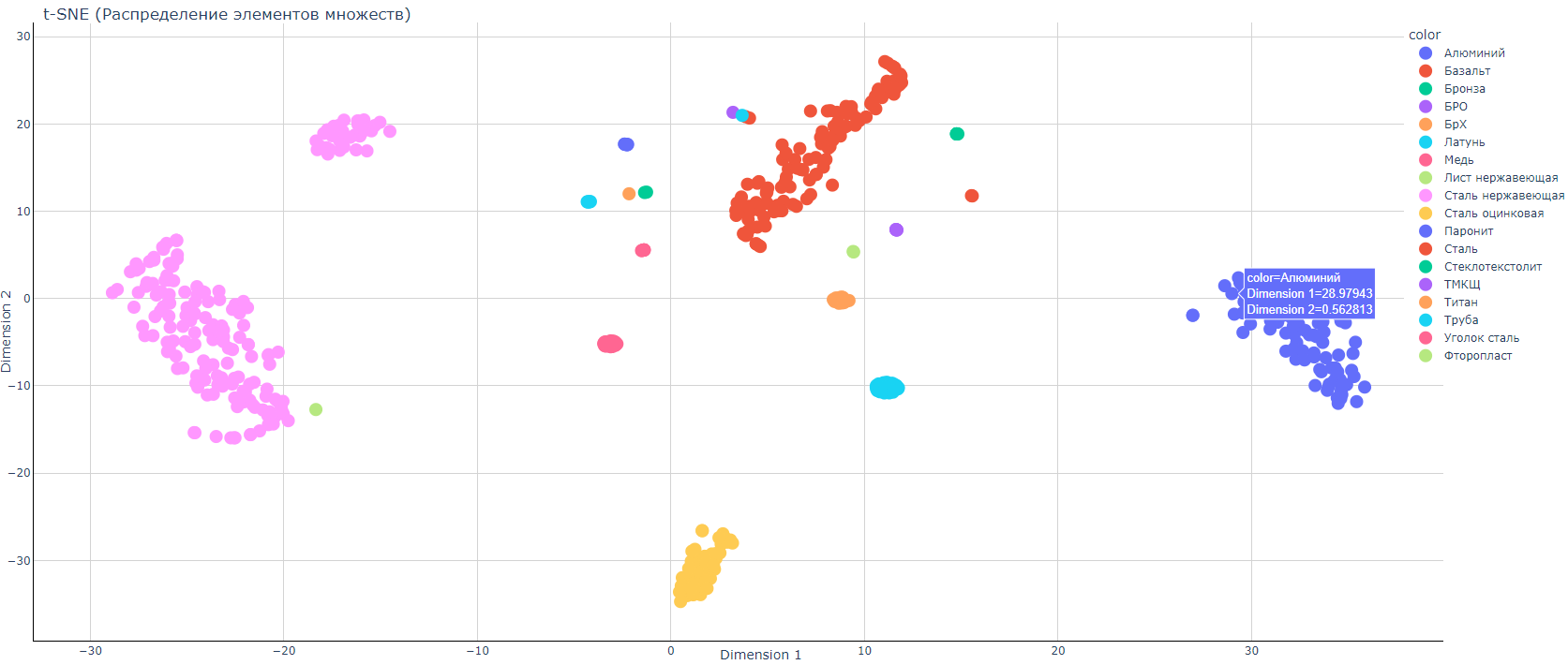
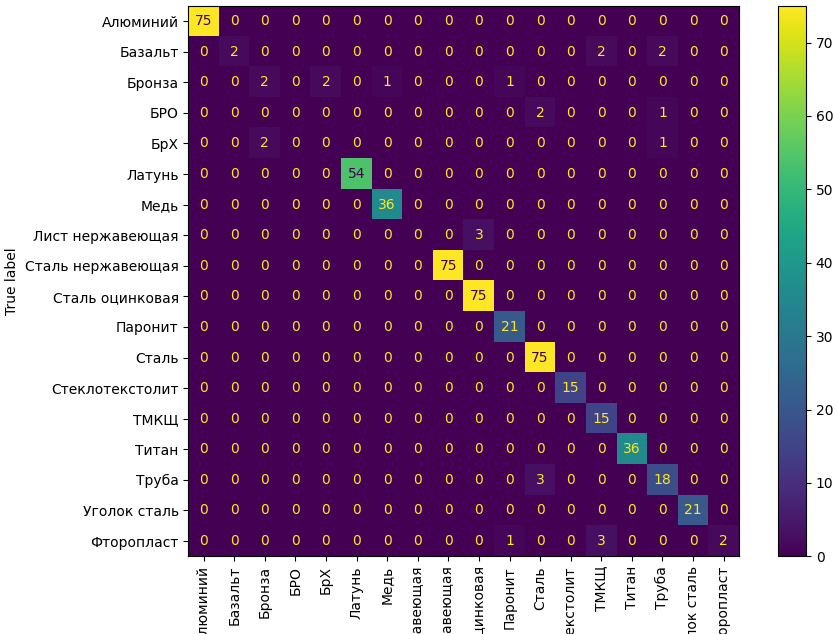
Из приведенных графиков видно, что и на тестовых данных (которые не участвовали в обучении) оптимизация модели привела к существенному улучшению качества ответа модели.
Составим сравнительные таблицы метрик
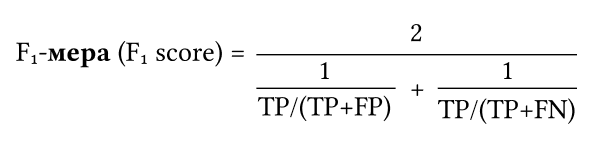
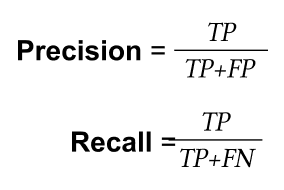
Balanced accuracy — сбалансированная точность (сбалансированная точность дает нам возможность оценить насколько хорошо модель способна предсказывать оба класса).
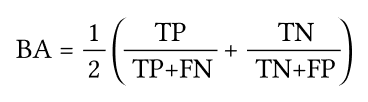
Примечание
В нашей задаче классов много (много видов номенклатуры). Но когда классов много, то расчет метрик можно свести к бинарному виду как каждый против всех (естественно, когда это возможно). И тогда можно применить расчет метрик для двух классов. Или использовать другие ухищрения применяемые в модулях для работы с метриками в Python.
Матрица путаницы — это табличное представление для описания производительности модели классификации на наборе тестовых данных, для которых известны фактические значения. Это позволяет легко идентифицировать путаницу между классами, т. е. когда один класс ошибочно помечен как другой.
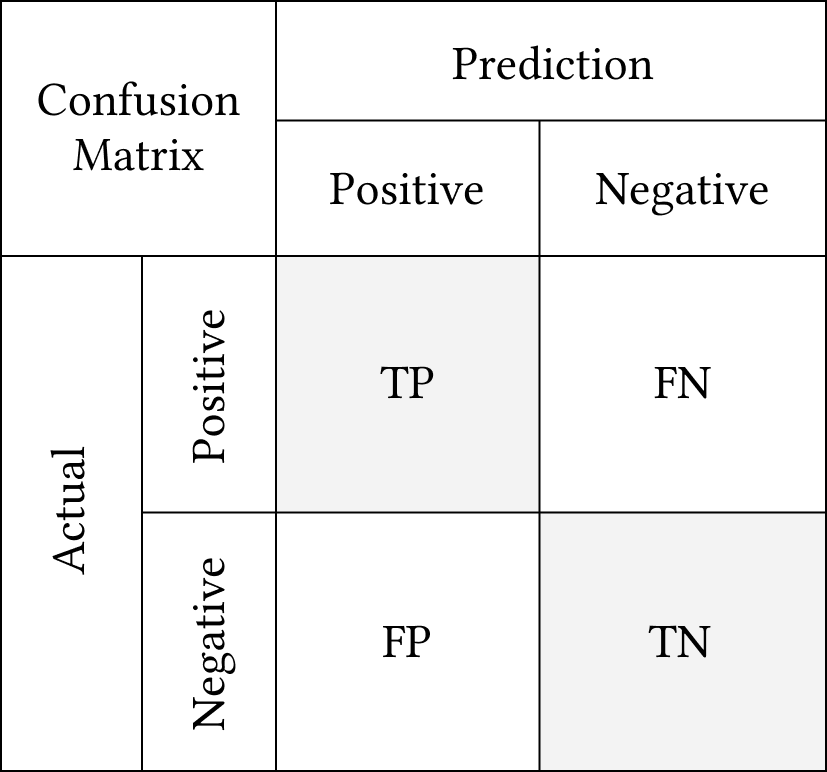
Где:
Actual — известное нам значение.
Prediction — предсказанное нам значение
Каждая ячейка в матрице путаницы говорит нам одну вещь о производительности модели.
Это:
Истинно положительные результаты (ТP) — вы предсказали положительный результат, и это правда.
Истинно отрицательные результаты (TN) — вы предсказали отрицательный результат, и это правда.
Ложноотрицательные результаты (FN) — вы предсказали отрицательный результат, но он неверен.
Ложноположительные результаты (FP) — вы предсказали положительный результат, но он неверен.
| Метрики до обучения модели | Метрики после обучения модели | Семплов | |||||||||
| № | Класс | f1 | precision | recall | balanced_accuracy | f1 | precision | recall | balanced_accuracy | test | train |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Алюминий | 0.99 | 1.0 | 0.98 | 0.98 | 1.0 | 1.0 | 1.0 | 1.0 | 97 | 386 |
| 1 | Базальт | 0.67 | 1.0 | 0.5 | 0.5 | 1.0 | 1.0 | 1.0 | 1.0 | 2 | 3 |
| 2 | Бронза | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 2 | 4 |
| 3 | БРО | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1 | 1 |
| 4 | БрХ | 0.97 | 1.0 | 0.94 | 0.94 | 1.0 | 1.0 | 1.0 | 1.0 | 1 | 3 |
| 5 | Латунь | 0.95 | 1.0 | 0.91 | 0.91 | 1.0 | 1.0 | 1.0 | 1.0 | 18 | 70 |
| 6 | Медь | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 1.0 | 1.0 | 1.0 | 11 | 43 |
| 7 | Лист нержавеющая | 0.99 | 1.0 | 0.98 | 0.98 | 1.0 | 1.0 | 1.0 | 1.0 | 1 | 3 |
| 8 | Сталь нержавеющая | 0.98 | 1.0 | 0.95 | 0.95 | 1.0 | 1.0 | 0.99 | 0.99 | 181 | 723 |
| 9 | Сталь оцинкованная | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 44 | 171 |
| 10 | Паронит | 0.99 | 1.0 | 0.97 | 0.97 | 1.0 | 1.0 | 1.0 | 1.0 | 7 | 24 |
| 11 | Сталь | 0.89 | 1.0 | 0.8 | 0.8 | 1.0 | 1.0 | 1.0 | 1.0 | 113 | 448 |
| 12 | Стеклотекстолит | 0.75 | 1.0 | 0.6 | 0.6 | 1.0 | 1.0 | 1.0 | 1.0 | 5 | 17 |
| 13 | ТМКЩ | 0.86 | 1.0 | 0.75 | 0.75 | 0.89 | 1.0 | 0.8 | 0.8 | 5 | 16 |
| 14 | Титан | 0.92 | 1.0 | 0.86 | 0.86 | 1.0 | 1.0 | 1.0 | 1.0 | 12 | 43 |
| 15 | Труба | 0.83 | 1.0 | 0.71 | 0.71 | 1.0 | 1.0 | 1.0 | 1.0 | 7 | 25 |
| 16 | Уголок сталь | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 7 | 25 |
| 17 | Фторопласт | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 2 | 4 |
Жирным курсивом выделены те строки, величины метрик по которым увеличились после обучения модели.
Количество train + test по классам может быть меньше, чем общее количество сэмплов для класса в обучающей выборке, т. к. производилась операция удаления дублей строк для каждого класса. Удаление дублей производилось простым сравнением строк. Если строки равны, то удалялась вторая и последующие строки. Также не лишним будет произвести анализ внутри классового распределения:
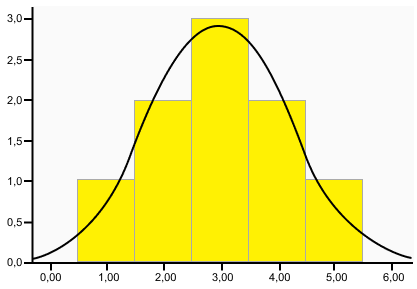
Где по вертикали откладывается количество элементов в столбике, а по горизонтали номер столбика. Если данные в классе похожи друг на друга, то график будет выглядеть примерно как на рисунке. Т. е. иметь вид нормального распределения. И наши данные будут подчиняться правилу трех сигм:
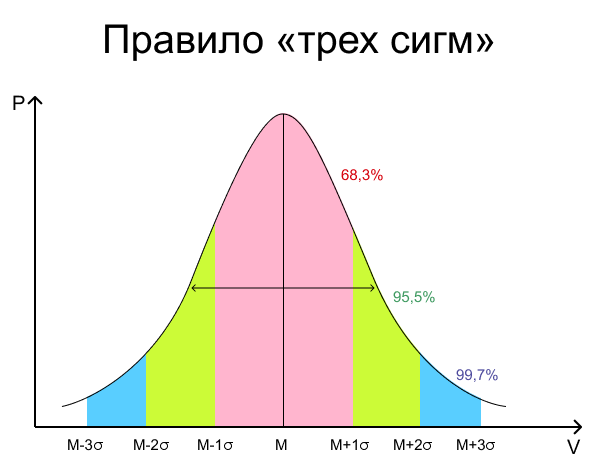
Т. е. более 99% всех данных будут лежать в пределе 3 сигм слева и справа от математического ожидания.
Мы можем легко перейти от гистограммного представления к вероятностному распределению просто поделив количество элементов в каждом столбике на количество элементов в классе.
Математическое ожидание — это среднее значение случайной величины. Обозначается как μ.
Стандартное или среднеквадратичное отклонение — это наиболее частый показатель рассеивания значений величины относительно математического ожидания. Обозначается символом σ.
Если наши данные подчиняются такому распределению, то наша модель будет обучаема. Иначе лучше перейти к другим методам машинного обучения, которые не сильно требовательны к тому, чтобы данные были нормально распределены.
Программный код для нейросетевой метрической модели не будем приводить, т. к. он очень объемный.
Модель «Наивный байесовский классификатор»
Наивный байесовский классификатор — это семейство алгоритмов классификации, которые принимают одно допущение: каждый параметр классифицируемых данных рассматривается независимо от других параметров класса.
В нашей задаче, конечно это не совсем так — т. к. появление определенного биплета иногда зависит от появления другого биплета. Но на то он и наивный. :)
Примечание
Конечно, биплеты семантически связаны друг с другом. Например, после биплета с окончанием на гласную букву реже идет биплет с началом на гласную букву. И наоборот, у биплета с окончанием на согласную букву чаще следующий биплет идет с началом на согласную букву: например — предсказать — после биплета дс идет биплет ка. Но это зависит от контекста тестового сообщения.
По сути, теорема позволяет нам предсказать класс на основании набора параметров, используя вероятность. Т. е. нам просто необходимо составить частотные таблицы для каждого наименования справочника номенклатуры.
Давайте немного разберем это на примере.
Логическая блок-схема и пример
Немного повтора из первой части статьи (пример, взятый из треда Stack Overflow stackoverflow.com/questions/10059594/a-simple-explanation-of-naive-bayes-classification/20556654#20556654):
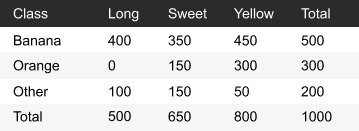
У нас есть тренировочный набор данных о 1000 фруктах.
Фрукт может быть бананом, апельсином или каким-нибудь другим (это классы).
Фрукт может быть длинным, сладким или желтым (это параметры — для нас это будут значения, счетчики гистограммы).
Из 500 бананов 400 длинные, 350 сладкие и 450 желтые.
Среди 300 апельсинов нет ни одного длинного, но оказалось 150 сладких и 300 желтых (кстати, ниже разобран метод «Взаимная энтропия» — эти два метода имеют очень похожий математический аппарат).
Из оставшихся 200 фруктов 100 оказались длинными, 150 сладкими и 50 желтыми.
Если мы получим только параметры — длину, сладость и цвет фрукта (не зная его класса), то сможем вычислить вероятность того, что фрукт окажется бананом, апельсином или чем-то другим.
Предположим, что неизвестный фрукт длинный, сладкий и желтый.
Для вычисления вероятности нужно проделать 4 простых шага:
Шаг 1: Чтобы вычислить вероятность того, что неизвестный фрукт — это банан, давайте сначала решим, похож ли этот фрукт на банан. Вот как вычисляется вероятность класса «Банан» на основании параметров «длинный», «сладкий», «желтый»:
Выглядит точно так же как уравнение, описанное выше.
Шаг 2: Начнем с числителя и подставим все значения в уравнение.
P(Long|Banana) = 400 / 500 = 0.8
P(Sweet|Banana) = 350 / 500 = 0.7
P(Yellow|Banana) = 450 / 500 = 0.9
P(Banana) = 500 / 1000 = 0.5
Перемножив значения (согласно уравнению), мы получим:
0.8 × 0.7 × 0.9 × 0.5 = 0.252
Шаг 3: Проигнорируем знаменатель, поскольку он будет одинаковым для всех последующих вычислений.
Шаг 4: Проделаем те же вычисления для других классов.
P(Orange|Long, Sweet, Yellow) = 0
P(Other|Long, Sweet, Yellow) = 0.01875
Поскольку 0,252 больше, чем 0,01875, то наивный байесовский алгоритм классифицирует этот длинный, сладкий и желтый фрукт как банан.
Этот метод требует обучения, поскольку алгоритм использует размеченный набор данных для построения таблицы.
Когда частотные таблицы уже вычислены, классификация неизвестного фрукта включает в себя только вычисления вероятностей для всех классов, а затем выбор наибольшей вероятности.
Несмотря на простоту наивный байесовский алгоритм может быть удивительно точным. Например, было установлено, что он может быть успешно применен для фильтрации спама.
Итак, как действовать мы поняли. Попробуем написать код.
Программная реализация
Благодаря уже реализованному функционалу, обучение наивного байесовского классификатора сводится к нескольким строчкам кода:
from sklearn.naive_bayes import ComplementNB # импортируем зависимости clf = ComplementNB() # создаем модель sample_weight = compute_sample_weight(class_weight='balanced', y=y) # вычисление весового вклада clf.fit(x, y, sample_weight=sample_weight) # обучение модели. Учится быстро
Отдельно стоит рассмотреть метод compute_sample_weight — датасет (в нашем случае справочник «Номенклатура») имеет для каждого вида номенклатуры (то, что наша модель должна предсказывать) разное количество элементов (записей). Если соотношение количества записей для разный видов номенклатур будет очень сильно отличаться, то модель может хорошо обучиться на тех классах (видах номенклатуры), у которых количество записей большее, т. к. записи от них будут более часто предъявляться модели при обучении. Чтобы нивелировать этот дисбаланс производится расчет относительного «веса» каждого примера.
Пример:
Допустим, нам дан список чисел: y = [1,1,1,1,0,0,1]
Здесь 5 раз встречается число 1, и два раза число 0
Производим расчет: compute_sample_weight(class_weight=’balanced’, y=y)
И получаем веса каждого примера — array([ 0.7 , 0.7 , 0.7 , 0.7 , 1.75, 1.75, 0.7 ])
Видно, что для числа 1 одинаковые весовые коэффициенты, и для числа 0 также одинаковые.
Режим "balanced"использует значения y для автоматической корректировки весов, обратно пропорциональных частотам классов во входных данных: n_samples / (n_classes × np.bincount(y))
w1 = 7/(2 × 5) = 0.7 — вес элементов 1
w0 = 7/(2 × 2) =1.75 — вес элементов 0
Видно, что вес элементов 0 выше, чем вес элементов 1. Следовательно, модель при обучении будет штрафоваться сильнее при некорректном распознавании элементов 0.
Где x — наши вектора, признаки каждого предложения, а y — истинные ответы модели, вид номенклатуры.
Время обучения на используемом датасете 2–3 секунды.
Давайте потестируем нашего байеса. :)
Результаты
Мы учили модель определять, к какому виду номенклатуры относится введенная строка:
| Тестируемое наименование (в обучающей и тестовой выборках отсутствовали) |
Вид номенклатуры истинный | Вид номенклатуры предсказанный |
|---|---|---|
| Алюминий А 1500 × 3000 мм | Алюминий | Алюминий |
| 2 × 1200 мм Алюминий | Алюминий | Алюминий |
| бокс алюм. АД31Т1 6000 | Алюминий | Алюминий |
| Базальт. картон МПБ-5 × 600 | Картон | Картон |
| картон МПБ-5 × 600 | Картон | Картон |
| картонная коробка | Картон | Картон |
| Бронза 0.8 × 600 | Бронза | Бронза |
| Бронза 0.8 × 600 — 2000мм | Бронза | Бронза |
| бронз. 0.8 × 600 + 2000 мм. | Бронза | Бронза |
| БРОФ 9 × 700 | БРОФ | БРОФ |
| брофф | БРОФ | БРОФ |
| БРО ф 6,5–0,15 0,6 × 300 | БРОФ | БРОФ |
| Круг БрХ Ø24 | КРУГ | КРУГ |
| Латунь Л63 16 × 1000 | ЛАТУНЬ | ЛАТУНЬ |
| медная пров. | МЕДЬ | МЕДЬ |
| Лист нерж. AISI 430 2B | ЛИСТ НЕРЖ. | ЛИСТ НЕРЖ. |
| нерж. сталь 304 | СТАЛЬ НЕРЖ. | СТАЛЬ НЕРЖ. |
| оцинкованная сталь 08 пс 0.55 × 1250 × 2500 мм | СТАЛЬ ОЦИНК. | СТАЛЬ ОЦИНК. |
| Паронит *1500*2000 | ПАРОНИТ | ПАРОНИТ |
| Сталь 07г 7с 8 × 100 × 190 мм | СТАЛЬ | СТАЛЬ |
| Стеклотекстолит 500 × 1500 | ТЕКСТОЛИТ | ТЕКСТОЛИТ |
| тех пластина | ТЕХПЛАСТИНА | ТЕХПЛАСТИНА |
| Титан 880 × 1130 | ТИТАН | ТИТАН |
| Труба ЛСС 80 | ТРУБА | ТРУБА |
| УГОЛОК 20 × 20 × 4 × 6000 СТ РАВНОПОЛОЧ.ОБ.ТОЧНА СТ3КП | УГОЛОК | УГОЛОК |
| Фторопласт 78 × 8900 × 510 | ФТОРОПЛАСТ | ФТОРОПЛАСТ |
Видим, что из приведенных тестов 100% распознавание вида номенклатуры для каждой тестовой строки.
Замечание: основная проблема данного метода, что если переменные сильно зависимы между собой, то модель будет работать с ошибками. Также нельзя слишком доверительно относиться к результатам выданным оператором clf.predict_proba (он возвращает «вероятности» ответов).
Но данный метод очень хорошо работает, когда можно предположить несильную корреляцию признаков — упрощенно говоря, выполняется основной базис этой математической теории, что вероятность появления каждого случайного события не зависит от вероятности появления других случайных событий.
Модель «Взаимная энтропия»
Взаимная энтропия (иначе энтропия объединения), предназначена для расчета энтропии взаимосвязанных систем (энтропии совместного появления статистически зависимых сообщений) и обозначается H(AB), где A, как всегда, характеризует передатчик, а B — приёмник.
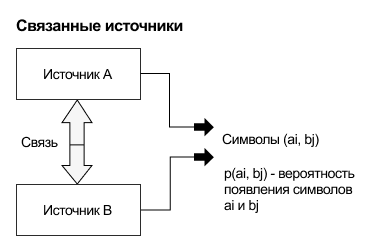
A = {a1, a2, a3, ..., an} — пространство «событий» источника;
B = {b1, b2, b3, ..., bm} — пространство «событий» приемника;
p(ai, bj) — вероятность совместного появления событий источника и приемника.
Энтропия объединения используется для вычисления энтропии совместного появления статистически зависимых сообщений.
Энтропия объединения описывает вероятность возникновение пары символов.
Взаимосвязь переданных и полученных сигналов описывается вероятностями совместных событий p(aibj), и для полного описания характеристик канала требуется только одна матрица (ее еще называют канальной матрицей объединения — от слова «канал» :) ):
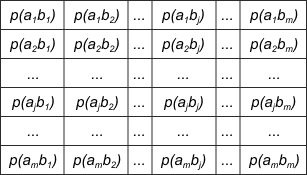
Вероятности, которые расположены по главной диагонали, определяют правильный прием, остальные — ложный. Значения цифр, заполняющих колонки или строки канальной матрицы, обычно уменьшаются по мере удаления от главной диагонали и при полном отсутствии помех все, кроме цифр, расположенных на главной диагонали, равны нулю.
Данная канальная матрица описывает влияние помех со стороны источника сообщений.
Вероятности, расположенные в одной строке таблицы, составляют полную группу событий.
Для более общего случая, когда описывается не канал, а просто взаимодействующие системы, матрица не обязательно должна быть квадратной. Очевидно, сумма всех элементов столбца с номером j даст p(bj), сумма строки с номером i есть p(ai), а сумма всех элементов матрицы равна 1. Совместная вероятность p(ai,bj) событий ai и bj вычисляется как произведение исходной и условной вероятности:
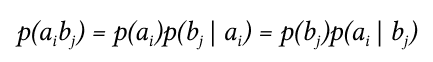
Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:
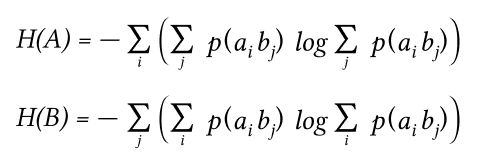
Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:
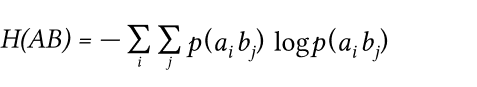
Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределенность на пару символов (у нас биплет-ы) — отправленного и полученного сообщений (у нас это гистограмма).
Совместная энтропия двух источников определяется как математическое ожидание информации всех пар событий.
Напомним, что каждая позиция в гистограмме содержит указание на то, есть конкретный биплет в тестируемом сообщении или нет.
Логическая блок-схема и пример
На вход подается предложение, которое переводим в гистограммное представление (алгоритм перевода подробно рассмотрен в первой части статьи). Также предварительно этому же действию должна быть подвергнута вся база проверки (справочник «Номенклатура» в нашем случае). Это можно сделать один раз и сохранить на диск.
Вычисляем канальную матрицу между тестируемым сообщением и проверяемым сообщением из справочника номенклатуры.
Для этого надо вычислить совместную вероятность появления символов a, b:
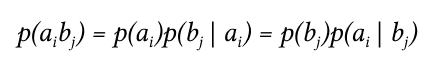
Разберем пример.
Пусть при передаче сообщений по каналу связи с шумами была получена следующая статистика:
биплет s1 из 100 раз переданных был принят как:
97 раз как s1
2 раза как s2
1 раз как s3
биплет s2 из 100 раз переданных был принят как:
98 раз как s2
2 раза как s1
биплет s3 из 100 раз переданных был принят как:
96 раз как s3
2 раза как s2
2 раза как s4
биплет s4 из 100 раз переданных был принят как:
99 раз как s4
1 раз как s3
По условию нам передали 400 биплетов.
Вероятности появления этих биплетов в передаваемых сообщениях соответственно равны:
p(s1) = 0.2475 (биплет s1 приняли 97 + 2 = 99 раз, т. е. 99/400 = 0.2475)
p(s2) = 0.255 (биплет s2 приняли 98 + 2 + 2 = 102 раз, т. е. 102/400 = 0.255)
p(s3) = 0.245 (биплет s3 приняли 96 + 1 + 1 = 98 раз, т. е. 98/400 = 0.245)
p(s4) = 0.2525 (биплет s4 приняли 99 + 2 = 101 раз, т. е. 101/400 = 0.2525)
Канальная матрица будет иметь следующий вид:
p(s1/s1) = 0.97 — условная вероятность того, что передали биплет s1, при условии получения биплета s1 (97 раз) (и / 100)
p(s1/s2) = 0.02 — условная вероятность того, что передали биплет s1, при условии получения биплета s2 (2 раза) (и / 100)
p(s1/s3) = 0.01 — условная вероятность того, что передали биплет s1, при условии получения биплета s3 (1 раз) (и / 100)
p(s1/s4) = 0.00 — условная вероятность того, что передали биплет s1, при условии получения биплета s4 (0 раз) (и / 100)
Проверка — сумма по строке должна быть = 1: 0.97 + 0.02 + 0.01 + 0.00 = 1
p(s2/s1) = 0.02 — условная вероятность того, что передали биплет s2, при условии получения биплета s1 (2 раза) (и / 100)
p(s2/s2) = 0.98 — условная вероятность того, что передали биплет s2, при условии получения биплета s2 (98 раз) (и / 100)
p(s2/s3) = 0.00 — условная вероятность того, что передали биплет s2, при условии получения биплета s3 (0 раз) (и / 100)
p(s2/s4) = 0.00 — условная вероятность того, что передали биплет s2, при условии получения биплета s4 (0 раз) (и / 100)
Проверка — сумма по строке должна быть = 1: 0.02 + 0.98 + 0.00 + 0.00 = 1
p(s3/s1) = 0.00 — условная вероятность того, что передали биплет s3, при условии получения биплета s1 (0 раз) (и / 100)
p(s3/s2) = 0.02 — условная вероятность того, что передали биплет s3, при условии получения биплета s2 (2 раза) (и / 100)
p(s3/s3) = 0.96 — условная вероятность того, что передали биплет s3, при условии получения биплета s3 (96 раз) (и / 100)
p(s3/s4) = 0.02 — условная вероятность того, что передали биплет s3, при условии получения биплета s4 (2 раза) (и / 100)
Проверка — сумма по строке должна быть = 1: 0.00 + 0.02 + 0.96 + 0.02 = 1
p(s4/s1) = 0.00 — условная вероятность того, что передали биплет s4, при условии получения биплета s1 (0 раз) (и / 100)
p(s4/s2) = 0.00 — условная вероятность того, что передали биплет s4, при условии получения биплета s2 (0 раз) (и / 100)
p(s4/s3) = 0.01 — условная вероятность того, что передали биплет s4, при условии получения биплета s3 (1 раз) (и / 100)
p(s4/s4) = 0.99 — условная вероятность того, что передали биплет s4, при условии получения биплета s4 (99 раз) (и / 100)
Проверка — сумма по строке должна быть = 1: 0.00 + 0.00 + 0.01 + 0.99 = 1
Сведем все в матрицу:
Это есть канальная матрица условных вероятностей p(a|b) — вероятность получения a, при условии получения b.
Проверка — суммы по строкам должны = 1:
p(s1|sj) = 0.97 + 0.02 + 0.01 + 0.00 = 1
p(s2|sj) = 0.02 + 0.98 + 0.00 + 0.00 = 1
p(s3|sj) = 0.00 + 0.02 + 0.96 + 0.02 = 1
p(s4|sj) = 0.00 + 0.00 + 0.01 + 0.99 = 1
Т. е. условие нормировки на 1-цу выполнено.
Произведем расчет канальной матрицы совместного появления биплетов:
p(s1, s1), p(s1, s2), p(s1, s3), p(s1, s4)
p(s2, s1), p(s2, s2), p(s2, s3), p(s2, s4)
p(s3, s1), p(s3, s2), p(s3, s3), p(s3, s4)
p(s4, s1), p(s4, s2), p(s4, s3), p(s4, s4)
Напомним формулу для расчета совместной вероятности:
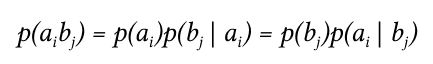
p(s1, s1) = 0.2475 × 0.97 = 0.24
p(s1, s2) = 0.2475 × 0.02 = 0.005
p(s1, s3) = 0.2475 × 0.01 = 0.002
p(s1, s4) = 0.2475 × 0.00 = 0
p(s2, s1) = 0.255 × 0.02 = 0.005
p(s2, s2) = 0.255 × 0.98 = 0.25
p(s2, s3) = 0.255 × 0.00 = 0
p(s2, s4) = 0.255 × 0.00 = 0
p(s3, s1) = 0.245 × 0.00 = 0
p(s3, s2) = 0.245 × 0.02 = 0.005
p(s3, s3) = 0.245 × 0.96 = 0.235
p(s3, s4) = 0.245 × 0.02 = 0.005
p(s4, s1) = 0.2525 × 0.00 = 0
p(s4, s2) = 0.2525 × 0.00 = 0
p(s4, s3) = 0.2525 × 0.01 = 0.003
p(s4, s4) = 0.2525 × 0.99 = 0.25
Сведем все в матрицу:
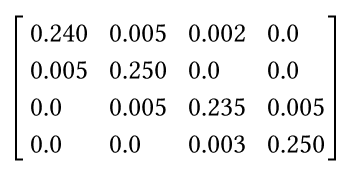
Проверка нормировки — сумма всех совместных вероятностей канальной матрицы должна быть = 1:
S = 0.24 + 0.005 + 0.002 + 0 + 0.005 + 0.250 + 0.0 + 0.0 + 0.0 + 0.005 + 0.235 + 0.005 + 0.0 + 0.0 + 0.003 + 0.25 = 1.0
Условие нормировки выполнено.
Определим энтропию объединения:
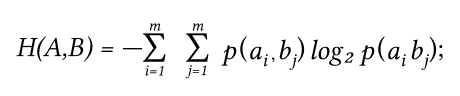
Н(А,В) = – (0.24 × log2(0.24) + 0.005 × log2(0.005) + 0.002 × log2(0.002) + 0.005 × log2(0.005) + 0.25 × log2(0.25) + 0.005 × log2(0.005) + 0.235 × log2(0.235) + 0.005 × log2(0.005) + 0.003 × log2(0.003) + 0.25 × log2(0.25)) = 2.18106 (бит на символ)
Допустим, теперь нам передали 500 биплетов. Найдем информационные потери при приеме этих 500 биплетов:
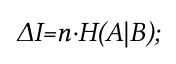
Данная формула позволяет вычислить сколько мы потеряли бит информации при приеме по зашумленному каналу:
- n = 500 при наших условиях;
- H(A|B) — условная энтропия.
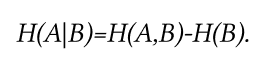
Н(А,В) — энтропия совместной системы нам уже известна.
Осталось вычислить H(B) — энтропию приемника:
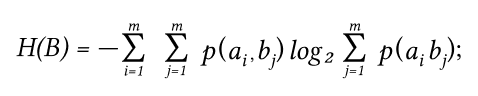
Все вероятности у нас уже есть.
Далее имеем:
Найдем информационные потери:
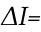500 * 0.181 = 90.5 бит Отсюда количество принятой информации будет:
Т. е. здесь мы имеем маркер: чем меньше информационных потерь (численно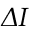 
), тем более полученный сигнал (очередная гистограмма из справочника «Номенклатура») похож на переданный сигнал (наша проверочная гистограмма, для которой мы ищем самые похожие гистограммы из справочника «Номенклатура»).
Или для нашей задачи: путем измерения 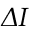между предложением проверочным и предложением из справочника «Номенклатура», тем более эти две гистограммы похожи, чем численно меньше информационные потери. Такое сравнение производим между проверочной гистограммой и всей базой «Номенклатура» и берем меньшее парное сравнение по .
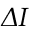Если гистограммы идентичны, то 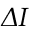= 0 — т. е. проверяемая гистограмма и гистограмма с которой проверяем идентичны.
Результаты
| Тестовое предложение (подается на вход процедуре) | Предложение, к которому отнесено оригинальное | % соответствия |
|---|---|---|
| Алюминий 1.5 × 1500 × 3000 мм | Алюминий 1.5 × 1500 × 3000 мм | 100 |
| Алюминий А5М 3 × 500 × 1500 мм | 86.97 | |
| Алюминий А5М 1,5 × 1200 × 3000 мм | Алюминий А5М 1,5 × 1200 × 3000 мм | 100 |
| Алюминий А5М 10 × 1200 × 3000 мм | 97.57 | |
| Алюминий А5Н2 1 × 1200 × 3000 мм | 91.21 | |
| Алюминий А5Н2 2 × 1320 × 2500 мм | 82.89 | |
| Сталь нерж. г/к 12Х18Н10Т 8 × 1250 × 1500 мм | Сталь нерж. г/к 12Х18Н10Т 8 × 1250 × 1500 мм | 100 |
| Сталь нерж. г/к 12Х18Н10Т 5 × 1250 × 1500 мм | 98.51 | |
| Сталь нерж. г/к 12Х18Н10Т 12 × 500 × 1500 мм | 90.81 | |
| Сталь нерж. г/к 12Х18Н10Т 4 × 1000 × 2000 мм | Сталь нерж. г/к 12Х18Н10Т 4 × 1000 × 2000 мм | 100 |
| Сталь нерж. г/к 12Х18Н10Т 20 × 480 × 1000 мм | 87.71 | |
| Сталь оцинк. 08 пс 1.5 × 1000 × 2000 мм | Сталь оцинк. 08 пс 1.5 × 1000 × 2000 мм | 100 |
| Сталь оцинк. 08 пс 1.2 × 1250 × 2500 мм | 90.98 | |
| Сталь оцинк.08 пс 0.55 × 1250 × 2500 мм | 84.2 | |
| Сталь оцинк. Zn 275 08 пс 0.7 × 1250 × 2500 мм | Сталь оцинк. Zn 275 08 пс 0.7 × 1250 × 2500 мм | 100 |
| Сталь оцинк. Zn 275 08 пс 2.5 × 1250 × 2500 мм | 95.86 | |
| Сталь оцинк. ГЛЯНЕЦ 08 пс RAL 9003 0.6 × 1250 × 2500 мм | Сталь оцинк. ГЛЯНЕЦ 08 пс RAL 9003 0.6 × 1250 × 2500 мм | 100 |
| Сталь г/к 09г2с 10 × 500 × 1000 мм | Сталь г/к 09г2с 10 × 500 × 1000 мм | 100 |
| Сталь г/к 09Г2С 5 × 1500 × 1000 мм | 89.34 | |
| Сталь г/к 09г2с 5 × 1100 × 1500 мм | 84.24 | |
| Сталь г/к 09г2с 5 × 1250 × 2500 мм | 82.13 | |
| Текстолит 2 × 1000 × 2000 мм | Текстолит 2 × 1000 × 2000 мм | 100 |
| текстолит 1 × 1000 × 2000 мм | 97.22 | |
| ВТ1-0-12 10 × 1000 × 2000 мм | ВТ1-0-12 10 × 1000 × 2000 мм | 100 |
| ВТ1-0-12 12 × 1000 × 2000 мм | 91.02 | |
| Титан ВТ1-0 10 × 1000 × 2000 мм | Титан ВТ1-0 10 × 1000 × 2000 мм | 100 |
| Титан ВТ1-0 12 × 1000 × 2000 мм | 93.46 | |
| УГОЛОК 20 × 20 × 4 × 6000 СТ ПРОКАТН.УГЛ.РАВНОПОЛОЧ.ОБ.ТОЧН СТ3КП | УГОЛОК 20 × 20 × 4 × 6000 СТ ПРОКАТН.УГЛ.РАВНОПОЛОЧ.ОБ.ТОЧН СТ3КП | 100 |
| УГОЛОК 32 × 32 × 4 × 6000 СТ ПРОКАТН.УГЛ.РАВНОПОЛОЧ.ОБ.ТОЧН СТ3КП | 97.71 |
Из приведенного списка видно, что метод достаточно близко соотносит по смыслу похожие словосочетания.
Программная реализация
Попробуем реализовать в программном коде.
Формирование данных для модели
Допустим, на вход процедуры подается предложение, для которого требуется найти близкие по написанию предложения в справочнике «Номенклатура». Также подается список предложений (из того самого справочника «Номенклатура»), среди которых процедура будет искать искомое.
Например, искомое предложение: «Алюминий А5М 1 × 1900 × 3000 мм».
Список предложений из справочника «Номенклатура»:
Предварительно можно подвергнуть каждое предложение процедуре предобработки (это описано в первой части статьи), тогда список предложений из справочника «Номенклатура»:
Т. е. процедура лемматизации произведет приведение слов в единственное число, уберет лишние значки (* ( ) - =), пробелы, также можно перевести все буквы в нижний регистр, произвести перевод слов в кириллицу и пр. Это улучшит результат работы программы.
Также нужно подвергнуть процедуре предобработки искомое предложение.
Программный код
Код функции поиска тестового предложения в базе справочника «Номенклатура» (в тексте программы даны комментарии по ходу программы):
ret = [] # создание алфавита сообщений (важно - последовательность символов должна сохраниться. set(test_query) применять нельзя!) alphabet = list({}.fromkeys(test_query).keys()) # расчет размера канальной матрицы size_vector = len(alphabet) # расчет вероятностей появления символов probabilities = {sym: test_query.count(sym) / len(test_query) for sym in alphabet} # проверка - сумма вероятностей должна == 1 assert round(np.array([value for key, value in probabilities.items()]).sum(), 4) == 1 for i, data_vector in enumerate(rows): vector = data_vector[0] if set(vector) !=set(test_query) or len(vector) != len(test_query): continue# обязательное условие что буквенный состав слов/предложений должен быть одинаковый, также и длина слов/предложений (но это условие можно снять путем ввода “внешнего” алфавита) channel_matrix = np.zeros((size_vector, size_vector), dtype=np.float) # создаем канальную матрицу # вычисление канальной матрицы условных вероятностей p(a|b) - условная вероятность события того, # что нам передали a, когда был принят b. b - событие которое произошло; a - событие которое ожидаем for index, sym_test in enumerate(test_query): channel_matrix[alphabet.index(sym_test), alphabet.index(vector[index])] += 1 # нормировка for i in range(size_vector): channel_matrix[i, ::] /= channel_matrix[i, ::].sum() assert round(channel_matrix[i, ::].sum(), 4) == 1 # проверка - сумма вероятностей по строкам должна == 1 # проверим - если матрица строго диагональная, то слова идентичны, и дальше ничего считать не надо if np.count_nonzero(channel_matrix - np.diag(np.diagonal(channel_matrix))) != 0: # произведем расчет канальной матрицы совместного появления символов по формуле p(a,b) = p(b)*p(a|b) for j in range(len(alphabet)): channel_matrix[::, j] *= np.array([p for _, p in probabilities.items()]) # проверка нормировки - сумма всех совместных вероятностей канальной матрицы должна быть = 1 assert round(channel_matrix.sum(), 4) == 1 # определим энтропию объединения по формуле H(A,B) = -SiSj[p(ai,bj)*log2(ai,bj)] (S - знак суммы) hab = [] for i in range(size_vector): hab += [channel_matrix[i, j] * math.log2(channel_matrix[i, j]) if channel_matrix[i, j] > 0 else 0 for j in range(size_vector) ] h_ab = -np.array(hab).sum() # бит на символ # проверим сколько потерялось при передаче информации - нужно найти энтропию приемника # по формуле H(B) = -SiSj[p(ai,bj)*log2(Sj[p(ai,bj)])] (S - знак суммы) hb = 0 for i in range(size_vector): log2 = math.log2(channel_matrix[i, ::].sum()) hb += np.array([channel_matrix[i, j] * log2 for j in range(size_vector)]).sum() h_b = -hb# бит/символ # расчет условной энтропии по формуле H(A|B) = H(A,B) - H(B) h_ab_if = h_ab - h_b # бит/символ # расчет информационных потерь по формуле dI = N * H(A|B) dI = size_vector * h_ab_if # бит. Если dI == 0, то потерь нет (это условие, в принципе отрабатывается при # проверке что матрица условных вероятностей является диагональной матрицей) # количество принятой информации можно посчитать так: ds = size_vector * h_b - dI # бит # коэффициент потерь (отношение условной энтропии к энтропии приемника) k = h_ab_if/h_b # (если потерь нет, то будет k == 0, иначе сравниваем с заданным коэффициентом отсечки) if k <= min_distance: ret.append((data_vector, k)) else: # матрица сразу диагональная. Точное соответствие ret.append((data_vector, 0))
Модель «Нечеткая логика»
Нечеткая логика — это форма многозначной логики, в которой истинностным значением переменных может быть любое действительное число от 0 до 1. Она используется для обработки концепции частичной истинности, где значение истинности может варьироваться от полностью истинного до полностью ложного. Напротив, в булевой логике истинностными значениями переменных могут быть только целочисленные значения 0 или 1.
Теоретическое обоснование применимости данного метода вместе с примером рассмотрено в первой части статьи.
Прежде, чем нечеткий подход к моделированию сложных систем получил признание во всем мире, прошло не одно десятилетие с момента зарождения теории нечетких множеств. И на этом пути развития нечетких систем принято выделять три периода.
Первый период (конец 60-х — начало 70-х годов) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман).
Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением).
Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.
Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem).
Также данный метод успешно можно применить и для поиска похожих слов/предложений в некоторой базе данных, например, в справочнике «Номенклатура».
Для начала давайте посмотрим на логическую блок-схему данного метода.
На входе мы имеем тестовое предложение, а также список предложений (каждый с определенным видом номенклатуры), и мы хотим предсказать вид номенклатуры для тестового предложения.
Т. е. наш метод должен выдать нам к какому виду номенклатуры относится наше тестовое предложение.
Мы также производим предобработки предложений и строим гистограммы для каждого предложения. В итоге у нас будет одна гистограмма для которой ищем и список гистограмм между которых ищем (база обучения).
Если обозначим через N длину гистограмм (для всех предложений она будет одинаковая), то каждая гистограмма будет выглядеть следующим образом:
Где xi — это количество определенных биплетов в гистограмме.
Также для каждой гистограммы у нас будет признак «Вид номенклатуры», обозначающий к какому виду номенклатуры относится данное предложение. Обозначим его через d.
Тогда для всего справочника «Номенклатура» мы можем построить матрицу:
x02 x12 x22 x32, …, xN2 | d2
x03 x13 x23 x33, …, xN3 | d3
……………
x0M x1M x2M x3M, …, xNM | dM
Где M — количество предложений в нашем справочнике «Номенклатура».
Фактически, мы получили матрицу состоящую из признаков xij — количество биплетов для каждого предложения.
Для каждого столбца x01, x02, x03, ..., x0M мы можем вычислить минимальное x0 min и максимальное x0 max значения.
Также и для столбца x11, x12, x13, ..., x1M мы можем вычислить минимальное x1 min и максимальное x1 max значения.
Также и для признаков вычислим d1 min и d1 max.
Далее применяя математический аппарат нечеткой логики (описан в первой части статьи) мы можем обучить модель и использовать ее для предсказания вида номенклатуры тестового предложения.
Блок-схема
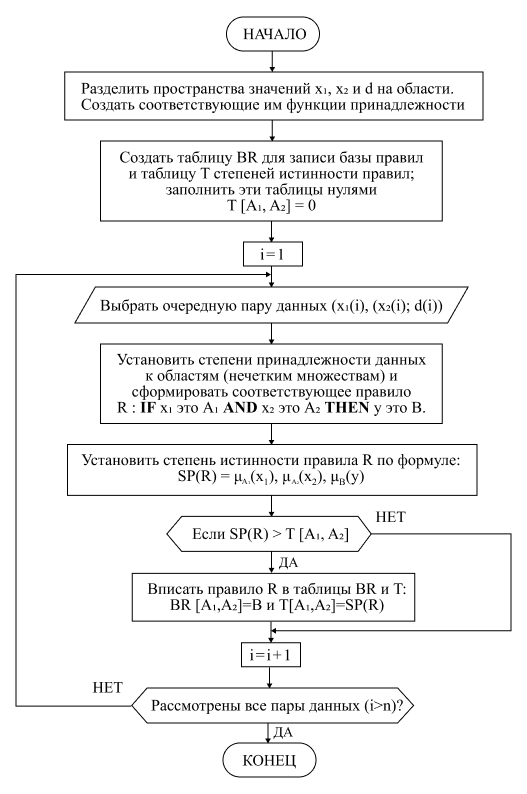
Результаты
| Тестируемое наименование (в обучающей и тестовой выборках отсутствовали) | Вид номенклатуры истинный | Вид номенклатуры предсказанный |
|---|---|---|
| Алюминий А 1500×3000 мм | Алюминий | Алюминий |
| 2×1200 мм Алюминий | Алюминий | Алюминий |
| бокс алюм. АД31Т1 6000 | Алюминий | Алюминий |
| Базальт. картон МПБ-5×600 | Картон | Картон |
| картон МПБ-5×600 | Картон | Картон |
| картонная коробка | Картон | Латунь |
| Бронза 0.8×600 | Бронза | Бронза |
| Бронза 0.8×600-2000мм | Бронза | Бронза |
| бронз. 0.8×600+2000 мм. | Бронза | Бронза |
| БРОФ 9×700 | БРОФ | БРОФ |
| брофф | БРОФ | МЕДЬ |
| БРО ф 6,5-0,15 0,6×300 | БРОФ | БРОФ |
| Круг БрХ Ø24 | КРУГ | КРУГ |
| Латунь Л63 16×1000 | ЛАТУНЬ | ЛАТУНЬ |
| медная пров. | МЕДЬ | МЕДЬ |
| Лист нерж. AISI 430 2B | ЛИСТ НЕРЖ. | СТАЛЬ НЕРЖ. |
| нерж. сталь 304 | СТАЛЬ НЕРЖ. | СТАЛЬ НЕРЖ. |
| оцинкованная сталь 08пс 0.55×1250×2500 мм | СТАЛЬ ОЦИНК. | СТАЛЬ ОЦИНК. |
| Паронит *1500*2000 | ПАРОНИТ | СТАЛЬ ОЦИНК. |
| Сталь 07г7с 8×100×190 мм | СТАЛЬ | СТАЛЬ |
| Стеклотекстолит 500×1500 | ТЕКСТОЛИТ | ТЕКСТОЛИТ |
| тех пластина | ТЕХПЛАСТИНА | ТЕХПЛАСТИНА |
| Титан 880×1130 | ТИТАН | ТИТАН |
| Труба ЛСС 80 | ТРУБА | ТРУБА |
| УГОЛОК 20×20×4х6000 СТ РАВНОПОЛОЧ.ОБ.ТОЧНА СТ3КП | УГОЛОК | УГОЛОК |
| Фторопласт 78×8900×510 | ФТОРОПЛАСТ | ФТОРОПЛАСТ |
Видим, что из приведенных тестов распознавания вида номенклатуры для каждой тестовой строки ошибка только по 4 позициям из 26.
Результаты можно качественно улучшить, если оптимизировать главный гипер-параметр модели — количество N — точек разбиения интервала для треугольной функции активации. В приведенном анализе была использована простая треугольная функция разбиения состоящая из трех треугольных функций.
Программная реализация
Обучение модели
На вход модели подаются обучающие пары {xi, yi}, где xi — числовой вектор признаков (каждый xi элемент) — это количество биплетов в предложении, а yi — это номер вида номенклатуры предложения.
Нам необходимо построить модель такую, что f:xj → y_pred
Где xj — проверочный вектор предложения (не участвующий в обучении модели), а y_pred — предсказанный моделью вид номенклатуры предложения.
Сначала находим минимальное и максимальное значения для каждого xi:
m = np.zeros((2, len(x[0])), dtype=np.int) m[0,:] = np.max(x) for i in range(m.shape[1]): for v in x: m[0, i] = min(m[0, i], v[i]) m[1, i] = max(m[1, i], v[i])
Создаем массив-следствий. Т. к. для биплетного представления при не очень длинных предложениях (до 100 символов в предложении) максимальное количество биплетов не будет более 7 (для разных xi будут разные min и max), то применяем простой режим разбиения интервала для треугольной функции:
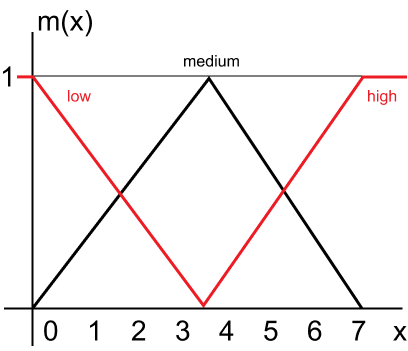
# создаем следствия y = [int(y) for y in y] interval_class_id = np.array([i for i in range(min(y), max(y) + 1, 1)]) consequent = {} for i, index_class_id in enumerate(interval_class_id): if i == 0: abc = [index_class_id, index_class_id, interval_class_id[i+1]] elif i == len(interval_class_id) - 1: abc = [interval_class_id[i-1], index_class_id, index_class_id] else: abc = [interval_class_id[i-1], index_class_id, interval_class_id[i+1]] consequent[index_class_id] = abc
Создаем предпосылки:
# создаем предпосылки antecedent = [] index_use_rule = np.zeros(m.shape[1], dtype=np.bool) for i in range(m.shape[1]): min_value = m[0, i] max_value = m[1, i] if min_value == max_value: continue index_use_rule[i] = True # terminator = (max_value - min_value) / 2 interval_x = np.arange(min_value, max_value + 1, 1) # low = [min_value, min_value, terminator] medium = [min_value, terminator, max_value] high = [terminator, max_value, max_value] # antecedent_x = {} antecedent_x['low'] = low antecedent_x['medium'] = medium antecedent_x['high'] = high # antecedent.append(antecedent_x)
А теперь самое интересное — создаем правила:
# создаем правила rules_fuzzy = [] for y_real, data in zip(y, x): antecedent_rule = [] sp = 1 for antecedent_x, plot in zip(antecedent, data): antecedent_low, antecedent_medium, antecedent_high = antecedent_x['low'], antecedent_x['medium'], antecedent_x['high'] mf_low = trimf(plot, antecedent_low) mf_medium = trimf(plot, antecedent_medium) mf_high = trimf(plot, antecedent_high) index_max = np.array([mf_low, mf_medium, mf_high]).argsort()[-1] if index_max == 0: antecedent_rule.append(antecedent_low) elif index max == 1: antecedent_rule.append(antecedent_medium) else: antecedent_rule.append(antecedent_high) sp *= [mf_low, mf_medium, mf_high][index_max] # приписывание каждому правилу степени истинности - это относится к правилам с одним и тем же условием, но с разными выводами. consequent_y_real = consequent[y_real] ms = trimf(y_real, consequent_y_real) index = [i for i, rule in enumerate(rules_fuzzy) if antecedent_rule == rule['antecedent_rule'] and consequent_y_real!= rule['consequent'] and sp * ms > rule['sp']] if len(index) > 0: add_rule = True for i in index: rules_fuzzy.pop(i) else: index = [i for i, rule in enumerate(rules_fuzzy) if antecedent_rule == rule['antecedent_rule'] and consequent_y_real != rule['consequent'] and sp * ms <= rule['sp']] add_rule = len(index) == 0 if add_rule: rules_fuzzy.append({'y_real': y_real, 'antecedent_rule': antecedent_rule, 'consequent': consequent_y_real, 'sp': sp * ms})
Формула для расчета треугольной функции (trimf):
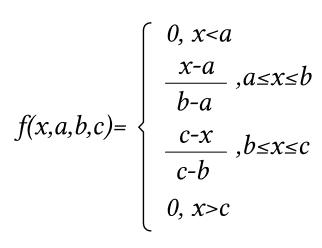
def trimf(plot, y): abc = y x = np.array([plot]) # функция расчета треугольной функции assert len(abc) == 3, a, b, c = np.r_[abc] assert a <= b and b <= c, y = np.zeros(len(x)) if a != b: idx = np.nonzero(np.logical_and(a < x, x < b))[0] y[idx] = (x[idx] - a) / float(b - a) if b != c: idx = np.nonzero(np.logical_and(b < x, x < c))[0] y[idx] = (c - x[idx]) / float(c - b) idx = np.nonzero(x == b) y[idx] = 1 return y[0]
И сохраняем созданную базу правил на диск:
if not os.path.exists('fuzzy') or not os.path.isdir('fuzzy'): os.mkdir('fuzzy') momentum = datetime.datetime.now().strftime('%Y_%m_%d_%H_%M_%S') with open(os.path.join('fuzzy', f'fuzzy_{momentum}.pkl'), 'wb') as f: BR = defaultdict(list) for v in rules_fuzzy: BR[v['y_real']].append(v['antecedent_rule']) pickle.dump([BR, index_use_rule], f) print(f'{type_model} is train and save')
Режим predict (тестируем модель)
У нас есть некоторое предложение, которое предварительно перевели в гистограмму биплетного предложения.
Мы хотим, чтобы наша модель предсказала вид номенклатуры. Для этого произведем деффузификацию по среднему центру:
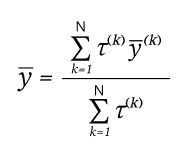
Сначала загружаем правила:
d = pickle.load(f) BR, use_rule = d[:2]
И производим расчет — на вход процедуры подается гистограммный биплетный вектор признаков (vector) предложения:
vector_predict = np.array([v for i, v in enumerate(vector) if use_rule[i]]) y = 0 assume = 0 for real, BR_rule in BR.items(): for rs in BR_rule: sk = 1 for i, r in enumerate(rs): md = trimf(vector_predict[i], r) if md == 0: md = 0.00001 sk *= md y += sk * real assume += sk predict = int(y/assume)
На этом можно и закончить математическую часть статьи, ввиду ограниченного ресурса по объему страниц к публикации. Но данная статья охватывает совсем малую часть математики, которую можно применить для такой казалось бы простой задачи, как поиск похожих слов или предложений.
И как сказал Бертран Рассел (британский математик, философ и общественный деятель): «Математика владеет не только истиной, но и высшей красотой». :)
Интеграция с 1С и наполнение базы данных
Данная математика внедрена в наше типовое решение «1С:УНФ 8. Управление предприятием общепита» (УПО). Давайте кратко рассмотрим основные моменты работы данного блока.
Следует отметить, что сейчас внедрены два метода — косинусное расстояние и нейронная метрическая модель.
Поддержка оперативных действий
В УПО настройка включения режима контроля наличия дублей номенклатуры производится следующим образом:
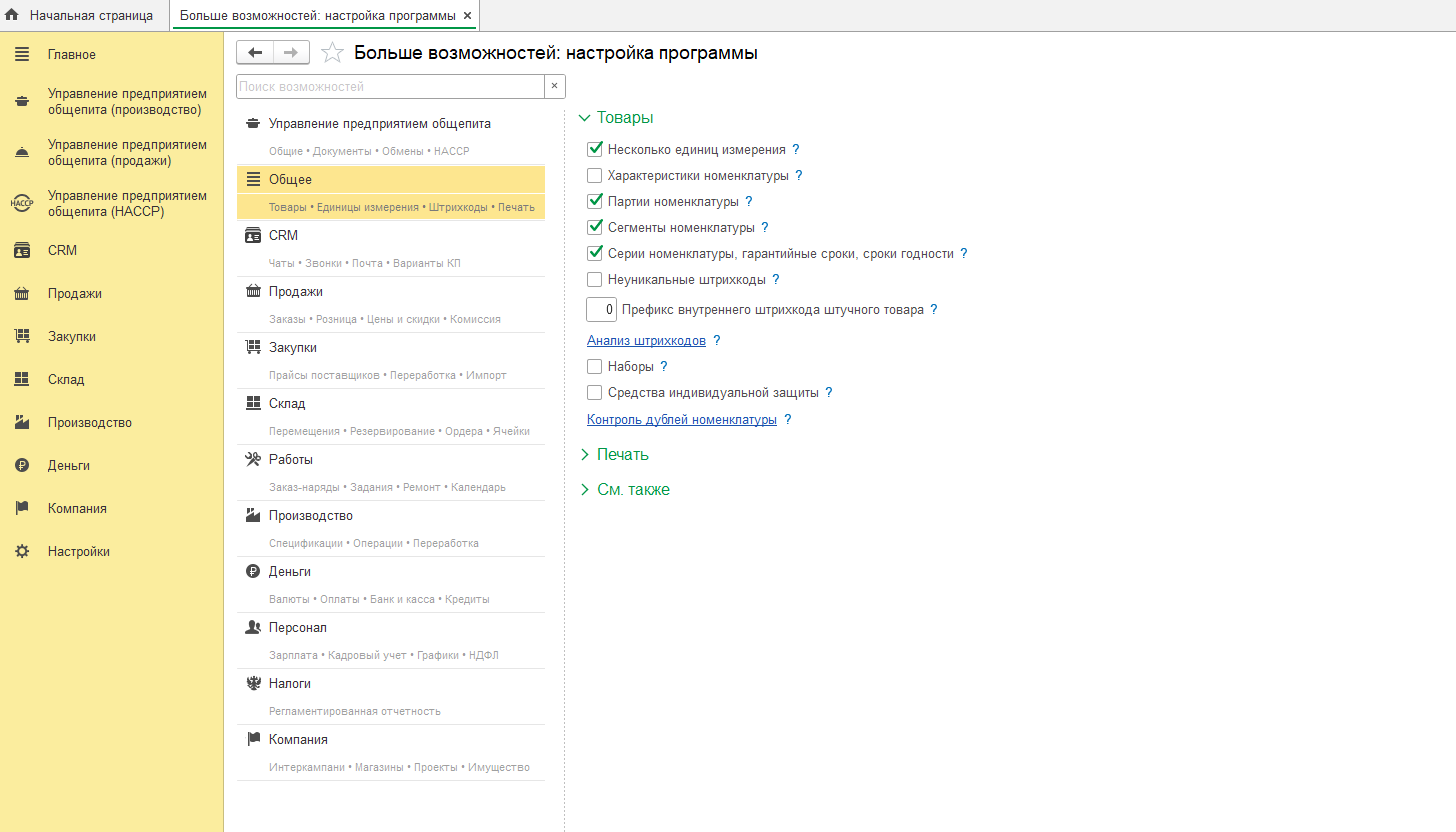
При нажатии на ссылку «Контроль дублей номенклатуры» открывается бокс настройки:
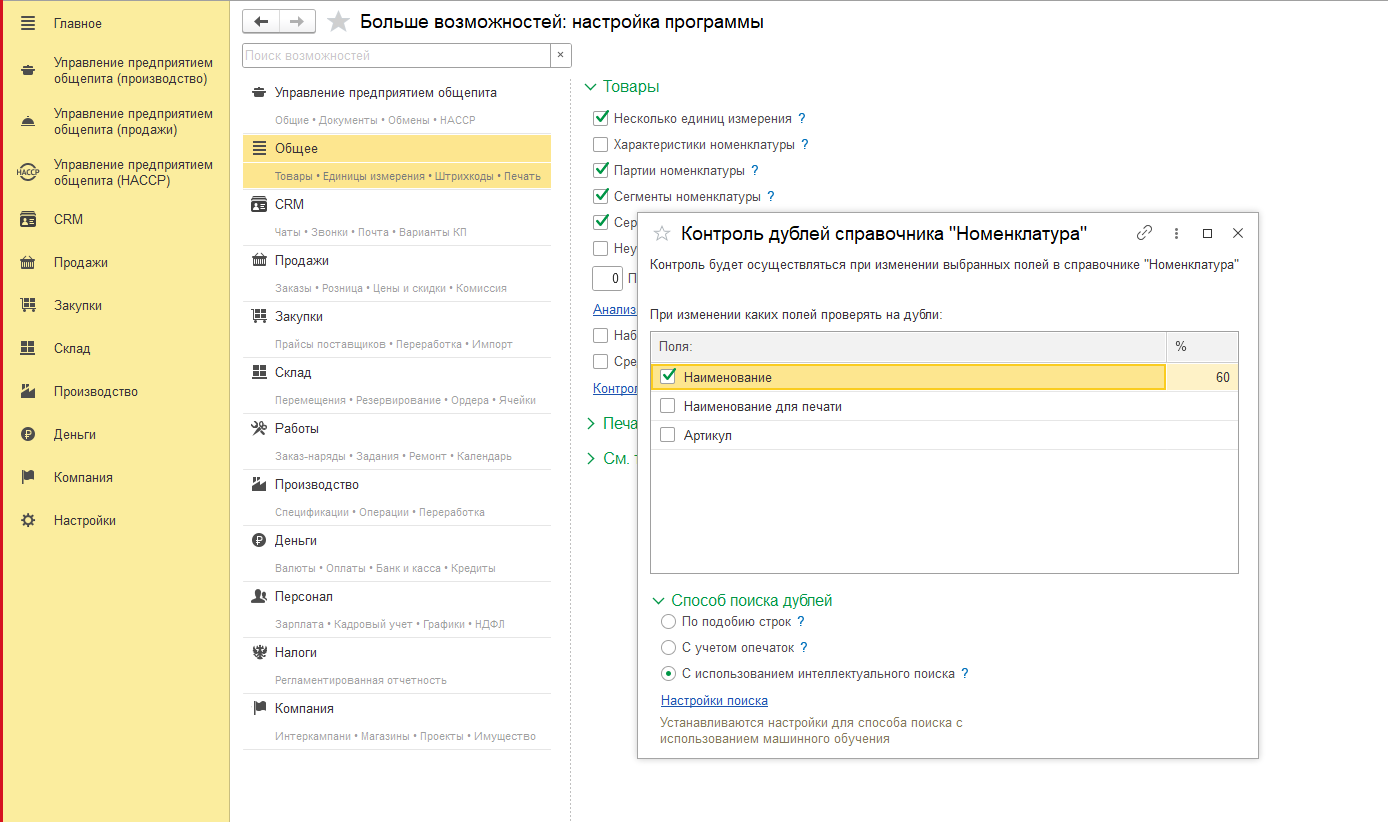
Включаем «С использованием интеллектуального поиска».
Следует отметить, что в существующем решении уже внедрен режим поиска по подобию строк (аналог типового механизма 1С) и режим «С учетом опечаток» — этот механизм использует математику Левенштейна.
Также в колонке отмеченной знаком процента задается процент похожести, выше которого при сравнении строк будет выдаваться список дублей тестируемого предложения.
Регистрация изменений справочника
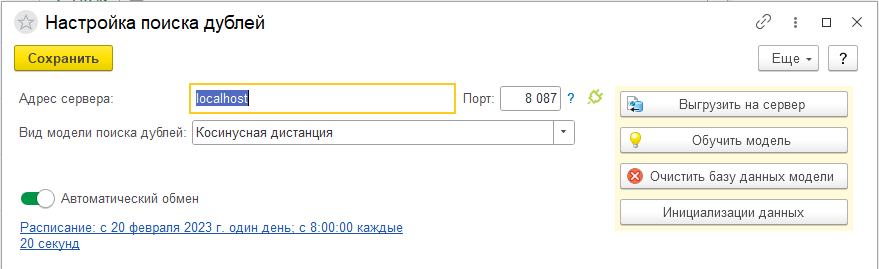
При нажатии на ссылку «Настройки поиска» открывается бокс настройки и управления.
Адрес сервера, порт — параметры подключения к серверу, обрабатывающему клиентские запросы от УПО.
Автоматический обмен — включается автоматический режим выгрузки на сторону сервера всех измененных/введенных новых строк номенклатуры.
Расписание — задается планировщик расписания, когда будет производиться выгрузка на сервер, а также обучение моделей для функционирования математики поиска дублей номенклатуры.
Также с помощью кнопок «Обучить модель», «Очистить базу данных модели», «Инициализация данных» можно производить ручное управление обучением моделей.
Вид модели поиска дублей — режим поиска на сервере дублей номенклатуры.
Использование результатов
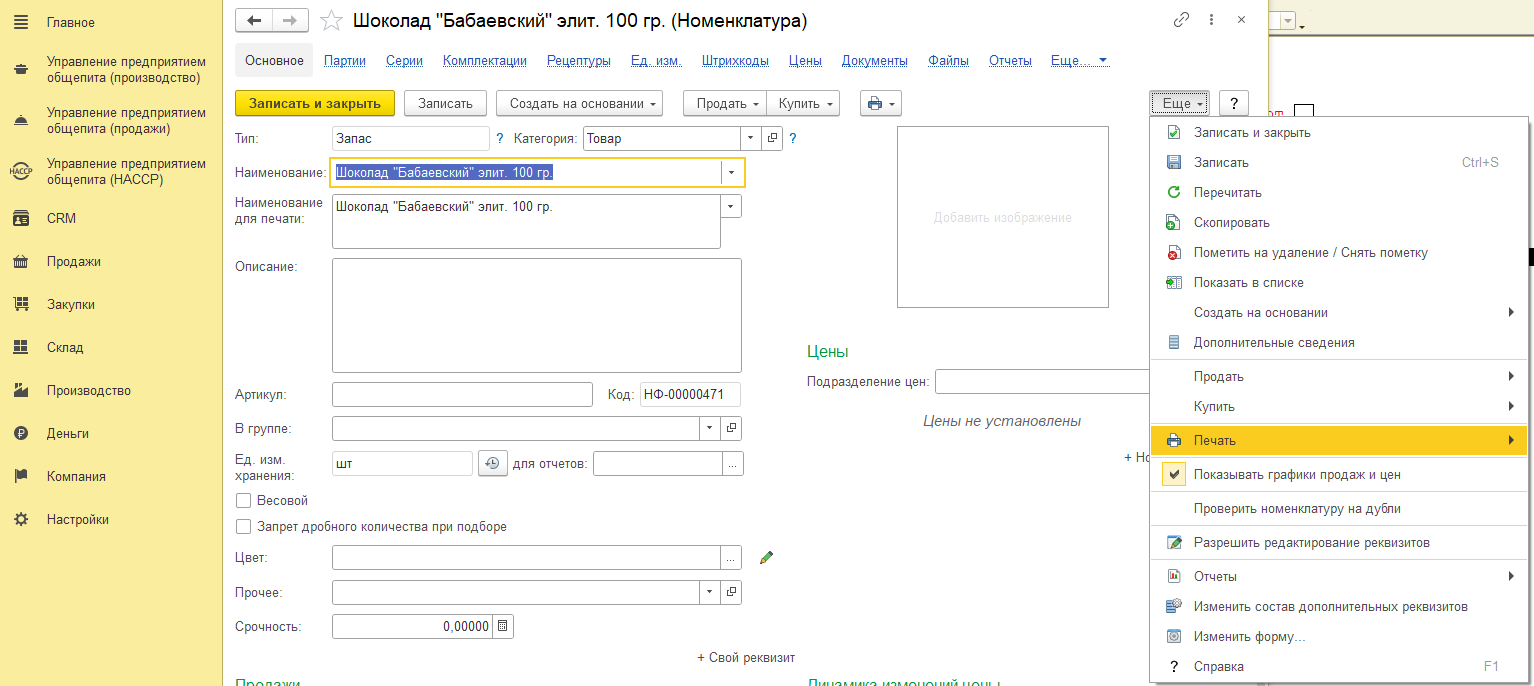
В карточке номенклатуры при нажатии на «Проверить номенклатуру на дубли» производится обращение 1С к серверной части и получение списка дублей номенклатуры, которые по мнению серверной части похожи на тестируемую строку.
Если есть строки-дубли, то выводится сообщение «Найдены дубли по наименованию», а также выводится выделенным синим «Найдены дубли по наименованию».
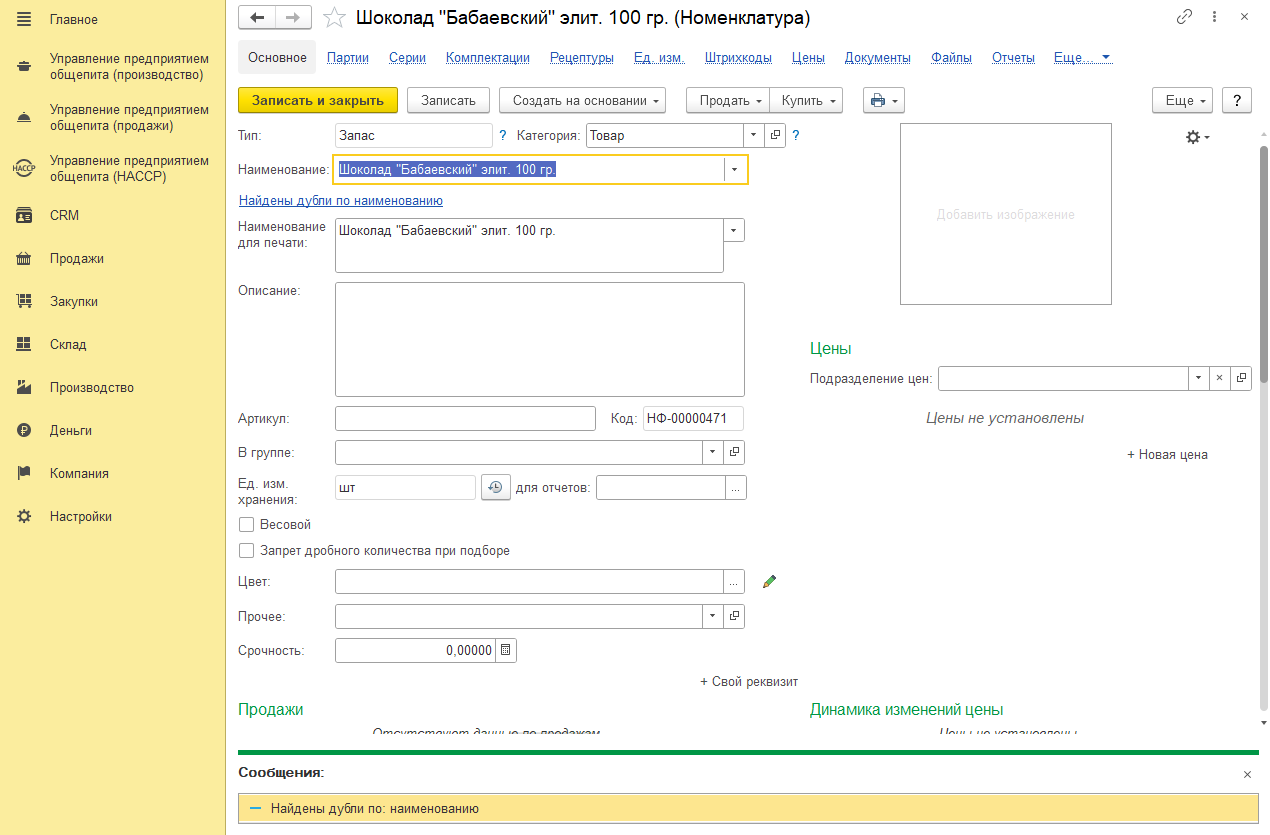
При необходимости можно просмотреть список дублей номенклатуры при активации мышью по полю «Найдены дубли по наименованию»:
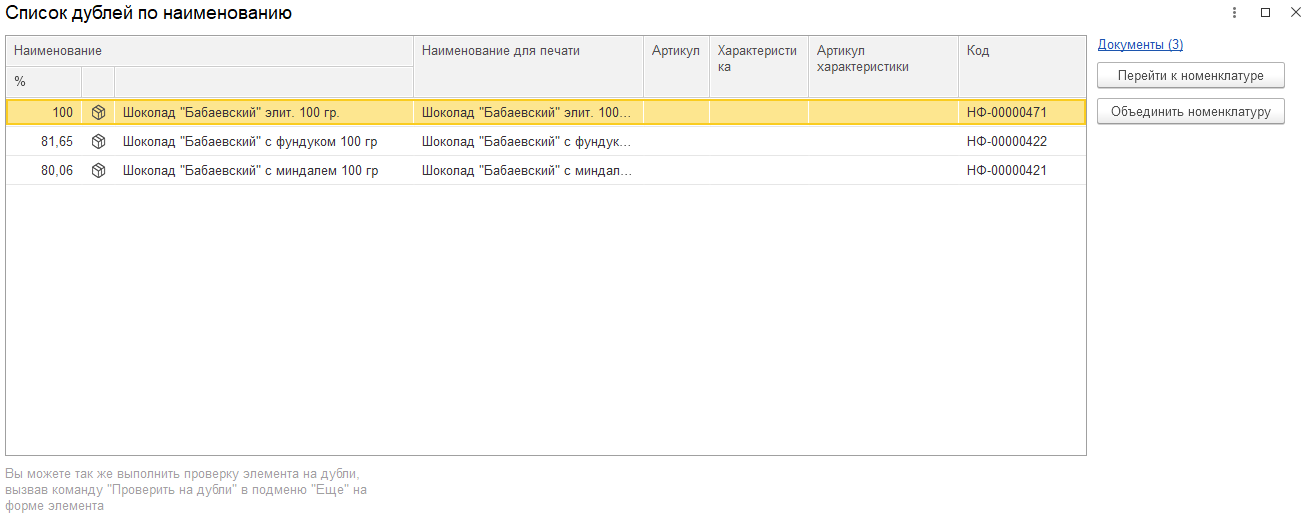
В данном примере серверная часть выдала три варианта похожих строк в порядке убывания процента схожести.
Данная математика работает и для строк введенных на английском:
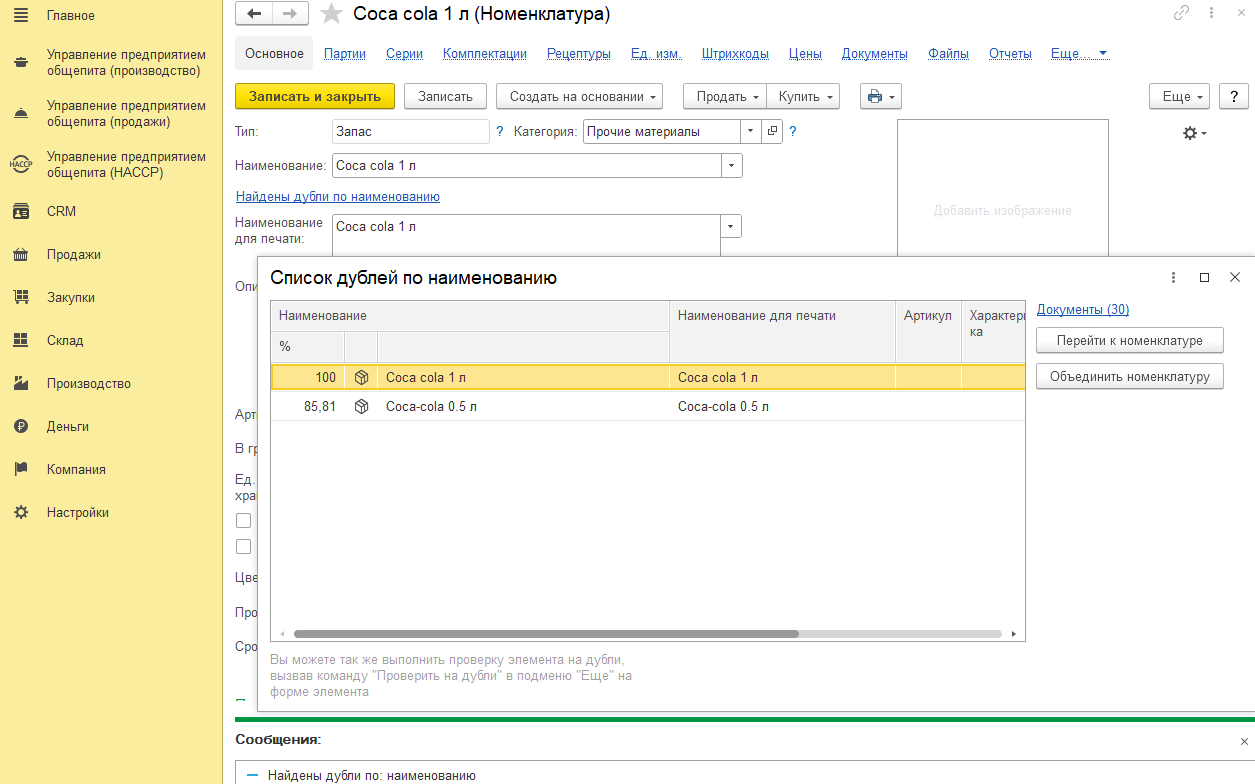
Также реализован механизм транслитерации строк. Т. е. серверная часть корректно учитывает особенность написания, например, что coca-cola и кока-кола это идентичные наименования.
Заключение
Итак, мы завершили рассказ о решении задачи поиска дублей номенклатуры. Целью повествования мы ставили показать читателю, что понятная сначала по своей формулировке задача при серьезном погружении в нее, диктует неотвратимую необходимость погрузиться в математический аппарат, чтобы разрешить коллизии похожести и непохожести, наиболее точно рассчитать лжеблизнецов и избавиться от них. Ну и конечно, чтобы вы получили наслаждение от математики, программирования и практического соприкосновения с этими науками.
От экспертов «1С-Рарус»
