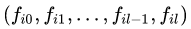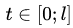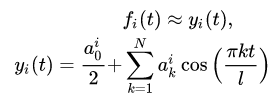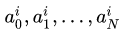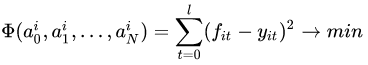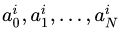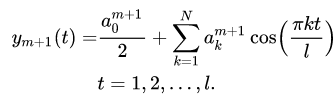Оглавление
Постановка задачи
Контрагенты организации — заказчики, покупатели. Они источник жизни для организации. Без них организация скоро зачахнет и перестанет расти и развиваться. Но не со всеми покупателями требуется работать, а только с теми, кто аккуратно выполняет свои обязательства, в том числе и по платежам. Поэтому важно иметь инструмент, который сможет ответить, на казалось бы, простой вопрос, а когда оплатит покупатель проданный ему товар или услугу и оплатит ли вообще. Вот с этой задачей попробуем разобраться.
Оценка надежности покупателя на основе бухгалтерских данных.
Итак, что нам дано.
У нас есть зачастую достаточно ограниченная информация о покупателе — это история его покупок и оплат за последние N месяцев по дням. Встает задача, зная эту информацию, сможем ли мы с некоторой долей уверенности предсказать его покупательную и платежную способность на некоторое количество дней вперед?
С первого взгляда кажется что да, если покупатель хорошо всегда платил, в срок, то и прогнозировать здесь нечего — значит и далее будет платить всегда в срок, проблем с ним у нас не будет. А вот, если покупатель немного «проблемный», но в тоже время очень статусный, отказаться от него нам бы не хотелось или состав портфеля наших покупателей на 20% состоит из таких не очень надежных покупателей, но приносящих 80% прибыли нашей организации, то отказаться от них опасно. Тут и хотелось бы иметь некоторую оценочную модель, которая нам бы сообщала о динамике оплат от этого покупателя в определенном горизонте, скажем в следующие M дней с заданной вероятностью. И чем вероятность предсказания больше, тем для нас лучше.
Обычно бухгалтеры для оценки взаиморасчетов используют оборотно-сальдовую ведомостью (ОСВ) 62 счета. А именно счет 62.01, так как на этом счете отражается финансовая деятельность по работе с покупателями в части взаиморасчетов. Дебет по этому счету содержит задолженность покупателями перед нами. Кредитовый оборот по этому счету — это чаще всего оплата от покупателя.
Вот так выглядит типичная ОСВ по 62.01 счету:
При работе с ОСВ по 62 счету можно выделить типовые корреспонденции счета 62.01:
- Продажа клиенту товаров/продукции/услуг и пр. активов:
Дб 62.01 Контрагент/Договор Кр 90.01.1 Номенклатурная группа/Ставка НДС.
Дб 62.01 Контрагент/Договор Кр 91.1 Прочие доходы. - Проведение взаимозачета:
Дб 62.02 Контрагент/Договор Кр 62.01 Контрагент/Договор. Именно поэтому выше мы говорили, что кредитовый оборот преимущественно содержит операции оплаты, но, как мы видим, не только их. - Поступление оплаты от клиента:
Дб 50 Касса Кр 62.01 Контрагент/Договор (только сумма) — наличная оплата.
Дб 51 банк. счет Кр 62.01 Контрагент/Договор (только сумма) — безнал. оплата.
Конечно существуют еще движения по счету 62.01, но в рамках нашей статьи они нам слабо интересны.
Следовательно, за выбранный период в корреспонденции со счетом 62.01 есть как дебетовые обороты, назовем их условно «Реализация», так и кредитовые обороты, назовем их условно «Оплата».
Вообще можно представить работу с покупателями следующей таблицей:
| Контрагент | Договор | СКД 62.01 | Дата | СКД 62.01 | Дата | СКД 62.01 | Дата | СКД 62.01 | Дата |
|---|---|---|---|---|---|---|---|---|---|
| Контрагент 1 | Основной №1 | 3000 | 01.01.2023 | 5000 | 05.03.2023 | 2000 | 10.03.2023 | 3000 | 18.03.2023 |
| Контрагент 1 | Основной №2 | 500 | 02.02.2023 | 600 | 23.12.2023 | 800 | 29.12.2023 | ||
| Контрагент 2 | Базовый | 8000 | 03.07.2013 | 9000 | 31.12.2013 | ||||
| Контрагент 3 | Основной | 90000 | 05.05.2022 | 100000 | 07.06.2023 | 200000 | 02.01.2024 | ||
| Контрагент 4 | Срочный | 1500 | 02.01.2023 | 2500 | 10.01.2023 | 5500 | 15.10.2023 | 6500 | 28.11.2023 |
Мы будем отслеживать именно СКД 62.01 на конец каждого дня, т. е. остаток задолженности покупателя перед нашей организацией на конец дня. Снижение этого показателя будем считать оплатой, однако в реальной жизни задача еще более сложная, так как в вышеприведенных проводках мы видели и другие причины снижения дебетового остатка.
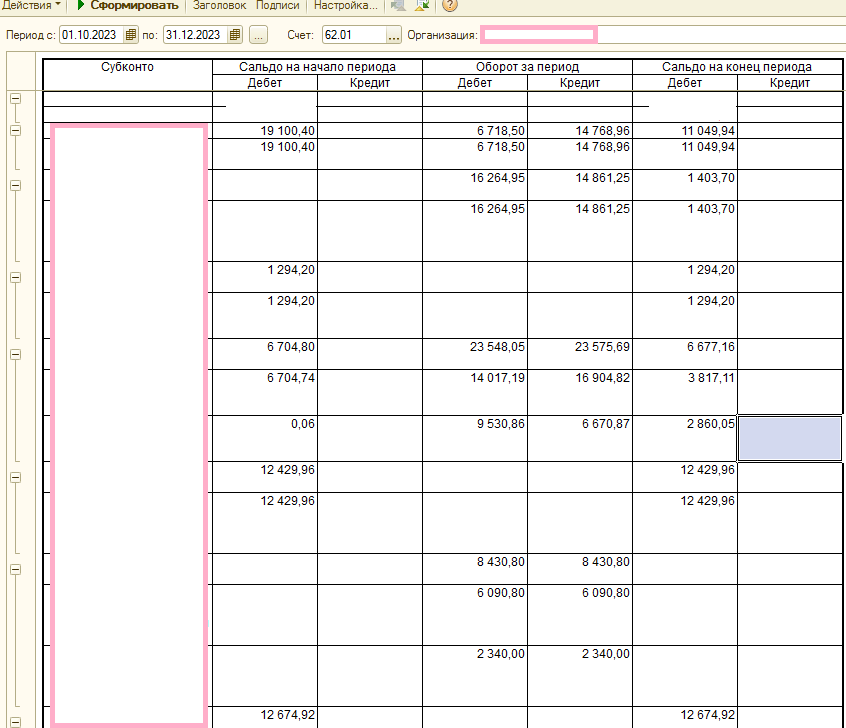
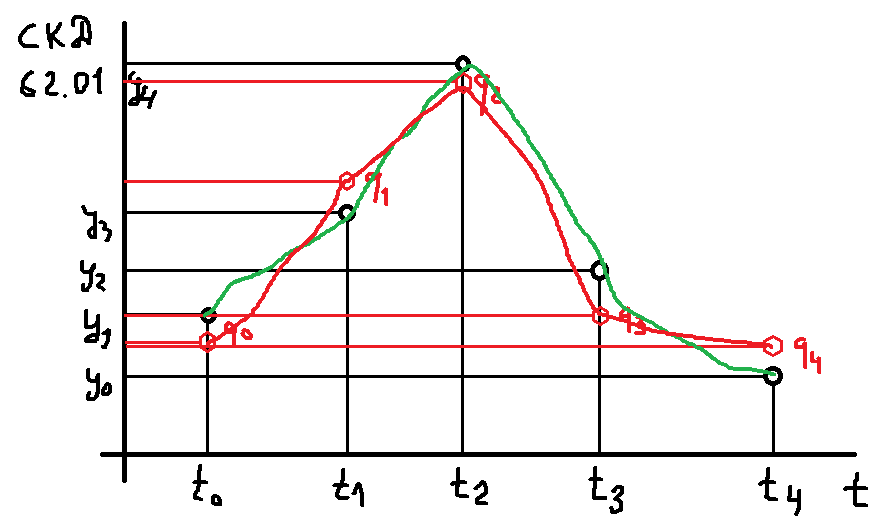
Мы можем построить динамику по 62.1 счету в декартовой системе координат:
Синими точками отмечены реализации, красными оплаты.
Из представленного графика видно, что могут быть как несколько подряд идущих реализаций, так и несколько подряд идущих оплат.
Прогнозируемая точка — дата окончательной оплаты и погашения всей задолженности, в нашем случае на графике это 10.03.2023.
То есть наша задача — это задача прогнозирования временного ряда.
Временно́й ряд
Собранный в разные моменты времени статистический материал о значении каких-либо параметров, в простейшем случае одного, исследуемого процесса. В нашем случае в качестве параметра мы договорились взять СКД 62.01 на конец каждого дня.
Слово об обобщении задачи
Кстати, далеко не обязательно исследовать только СКД 62.01 счета. Формальность математики подразумевает, что если процесс можно описать некоторой математикой, то и другой процесс, если он по заданным параметрам подходит к ранее исследуемому процессу, также можно описать точно такой же математикой и получить нужные результаты.
Входящие данные, их исследование и оценка стационарности
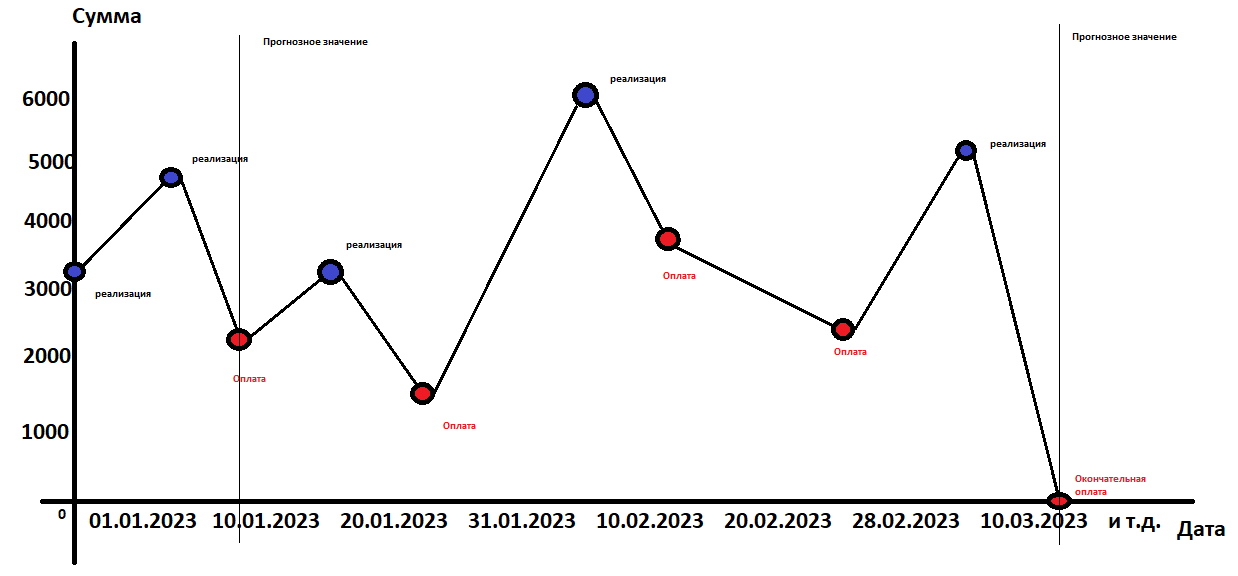
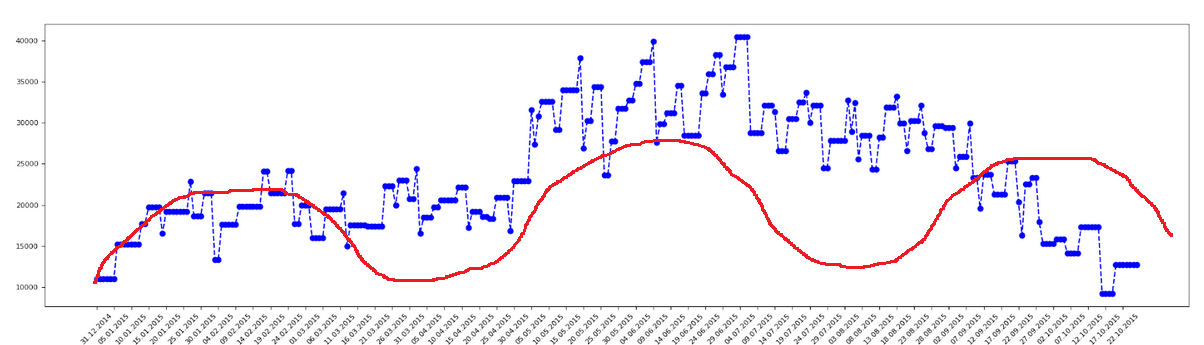
Итак, что мы имеем. У нас есть временной ряд, где по оси y откладывается уровни временного ряда, или СКД 62.01 счета на конец дня, а по оси x откладываются дни. Приведем для некоторого выбранного покупателя как может выглядеть данные по СКД 62.01 счета на каждый день, представленный в виде временного ряда.
Всегда нужно для начала посмотреть, что называется «глазами» на наши данные. Мы сразу же можем для себя предположить, что для данного временного ряда тренда скорее всего нет, есть цикличность и сезонность.
Можно сказать, что у нас задача очень сложная. Нет общего тренда, есть сезонность, есть цикличность — большие всплески.
Глаза глазами, но человек существо ленивое, и мы может просто сделали предположение, что вот такие числовые характеристики временного ряда имеют быть, чтобы ничего не считать. А хотелось бы численно оценить есть/нет тренд, какая сезонность и цикличность.
Для этого можно провести оценку стационарности.
Стационарность — это свойство временного ряда, которое означает, что такие параметры как среднее значение и стандартное отклонение уровней временного ряда не меняются со временем.
Тренд
Проведем тест на стационарность временного ряда.
Это тест на нулевую гипотезу, что временной ряд не стационарен. Т. е. мы предполагаем, что временной ряд не стационарен и пытаемся или подтвердить, или опровергнуть это предположение. Фактически производиться расчет статистических коэффициентов и их сравнение с заранее известными пределами.
p-value: 0.000315
Critical Values:
1%: −3.435
5%: −2.864
10%: −2.568
ADF Statistic — значение тестовой статистики.
Critical Values — Критические значения отсечек.
p-value — значение которое будем анализировать, сравнивая его с уровнем значимости.
ADF — статистика для стационарного ряда должна быть ниже чем любое критическое значение. У нас ADF Statistic меньше любого критического значения −4.3 против −3.4, −2.8, −2.5.
Критические значения — значения для выборок.
Тест Дики — Фуллера, это тест на единичный корень, который проверяет нулевую гипотезу о том, что α = 1 в следующем модельном уравнении:
Где:
- y (t – 1) = лаг 1 временного ряда;
- ∆ Y (t – 1) = первая разность ряда во времени (t – 1);
- et — шумовая компонента.
По сути, он имеет ту же нулевую гипотезу, что и тест единичного корня. То есть коэффициент альфа перед Y (t – 1) равен 1, что подразумевает наличие единичного корня. Если не отвергнуто, ряд считается нестационарным.
Если альфа = 1, то уравнение y (t) будет нестационарным. При альфа << 1, слагаемое y (t – 1) будет умножаться на очень малое число, и этот «довесок» не будет играть большой роли в сумме, и им можно пренебречь. А следовательно, ряд будет стационарным.
Ну а расширенный тест это то же уравнение, только с включенным регрессионным процессом более высокого порядка:
Если p-value меньше уровня значимости, обычно это 0.05, то мы можем отклонить нулевую гипотезу о нестационарности ряда и считать его стационарным. Мы получили p-value равным 0.000315, что много меньше 0.05. То есть наш ряд стационарен, и наше предположение об отсутствии тренда верно.
Сезонность
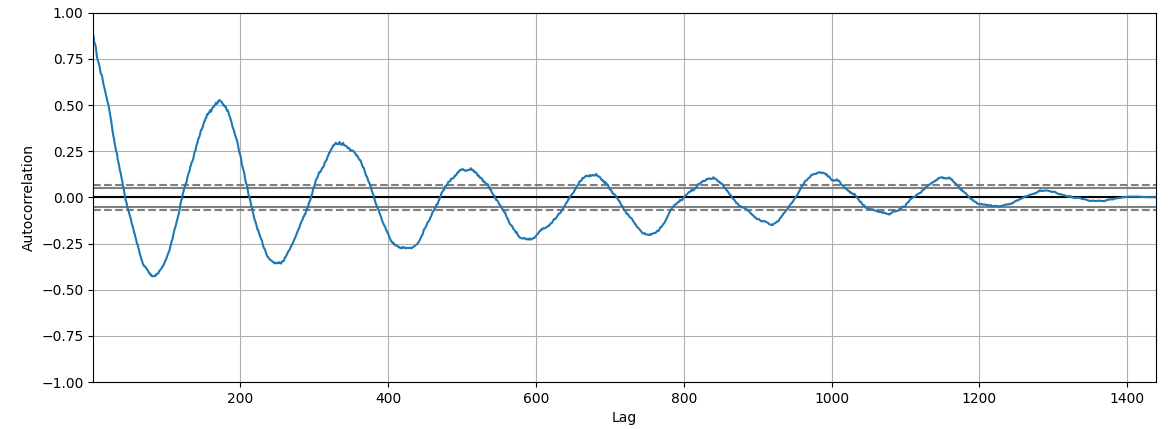
Из визуального анализа временного ряда мы можем предположить, что значения временного ряда цикличны в пределах полугода.
Если присмотреться к графику, то можно заметить, что второй «горбик» больше 0.5.
Примечание:
Первый «горбик» это корреляция исследуемой части ряда на самого себя, и естественно значение близко к единице. А это значимая корреляция числового ряда на самого себя со сдвигом, и это лаг в 180, потом в меньшей степени 320.
Наш числовой ряд имеет временной отрезок с 31.12.2014 по 12.01.2024. Количество дней 3300. 180 — это примерно полгода. То есть фактически подтверждается наше предположение о сезонности временного ряда, с примерным периодом полгода.
Корреляция значима — более 0.5, далее через лаг корреляция падает до 0.3, корреляция через два лага уже не значима, следовательно сила связи между лагами не более 2 циклов, или через каждые 6 месяцев.
Цикличность
Тут все немного сложнее.
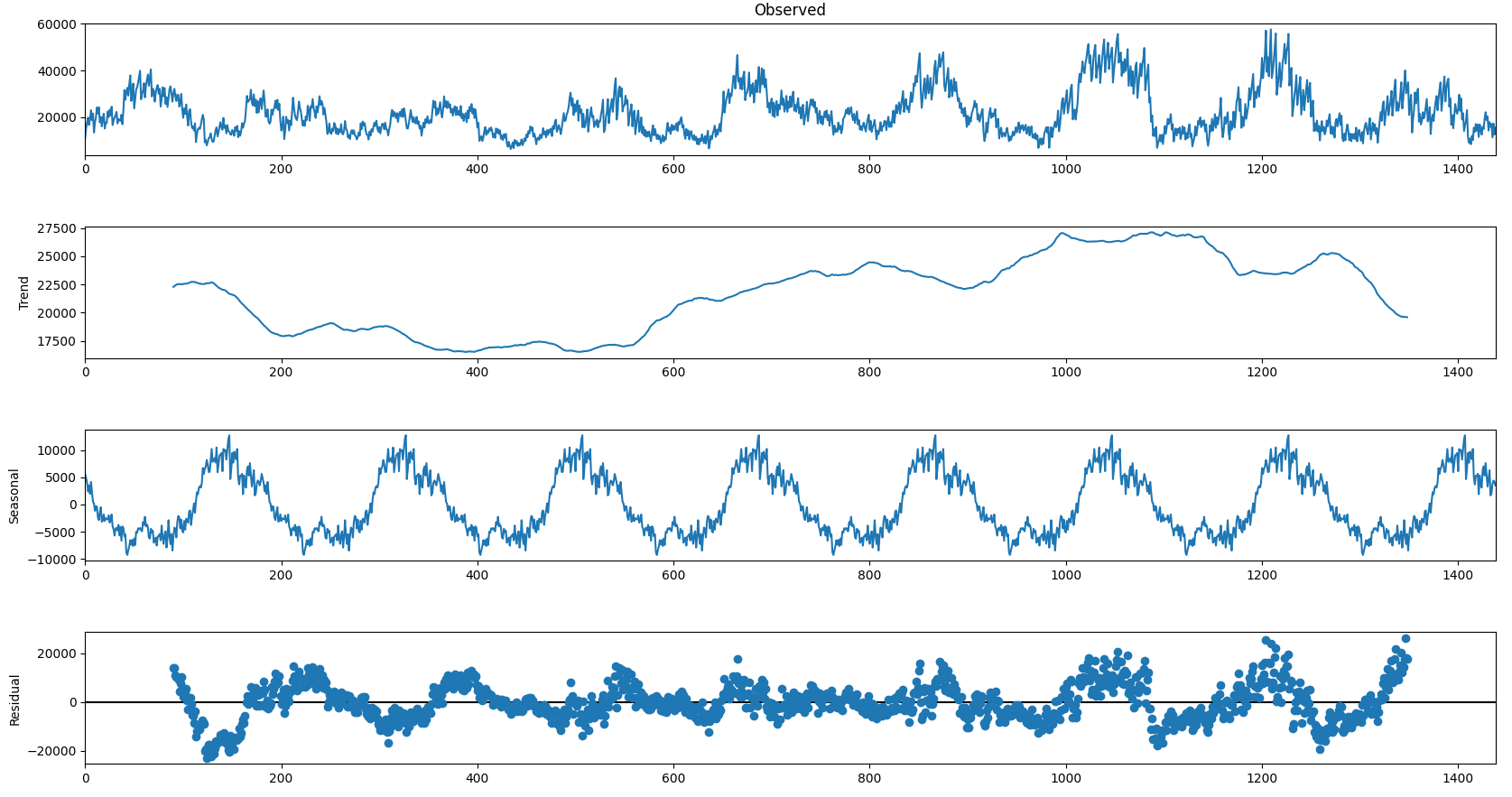
Построим графики декомпозиции числового ряда с лагом полгода.
Примечание:
Здесь необходимо небольшое отступление. На графике трендовая компонента между значениями от 600 до 1 200 возрастает. Если посмотреть на график временного ряда «Observed», это первый график на рис. 5, то можно заметить, что как раз начиная с этих же значений амплитуда временного ряда также увеличивается, а после значений 1 200 амплитуда временного ряда уменьшается, что также отражается на графике тренда.
Residual — остаток временного ряда. Т. е. это временной ряд, из которого удалены тренд и сезонность.
Сам временной ряд можно представить в виде суммы:
Y (t) = S (t) + T (t) + R (t)
S (t) — сезонный компонент.
T (t) — компонент трендового цикла.
R (t) — остаток.
Существуют несколько способов для такого разложения, но наиболее простой называется классическим разложением и заключается в том, чтобы оценить тренд.
T (t) через скользящее среднее.
S (t) как среднее без тренда.
Y (t) − T (t) для каждого сезона.
Посчитать остаток, как R (t) = Y (t) − T (t) − S (t)
Из графического анализа графика декомпозиции временного ряда можно сделать вывод о большом вкладе циклической компоненты в сумму Y (t).
Неудачные подходы к прогнозированию
В прогнозировании временных рядов, впрочем как и везде, лучше идти от простого к сложному. Зачастую простые модели дают сразу неплохой результат, на котором можно и остановиться. И к тому же простые модели зачастую легче интерпретировать.
И так, пусть у нас есть значения временного ряда y, в некоторые временные отметки t: y (t). Будем обозначать пару значений y и t как {y,t}.
Нам нужно построить такую функцию f, значения которой в некоторое t, будет иметь значение Y, как можно наиболее близкое к истинному значению y.
Невязка d = summa (Y — y)2 = summa (ft — yt)2, где суммирование идет по всем точкам нашей выборки.
Также мы возьмем не просто разницу между предсказанным и истинным значением временного ряда, а квадрат разницы, чтобы учесть в сумме положительные и отрицательные слагаемые разностей.
Невязка d должна быть как можно меньше. Тогда наша модель будет выдавать наиболее адекватные значения для каждого t, наиболее близкие к истинным значениям y:
Но не слишком близко! Иначе будет переобучение. Это целый раздел математики, который изучает следствие переобучения, а также его причины. Примем только, что наша красная линия не слишком сильно повторяет зеленую линию. То есть модуль невязки d больше нуля, но не ноль.
Вот вокруг вопроса, как выбрать функцию f, которая давала бы значение невязки наименьшее, но в тоже время минимизировать эффект переобучения, и строиться вся наука о данных. Очень сильное заявление, конечно, но в общем, так оно и есть. Можно обучить модель так, чтобы значение невязки было равно практически нулю, но толку от такой модели не будет, т. к. на данных отличающихся от данных обучения, эта модель будет выдавать совершенно необъяснимые результаты, и проще использовать модель вида «завтра будет такая же погода, как и сегодня».
Приближение синусоидой
Раз у нашего временного ряда есть ярко выраженная сезонность, то первое, что приходит в голову — давайте построим модель, в которой f будет обычная синусоида, или набор синусоид.
Например так:
Предварительно нам нужно определиться, что у нас есть t. Мы не можем просто так использовать день как «ГодМесяцДень» в расчетах, например, sin (2024.01.01). Это даже выглядит пугающе :) брррр.... Нам нужно преобразовать даты в числовые значения, чтобы компьютер смог их обрабатывать. Сделаем так, каждую временную отметку вычислим, как разницу в днях между текущим днем и первым днем в выборке.
Следовательно, ряд дней 2024.01.01, 2024.01.02, 2024.01.03... преобразуется в 0, 1, 2, ...
То есть наша невязка будет строиться так:
d = summa (a + b × sin (ωt) — y (t))2
Где:
- ω — это частота;
- b — масштабный коэффициент (амплитуда);
- a — смещение.
Суммирование делается по всем точкам временного ряда.
Это три параметра, которые надо подобрать таким образом, чтобы [a + b × sin (ωt)] была наиболее близко к y (t), или в каждой точке t, или, что лучше, в среднем по всем точкам. А еще лучше в среднем по, скажем, 30% точек из всего временного ряда. И выбирать эти 30% при каждом цикле расчетов будем случайным образом. Почему 30%? Просто так хочется. В реальности это некий гиперпараметр модели, который можно настраивать путем перебора по сетке или из каких-то интуитивных соображений.
Итак, обучение модели. Как это сделать? Какой алгоритм подбора этих волшебных a, b, ω? Тут много вариантов решения, но самый простой — это метод наименьших квадратов. Можно им. Мы используем метод градиентного спуска.
Фактически нужно взять производную от этой функции по каждому оптимизационному параметру, взять с обратным знаком, и вычислить новые значения a, b, ω на определенном экземпляре данных с неким коэффициентом скорости обучения альфа. Или сначала перебрать все примеры и потом вычислить новые a, b, ω.
- ω со штрихом — это новое, лучшее значение ω, по сравнению с ω на шаге t — 1.
- ω — это текущее значение частоты на очередном цикле.
- Альфа это скорость обучения, которая выбирается из интервала от > 0 до 1.
- d — это наша невязка, или loss-функция. Эту функцию мы и оптимизируем так, чтобы при новых параметрах a, b, ω в среднем по выборке мы получали все меньшее значение невязки на каждом следующем цикле.
В результате можно получить очень красивую картинку. Уже ради нее одной можно полдня просидеть.
Но тут нужно сделать небольшое отступление. Мы же хотели, чтобы наша модель обучалась выдавать максимально близкие значения к истинным ответам, но не настолько чтобы переобучилась. Как это сделать?
Тут поступим таким образом. Возьмем наш временной ряд и разобьем его на три части. На тренировочную, валидационную и тестовую.
На тренировочной будем подбирать параметры. На валидационной будем проверять не переобучилась ли наша модель, а на тестовом «попросим» потом нашу модель прогнозировать будущее. Наша модель фактически не будет видеть только тренировочные данные. Валидационные данные модель как бы видит косвенно, так как по ним мы выбираем из всех моделей лучшую.
Но тут нужно быть осторожным. Нужно чтобы валидационные и тренировочные данные были, как говорят, из одной генеральной совокупности.
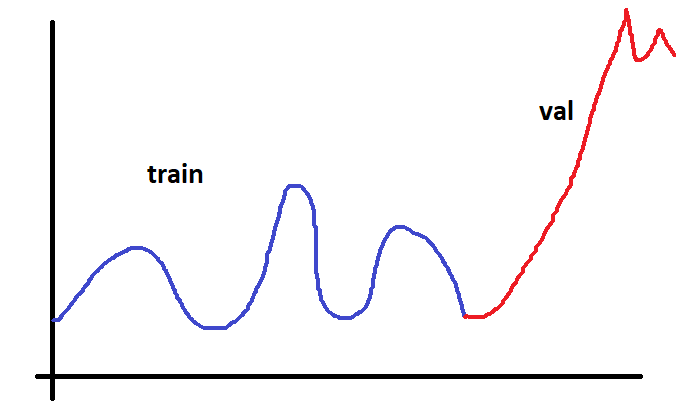
Если временной ряд будет разбит вот так:
То из этого ничего хорошего не получится. Так как обучать мы будем на данных из одного интервала, а проверять на данных совсем из другого интервала. Да и выборки не будут принадлежать к одной генеральной совокупности данных. И оценивать качество обучения нельзя по такому разбиению.
Также обязательно производим нормализацию данных с нормировкой на стандартное отклонение и нулевое среднее.
Для вычисления среднего значения просто найдем сумму всех значений выборки и поделим на ее размер.
Тут стоит привести небольшой пример, чтобы продемонстрировать положительное влияние нормировки данных.
Допустим, у нас есть таблица ненормированных данных:
| X | Y |
|---|---|
| 1000 | 20 |
| 1050 | 20 |
| 980 | 20 |
| 10000 | 30 |
| 10500 | 30 |
| 11000 | 30 |
Нам нужно построить такую модель, которая производила аппроксимацию этих табличных данных.
Первое, что нужно сделать — это построить невязку. Или выбрать вид loss-функции, которую будем минимизировать.
По определению loss = (1/N) ∑ (Fi — Yi)2
Где:
- N — количество примеров. У нас их шесть.
- ∑ — знак суммы.
- i — суммирование по i-му значению.
- Fi — предсказанное значение нашей моделью.
- Yi — истинное значение Y-ка нашей таблицы.
Нам нужно выбрать вид функции предсказания (F).
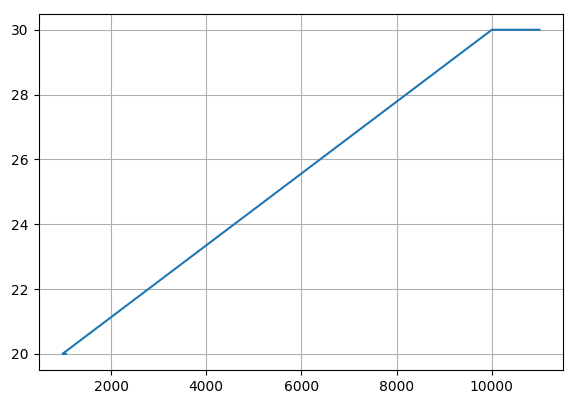
Построим график наших данных:
Из графика видно, что искомую функцию приближения следует выбрать вида F = a + b × x. Можно выбрать и другой вид, но смысла в этом особого нет, т. к. наши данные имеют линейную зависимость.
Где:
- a и b — это искомые коэффициенты прямой.
- x — это наши табличные данные, колонка X.
Итак, наша loss-функция будет иметь вид:
loss = (1/N) ∑((a + b × xi) — Yi)2
Попробуем сделать первую итерацию. Т. к. мы хотим найти такие коэффициенты a, b, что наша loss-функция будет на каждом следующем шаге итерации в среднем уменьшаться, то будем брать частные производные по a, b.
Берем производную по а:
2 × ((a + b × x) — Y) (**)
Берем производную по b:
2 × ((a + b × x) — Y) × x (***)
Примечание: примем значение коэффициента скорости обучения за 0.01.
Также слагаемое берем со знаком минус, т. к. нам нужно не увеличивать ошибку, а уменьшать, т. е. «двигаемся» в направлении антиградиента функции.
Расчет новых значений по а, b:
a (t + 1) = a (t) — 0.01 × 2 × ((a (t) + b (t) × x) — Y)
b (t + 1) = b (t) — 0.01 × 2 × ((a (t) + b (t) × x) — Y) × x
Нас интересуют слагаемые, выделенные как (**) и (***).
Допустим, начальные значения коэффициентов a, b выберем как а = 0, b = 1.
Подставляем табличные данные:
| X | Y | a (t + 1) = a (t) — 0.01 × 2 × ((a (t) + b (t) × xi) — Yi) | b (t + 1) = b (t) — 0.01 × 2 × ((a (t) + b (t) × xi) — Yi) × xi | loss = ((a (t + 1) + b (t + 1) × xi) — Yi)2 |
|---|---|---|---|---|
| 1000 | 20 | 0 — 0.01 × 2 × ((0 + 1 × 1000) — 20) = —19.6 | 1 — 0.01 × 2 × ((0 + 1 × 1000) — 20) × 1000 = —19599.00 | ((—19.6 — 19599 × 1000) — 20)2 = 384122353242368.02 |
| 1050 | 20 | 0 — 0.01 × 2 × ((0 + 1 × 1050) — 20) = —20.6 | 1 — 0.01 × 2 × ((0 + 1 × 1050) — 20) × 1050 = —21629.00 | ((—20.6 — 21629 × 1050) — 20)2 = 515766383292688.44 |
| 980 | 20 | 0 — 0.01 × 2 × ((0 + 1 × 980) — 20) = −19.2 | 1 — 0.01 × 2 × ((0 + 1 × 980) — 20) × 980 = —18815.00 | ((—19.2 — 18815 × 980) — 20)2 = 3399871103285616.60 |
| 10000 | 30 | 0 — 0.01 × 2 × ((0 + 1 × 10000) — 30) = —199.4 | 1 — 0.01 × 2 × ((0 + 1 × 10000) — 30) × 10000 = —1993999.00 | ((—199.4 — 1993999 × 10000) — 30)2 = 3.97603e+20 |
| 10500 | 30 | 0 — 0.01 × 2 × ((0 + 1 × 10500) — 30) = —209.4 | 1 — 0.01 × 2 × ((0 + 1 × 10500) — 30) × 10500 = 2198699.00 | ((—209.4 — 2198699 × 10500) — 30)2 = 5.32979e+20 |
| 11000 | 30 | 0 — 0.01 × 2 × ((0 + 1 × 11000) — 30) = —219.4 | 1 — 0.01 × 2 × ((0 + 1 × 11000) — 30) × 11000 = 2143399.00 | ((—219.4 — 2143399 × 11000) — 30)2 = 5.55893e+20 |
loss = (⅙) × (384122353242368.02 + 515766383292688.44 + 3399871103285616.60 + 3.97603e+20 + 5.32979e+20 + 5.55893e+20) = В общем ну оооочень большое число :) — порядка 10 в двадцатой.
Теперь проведем простую нормировку данных — поделим значения колонки X на максимальное значение для колонки X. Это 11000.
Также поделим значения колонки Y на максимальное значение для колонки Y. Это 30.
| X | Y | a (t + 1) = a (t) — 0.01 × 2 × ((a(t) + b(t) × xi) — Yi) | b (t + 1) = b (t) — 0.01 × 2 × ((a(t) + b(t) × xi) — Yi) × xi | loss ((a (t + 1) + b (t + 1) × xi) — Yi)2 |
|---|---|---|---|---|
| 0,090 | 0,666 | 0 — 0.01 × 2 × ((0 + 1.0 × 0.090) — 0.666) = 0.01152 | 1.0 — 0.01 × 2 × ((0 + 1.0 × 0.090) — 0.666) × 0.090 = 1.00103 | ((0.01152 + 1.00103 × 0.090) — 0.666)2 = 0.3185 |
| 0,095 | 0,666 | 0 — 0.01 × 2 × ((0 + 1.0 × 0.095) — 0.666) = 0.01142 | 1.0 — 0.01 × 2 × ((0 + 1.0 × 0.095) — 0.666) × 0.095 = 1.00108 | ((0.01142 + 1.00108 × 0.095) — 0.666)2 = 0.3130 |
| 0,089 | 0,666 | 0 — 0.01 × 2 × ((0 + 1.0 × 0.089) — 0.666) = 0.01154 | 1.0 — 0.01 × 2 × ((0 + 1.0 × 0.089) — 0.666) × 0.089 = 1.00102 | ((0.01154 + 1.00102 × 0.089) — 0.666)2 = 0.3196 |
| 0,909 | 1 | 0 — 0.01 × 2 × ((0 + 1.0 × 0.909) — 1.0) = 0.00181 | 1.0 — 0.01 × 2 × ((0 + 1.0 × 0.909) — 1.0) × 0.909 = 1.00165 | ((0.00181 + 0.00165 × 0.909) — 1.0)2 = 0.9933 |
| 0,954 | 1 | 0 — 0.01 × 2 × ((0 + 1.0 × 0.954) — 1.0) = 0.00092 | 1.0 — 0.01 × 2 × ((0 + 1.0 × 0.954) — 1.0) × 0.954 = 1.00087 | ((0.00092 + 0.00087 × 0.954) — 1.0)2 = 0.9965 |
| 1 | 1 | 0 — 0.01 × 2 × ((0 + 1.0 × 1.0) — 1.0) = 0.0 | 1.0 — 0.01 × 2 × ((0 + 1.0 × 1.0) — 1.0) × 1.0 = 1.0 | ((0.0 + 1.0 × 1.0) — 1.0)2 = 0.00 |
loss = (⅙) × (0.3185 + 0.3130 + 0.3196 + 0.9933 + 0.9965 + 0.00) = 0.49
В результате мы видим, что без нормировки ошибка на первой итерации получается порядка 10 в двадцатой, при нормализации данных ошибка на первой итерации 0.49. Здесь, конечно, надо смотреть не на порядок самой ошибки, хотя это уже само по себе заставляет задуматься, а на то, что если поверхность градиента очень сложная, то чтобы не проскочить глобальный минимум функции, который мы и ищем — это и есть наше решение, то нам для ненормированных данных придется сильно уменьшить коэффициент обучения. Для этого примера сделать альфа порядка 10 в минус 20. Тогда ошибка будет достаточно малой, но время обучения возрастает очень сильно. Что зачастую неприемлемо. В общем, данные надо нормировать, тогда коэффициент обучения можно делать достаточно большим, но < 1 конечно, чтобы время обучения было не равным количеству лет нашей жизни :).
Можно и нужно делать коэффициент обучения не постоянным на все время обучения, а переменным, что может снять много проблем.
Важно!
Надо отметить, что нормировку обязательно применять, если в данных есть не один столбец данных, а несколько, имеющих в свою очередь разные масштабы данных. Например, если есть в данных колонка, содержащая возраст человека, и колонка, содержащая заработную плату человека. Возраст человека измеряется от 0 до 120. Заработная плата может исчисляться в миллионах. Если не произвести нормировку на максимальное значение для возраста и для заработной платы, то коэффициенты модели будут больше иметь влияние от данных по заработной плате. И модель плохо «выучит» данные колонки по возрасту. В результате чего для модели будет иметь решающее значение разница между заработной платой, а не разница между возрастом, что для бизнес-логики, для которой строиться модель может быть неправильно.
Для вычисления стандартного отклонения временного ряда найдем сумму квадратов разниц между каждым значением временного ряда и средним значением временного ряда, разделим на N — 1 и возьмем корень из значения.
В итоге, каждое значение временного ряда подвергнем вычитанию среднего значения и делению на стандартное отклонение.
Также стоит заметить, что еще одним подбираемым гиперпараметром будет количество синусоид в формуле для loss-функции. И тогда наша loss-функция будет иметь вид для трех синусоид:
d = summa (a + b0 × sin (ω0t) + b1 × sin (ω1t) + b2 × sin (ω2t) — y (t))2
И оптимизировать уже будем семь параметров модели — a0, b0, b1, b2, ω0, ω1, ω2.
Итак. Модель мы обучили. Что мы имеем в результате?
Но сначала договоримся о том, как численно мы будем оценивать качество работы модели.
MAE, средняя абсолютная ошибка — это среднее значение всех абсолютных ошибок прогнозирования, где ошибкой прогнозирования является разница между фактическим значением и прогнозным значением.
Важно!
Данная оценка (MAPE) применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности — это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт. ч., a прогнозная = 10 руб/МВт. ч., тогда MAPE = (0.01 — 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт. ч. Для рядов, содержащих значения близкие к нулю, применяют оценку ошибки прогноза именно MAE.
Обучение будем производить отдельно для шести моделей. Каждая модель содержит разное количество синусоид. От одной до ста. Также будем применять поиск лучшего результата для каждой модели путем перезапуска обучения с выбором минимального значения MAE на тестовой выборке. Также проверим идею о том, что применение регуляризации может уменьшить эффект переобучения и улучшит предсказательную способность модели.
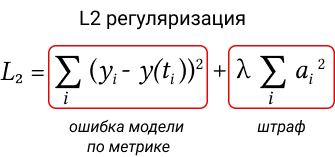
L2 регуляризация — применение регуляризации к функции потерь добавляется штраф, пропорциональный квадрату величины весов модели. Это заставляет модель не только минимизировать ошибку на обучающих данных, но и сохранять веса как можно меньшими. λ — гиперпараметр, контролирующий силу регуляризации.
Здесь под весами модели подразумевается параметры модели, которые подбираются таким образом, чтобы на каждом шаге модель выдавала в среднем более близкие значения к истинным значениям.
Есть еще L1 регуляризация. И не только.
| Количество синусоид | MAE | MAE |
MAE |
MAE |
|---|---|---|---|---|
| 1 | 3481.57 | 2544.88 | 2466.04 | 2450.43 |
| 5 | 9341.03 | 2152.89 | 2366.64 | 3019.18 |
| 10 | 4466.87 | 2472.05 | 2290.78 | 2199.50 |
| 20 | 3905.35 | 4140.41 | 2816.79 | 2567.92 |
| 50 | 5015.77 | 3433.794 | 4177.59 | 2856.71 |
| 100 | 9861.31 | 5737.36 | 5737.36 | 6357.80 |
Из приведенных замеров видно, что применение регуляризации улучшает прогнозный результат модели.
Наилучший результат получен для модели с пятью синусоидами и с коэффициентом регуляризации L2 = 0.0001.
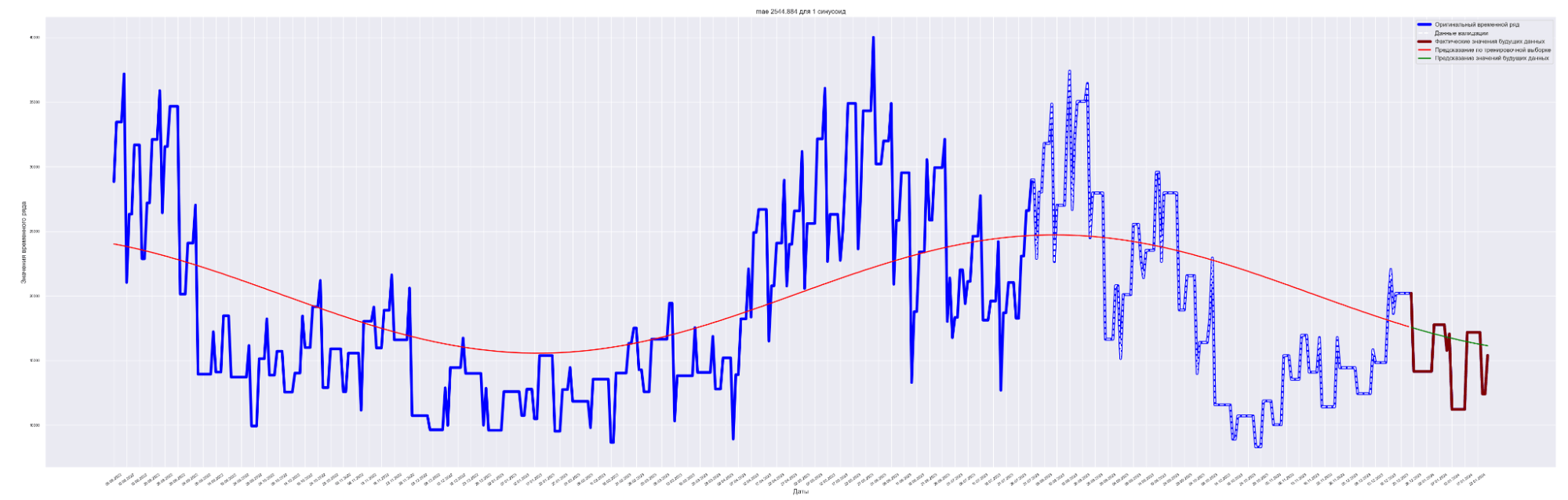
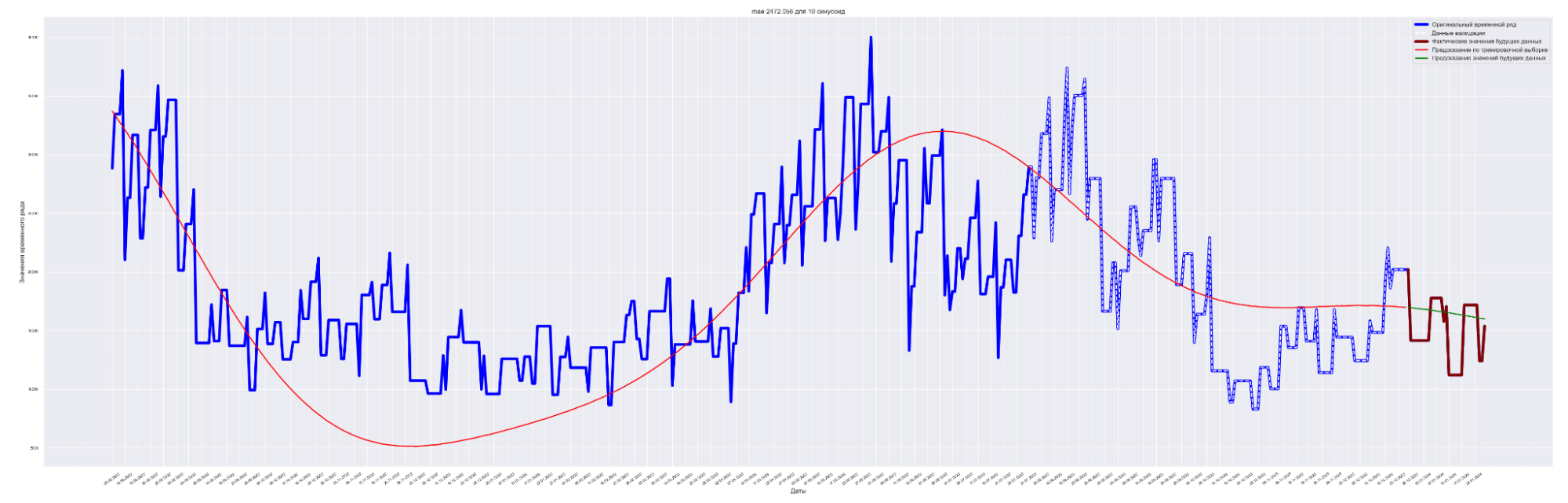
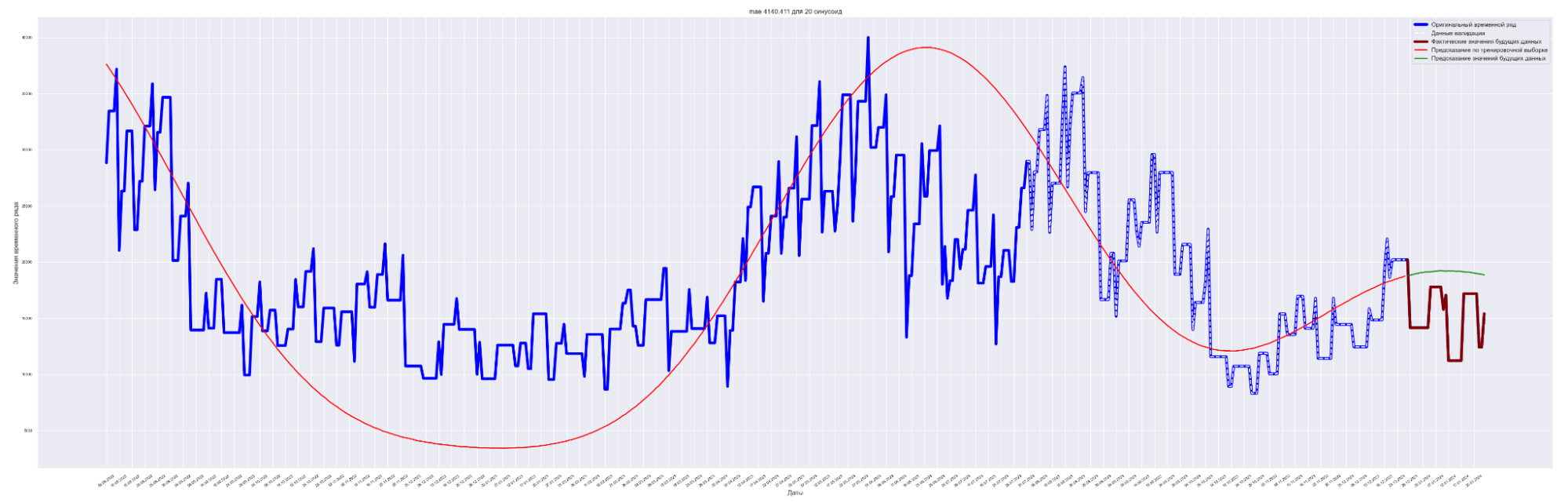
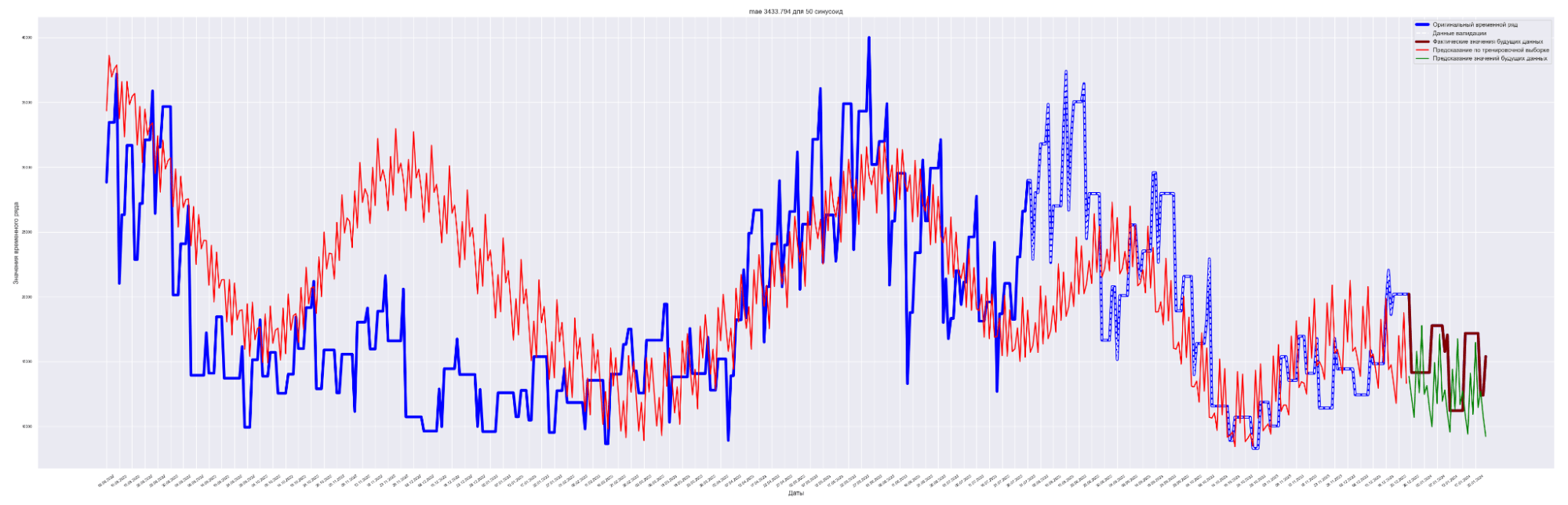
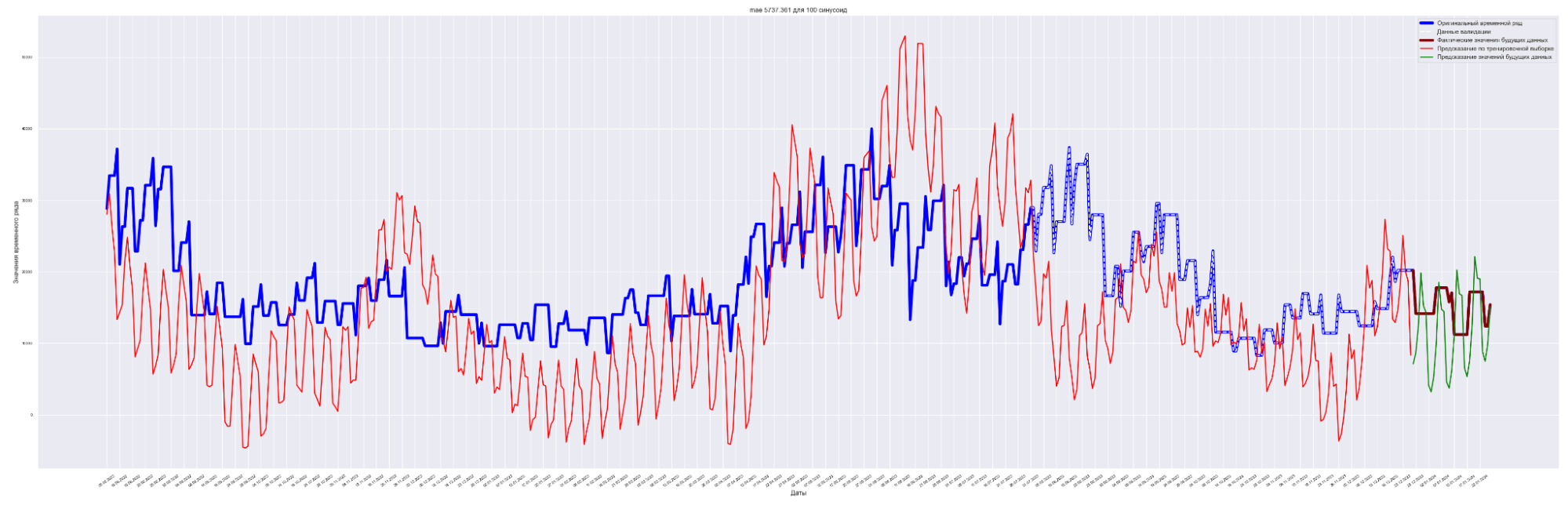
Посмотрим графики — наложение прогнозного значения на сам временной ряд.
Для вывода используем данные с коэффициентом регуляризации = 0.0001.
А почему так? Почему с ростом количества синусоид предсказательное качество нашей модели ухудшается?
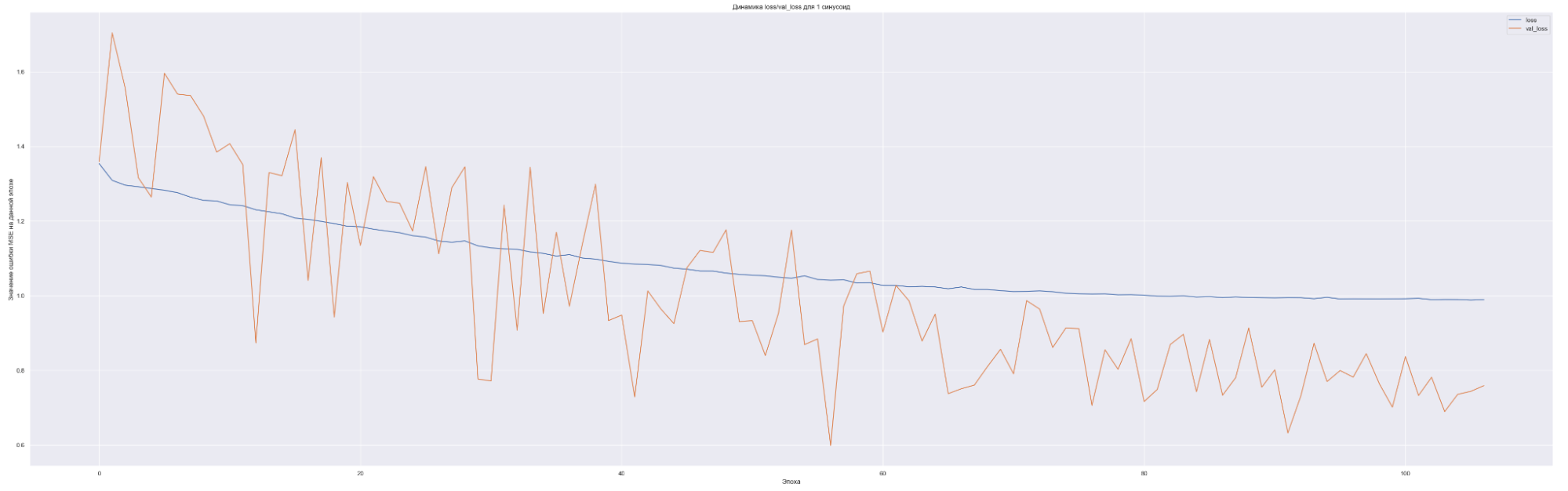
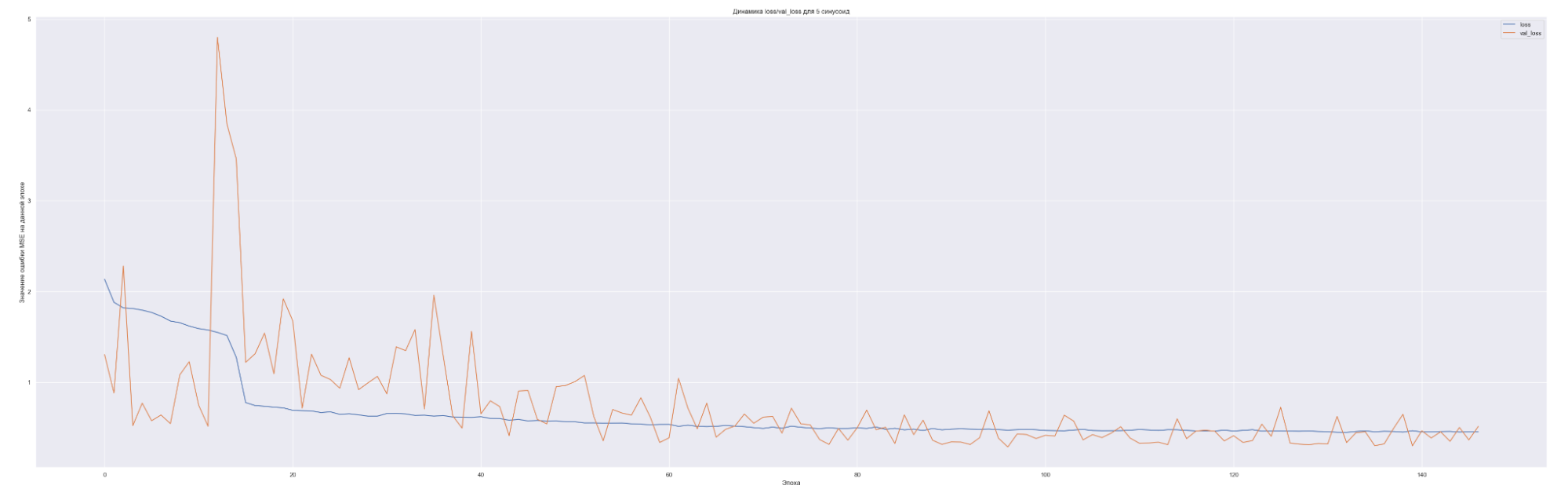
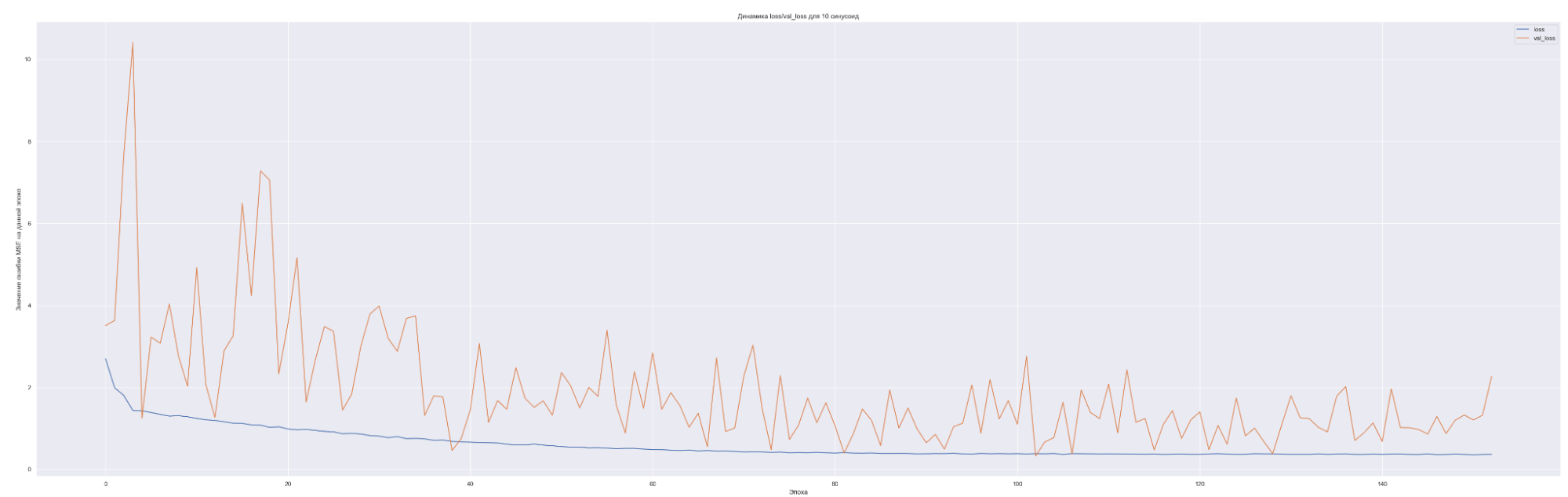
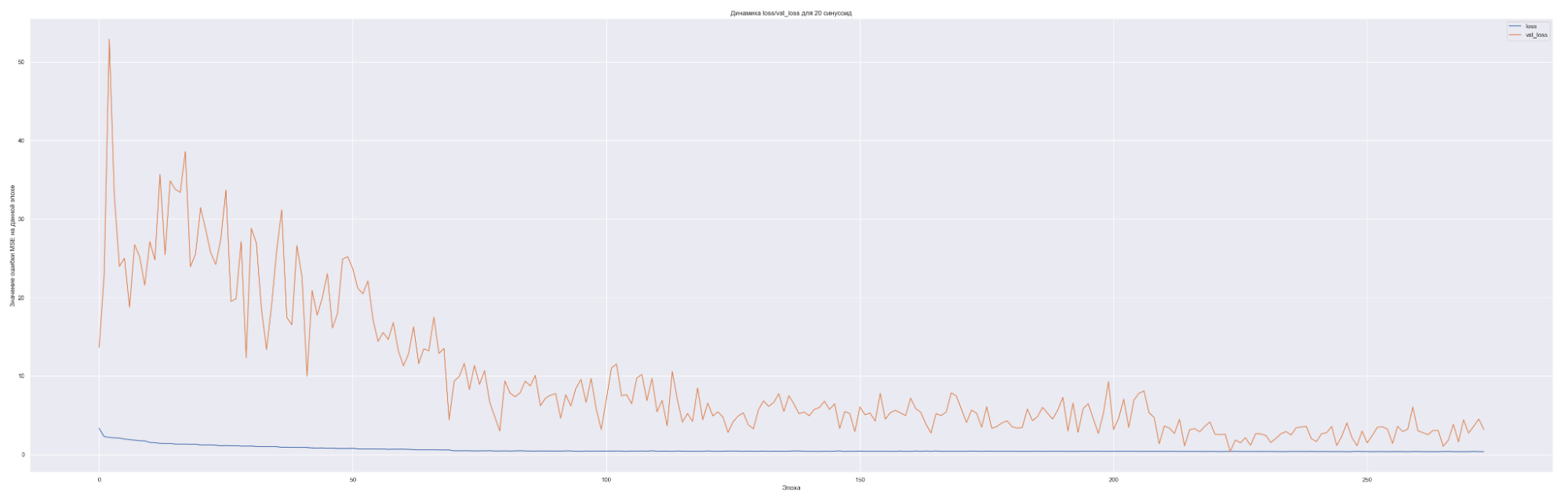
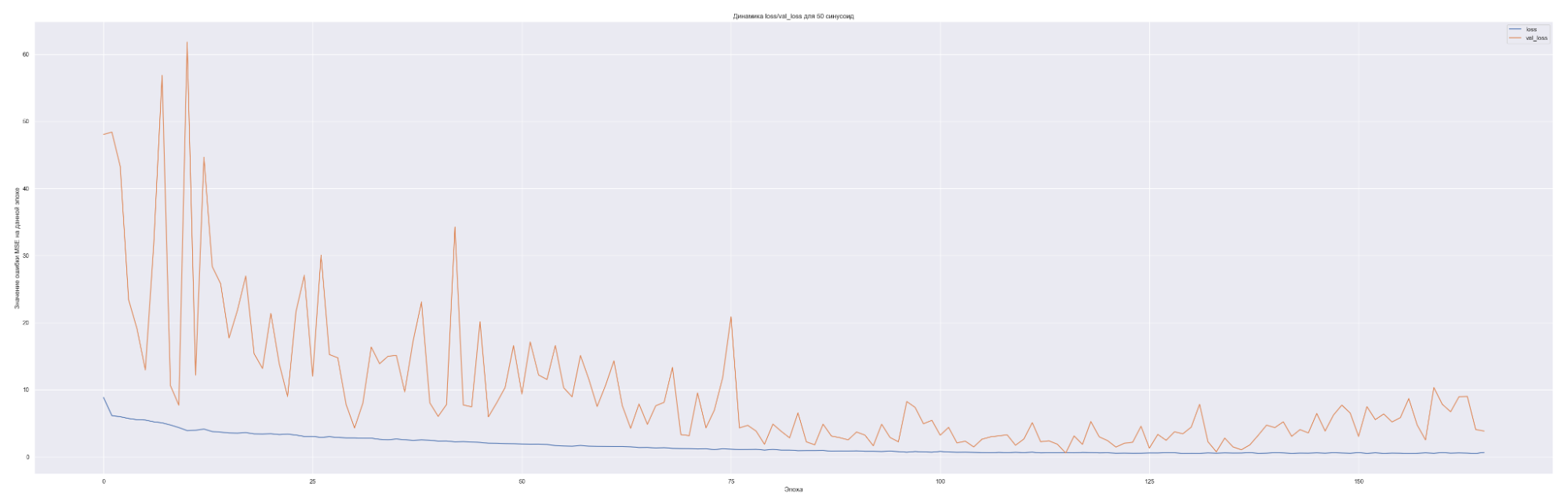
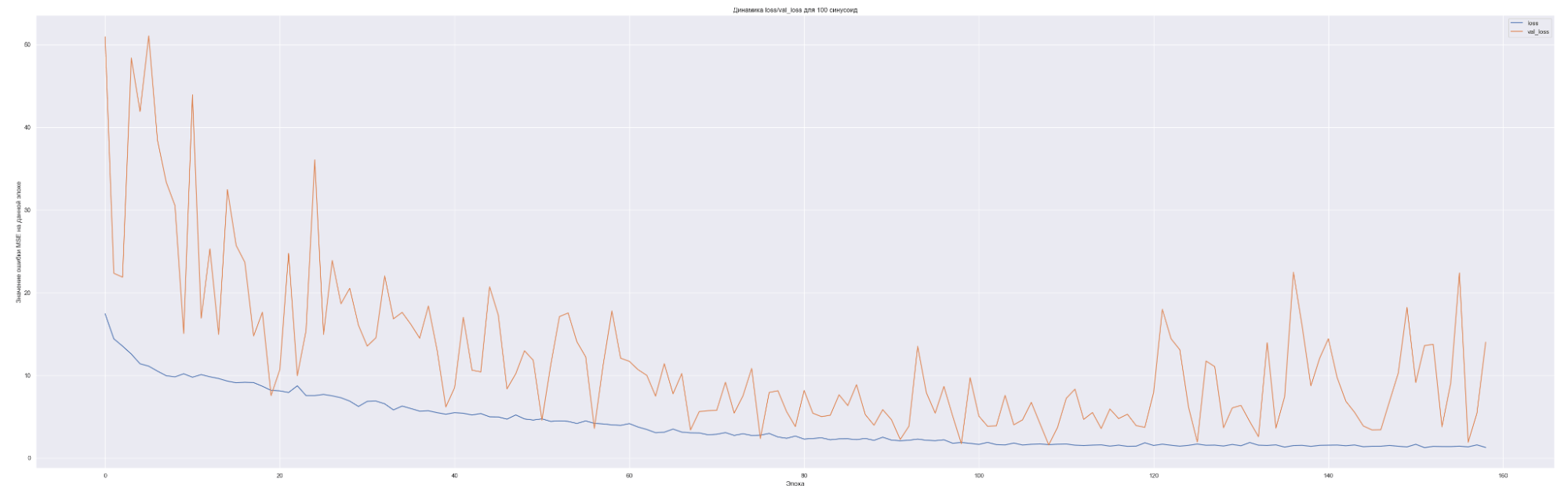
Посмотрим на динамику обучения нашей модели. Т. е. посмотрим, как меняется значение нашей невязки или loss-функции для каждой эпохи обучения:
| Количество синусоид | Минимальное значение loss-функции на данных валидации |
|---|---|
| 1 | 0.7 |
| 5 | 0.45 |
| 10 | 0.9 |
| 20 | 2 |
| 50 | 2 |
| 100 | 4 |
Что мы видим на данных графиках?
Чем больше количество синусоид, тем с большего значения начинает «работать» наша loss-функция на валидации (см. первые эпохи на графиках), т. е. более сложная модель ожидаемо сильнее переобучается. Но на последних эпохах loss-функция на данных валидации достаточно хорошо сходиться к loss-функции на тренировочных данных. Это говорит о том, что модель хорошо «улавливает» закономерности нашего временного ряда и что важно данные валидации хорошо коррелированы с тренировочными данными. Также можно заметить, что минимальное значение loss-функции, а именно 0.45 для пяти синусоид также соответствует минимальному значения MAE. Что естественно, т. к. чем меньше ошибка модели, тем лучше предсказательная способность модели. Не всегда, конечно, но чаще всего.
Важное замечание и вывод
Тут встает вопрос, почему даже со значительным увеличением количества суммируемых синусоид качество не повышается? Ответ на данный вопрос уже лежит в самом вопросе.
Вспомним, что представляет из себя наша loss-функция:
d = summa (a + summa (bj × sin (ωjt)) — y (t))2
Где j — это суммирование по количеству синусоид, а мы брали 1, 5, 10, 20, 50, 100 синусоид.
Нас сейчас интересует компонент summa (bj × sin (ωjt)).
Мы фактически производим расчет линейной комбинации синусоид, и здесь нет нелинейности, следовательно, данная функция не будет работать для сложных пространств, коим как раз и является наш временной ряд.
Помните что такое нейронная сеть?
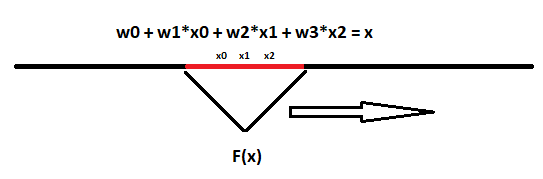
Однослойная нейронная сеть представляет из себя слой:
b0 + w0 × 0 + w1 × 1 + w2 × 2 + ... + wnxn = f (y) (в данном случае w — это веса нейронной сети).
Если функция преобразования f является просто линейной функций от аргумента (f(y) = y), то сколько аргументов нейронного слоя не делай, все равно это останется просто линейной комбинацией предикторов (функций от аргументов).
Хотя сами предикторы слоя могут быть и нелинейными. Например, так:
b0 + sin (ω0×0) + sin (ω1×1) + sin (ω2×2) + ... + sin (ωnxn) = y
Все равно их комбинация не будет иметь нелинейность.
Таким образом данный метод можно значительно улучшить введя нелинейность, но это уже совсем другой метод, который рассмотрим несколько позднее.
Качество предсказания достаточно посредственное. Наилучший результат получился для пяти синусоид. Метод для нашей задачи подходит не очень хорошо. Но мы используем этот метод для начального значения качества предсказания и остальные методы будем сравнивать с ним.
Ряд Фурье. Обратное преобразование Фурье. Матрица ожидания
Тут немного нужно разобраться в математике.
Пусть функция f (x) непрерывна на отрезке [a, b].
f (x) — это наша исследуемая функция.
Рассмотрим последовательность функций:
Данная последовательность функций является ортонормальной на [a, b] когда:
Обозначим:
Фактически мы нашу функцию разложили по ортонормированному базису набора функций (1), тогда ряд:
называется рядом Фурье. Где коэффициенты ak этого ряда называются коэффициентами Фурье функции f (x) по системе (1).
Если в качестве системы (1) взять ортонормированную на отрезке 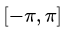 систему функций:
систему функций:
То разложение произвольной функции f (x) по системе (2) в ряд Фурье на отрезке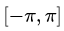 , имеет вид:
, имеет вид:
Где коэффициенты ak, bk имеют вид:
Ряд (3) называется тригонометрическим рядом Фурье. Ряды Фурье по другим системам называют обобщенными рядами Фурье. Далее мы будем подразумевать именно тригонометрический ряд Фурье.
Пусть дан временной ряд значений некоторого показателя:
При этом для значений последовательности (3) наблюдается определенная периодичность. Для исследования временного ряда (3) с постоянной периодичностью будем использовать тригонометрические ряды Фурье. В этом случае весь набор наблюдений s можно разбить на m периодов длины l +1, а массив измерений (3) можно представить в виде матрицы:
Размерности (l + 1) x m, в которой каждая строка:
является значениями показателя i-го периода (например, i-й недели).
Значения fit, t = 0, 1, 2, ..., l объявляются значениями некоторой функции fi (t), где аргумент:
Давайте функцию fi (t) заменим частной суммой тригонометрического ряда Фурье по косинусам:
Таким образом, получаем для каждого i-го периода частичную сумму ряда Фурье со своими коэффициентами:
для нахождения которых можно воспользоваться методом минимизации квадратичной ошибки:
Получаем систему уравнений для нахождения коэффициентов:
Количество слагаемых N в этом случае нужно выбирать не более длины периода l.
После того, как коэффициенты найдены, строится прогноз для следующего периода по формуле:
Примечание: здесь необходимо остановиться на применимости разложения в ряд Фурье нашего временного ряда.
Условия Дирихле сходимости ряда Фурье требуют, чтобы периодический сигнал заданный на отрезке удовлетворял следующим условиям:
- Сигнал не должен иметь бесконечных значений.
- Сигнал должен быть кусочно-непрерывным.
- Сигнал должен быть кусочно-монотонным и иметь конечное число экстремумов.
То есть в точках непрерывности ряд Фурье сходится к значению этих точек, а в точках разрыва первого рода к среднему арифметическому между левосторонним и правосторонним пределами.
Примечание: точка разрыва первого рода — это если скачок функции в точке имеет конечное значение.
- Первое требование удовлетворяется автоматически. Значения нашего ряда не имеет бесконечных значений. В нашей задаче сальдо по 62 счету не может быть бесконечным, хотя и может быть очень большим.
- Второе требование также выполняется, т. к. наш временной ряд непрерывный. Учитывается тот факт, что у нас временной ряд, т. е. ряд состоящий из значений отстоящих друг от друга на равные временные отрезки, причем для каждого временного отсчета значение временного ряда существует. Это мы гарантируем, т. к. сальдо 62 счета на каждый день не может быть «НеОпределено». Либо ноль, либо больше/меньше нуля, но конечное значение.
- Третье требование также выполнено, наш временной ряд кусочно-монотонный, и количество экстремумов конечно. Тут можно поспорить про монотонность. Т. к. наш ряд имеет сложную структуру — на одних участках возрастает, на других убывает. Но мы можем рассмотреть отрезки нашего временного ряда, где каждый из них будет вести себя монотонно. Можно удовлетворить этому условию более строго, если произвести сглаживание нашего временного ряда скользящим окном. Тогда достаточно легко выделить монотонные участки временного ряда.
Получится что-то примерно такое:
Моното́нная фу́нкция — функция одной переменной, определённая на некотором подмножестве действительных чисел, которая либо везде (на области своего определения) не убывает, либо везде не возрастает.
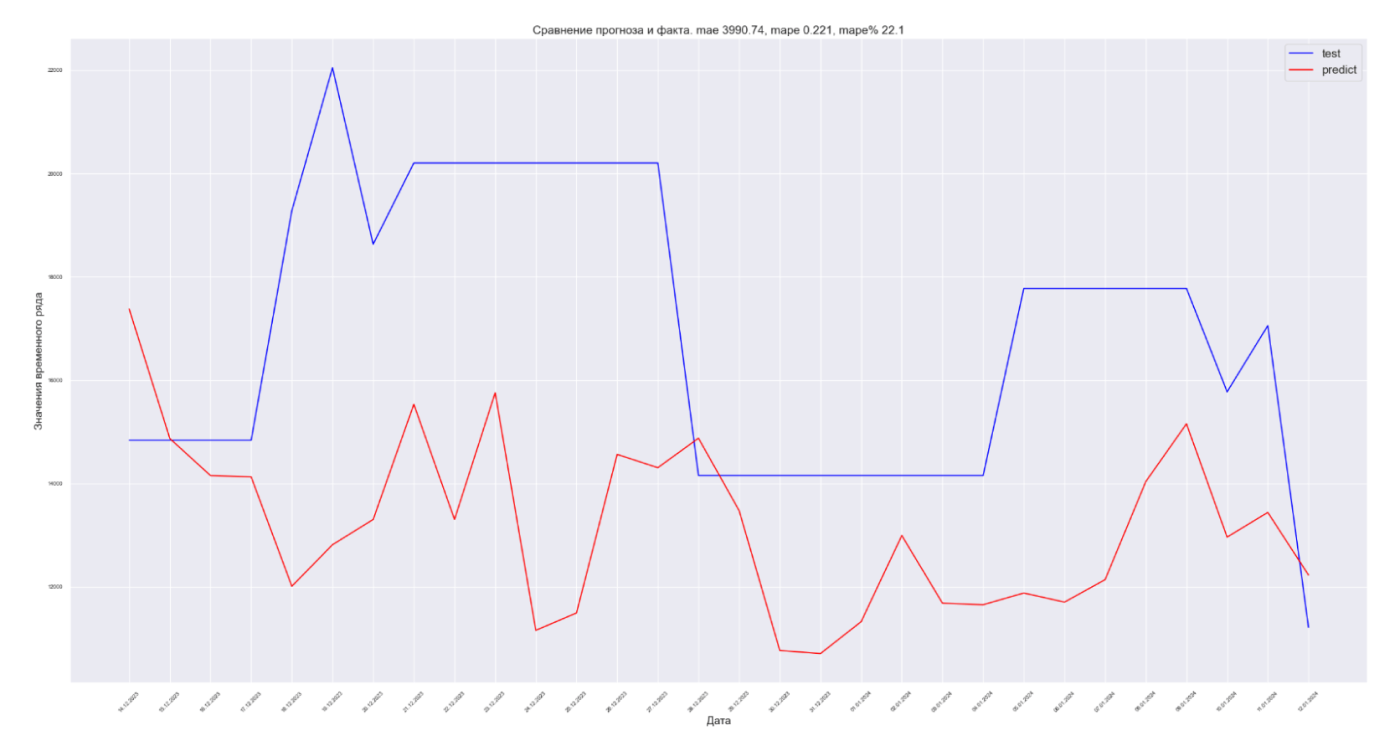
Примечание: здесь надо отметить, что для данного метода не имеет смысла приводить тренировочные данные на графике, т. к. не будет данных аппроксимации от модели. Модель строго говоря «работает» только на предсказание тестовых данных.
Получили MAE 3990.74.
Для данного временного ряда с помощью этого метода не получилось улучшить прогноз по сравнению с синусной подгонкой. Что-то надо придумать...
Возможные подходы к прогнозированию — удачная идея, которая сработала не сразу
Модель стековой нейронной сети
Раз простые модели не показали себя достаточными для адекватного моделирования нашей системы, давайте применим более «тяжелые» методы. Например, нейронные сети, а именно их разновидность — LSTM + полносвязная сеть.
Рассмотрим следующую структуру нейронной сети:
input → LSTM (100) → LSTM (100) → LSTM (100) → Dense (150) → Dropout (0.2) → Dense (30)
С оптимизатором Adam, а также с l2 — регуляризатором, с lambda = 0.0001.
Каждый семпл датасета содержит в себе 180 дней обучающих данных от n до n + 180 и 30 дней данных предсказания от n + 181 до n + 181 + 30. И так со смещением в один день вправо «нарабатываем» весь датасет.
Важно!
Разбиение датасета на тренировочный, валидационный и тестовый производим до нарезки на семплы, чтобы избежать «просачивания» данных валидации в тренировочные данные:
Причем следует отметить очень важную деталь — обучение нейросети будет у нас в два прохода. Сначала обучаем нейросеть на тренировочных данных и проверяем процесс обучения на данных валидации, чтобы не было эффекта переобучения. Когда обучение будет завершено, у нас будет известно количество эпох, которое потребовалось для обучения нейросети. Далее используя те же начальные веса нейросети, которыми была инициализирована нейросеть до обучения по первому проходу, мы опять производим обучение уже на датасете содержащем и тренировочные данные, и данные валидации. Количество эпох будет равно вычисленному на первом проходе.
При таком подходе наша нейросеть, естественно при допущении, что данные валидации из той же генеральной выборки, что и тренировочные данные, будет обучена и на очень важном куске датасета, который ближе к актуальным датам тестовой выборки.
Также перед обучением датасет подвергался нормализации путем вычитания среднего и деления на стандартное отклонение. Среднее и стандартное для первого прохода отклонение вычислялось только по тренировочной выборке, а затем применялось и для тренировочного датасета, и для датасета валидации.
Результат обучения модели:
Получили MAE 1949.
Уже лучше. Данная идея позволила значительно улучшить предсказательный результат модели по сравнению с моделированием синусом. 1949 против 2152 для моделирования синусом.
Гибридная нейросеть: Сверточная НС + Стековая НС = неполная удача
Давайте попробуем усложнить нашу нейросеть. Ведь фактически в LSTM мы передавали просто сегмент — набор точек.
Теперь давайте использует ту же идею, что и при обработке изображения, а именно свертку. Только если при обработке изображений свертке подвергается двумерная структура, то при обработке временного ряда будем использовать одномерную свертку.
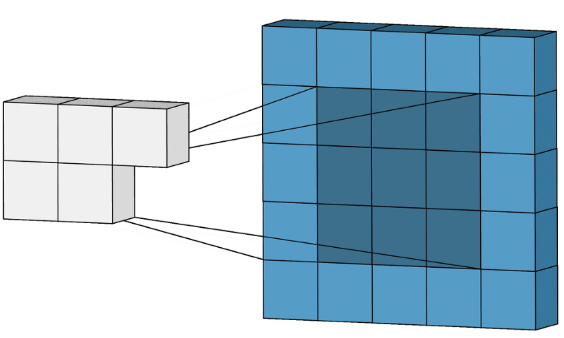
Принцип двумерной свертки — это когда есть матрица N × N, и наша программа «умножает» эту матрицу в каждой позиции изображения, потом суммирует это в одно значение и вычисляет от этого значения некоторую, часто нелинейную функцию — relu, sigmoid, или tanh. И далее смещает позицию применения этой матрицы сверху → вниз и слева → направо.
В одномерной свертке все точно также, только размер сверточного ядра равен просто N.
В результате мы добьемся того эффекта, что каждая точка датасета будет в себе агрегировать данные по соседним точкам, что должно положительно сказаться на качестве работы модели.
Примечание: почему это работает? При работе с изображениями, чем точки изображения ближе друг к другу, тем они чаще всего более похожи друг на друга, по таким параметрам как яркость, цвет. И только в тех местах, где яркость меняется сильно, говорят, что градиент претерпевает сильные изменения — близкие точки сильно отличаются между собой по значению яркости.
Следовательно, применяя фильтр к изображению, мы заставляем нейросеть выделять некоторые признаки — линии, углы и прочие примитивы изображения. Также и применяя одномерные фильтры к значениям временного ряда мы заставляем нейросеть выделять «примитивы» временного ряда более высокого порядка, нежели просто значение временного ряда в одном временного отрезке.
Имеем такую нейросеть:
input → Conv1D (64) → Conv1D (128) → Conv1D (256) → LSTM (100) → LSTM (100) → LSTM (100) → Dense (150) → Dropout (0.2) → Dense (30)
С оптимизатором Adam, а также с l2 — регуляризатором, с lambda = 0.0001.
Режим формирования датасета останется таким же.
Результаты обучения:
Получаем MAE 1831.
Стало еще лучше! 1831 против 2152 для моделирования синусом, 1949 для простой LSTM-стековой нейронной сети.
Но все равно... Нет предела совершенству! Может поработаем с данными?
Изменение подхода к подготовке ряда. Собираем все вместе
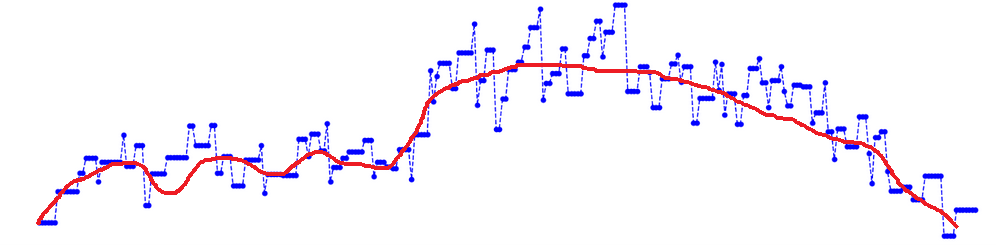
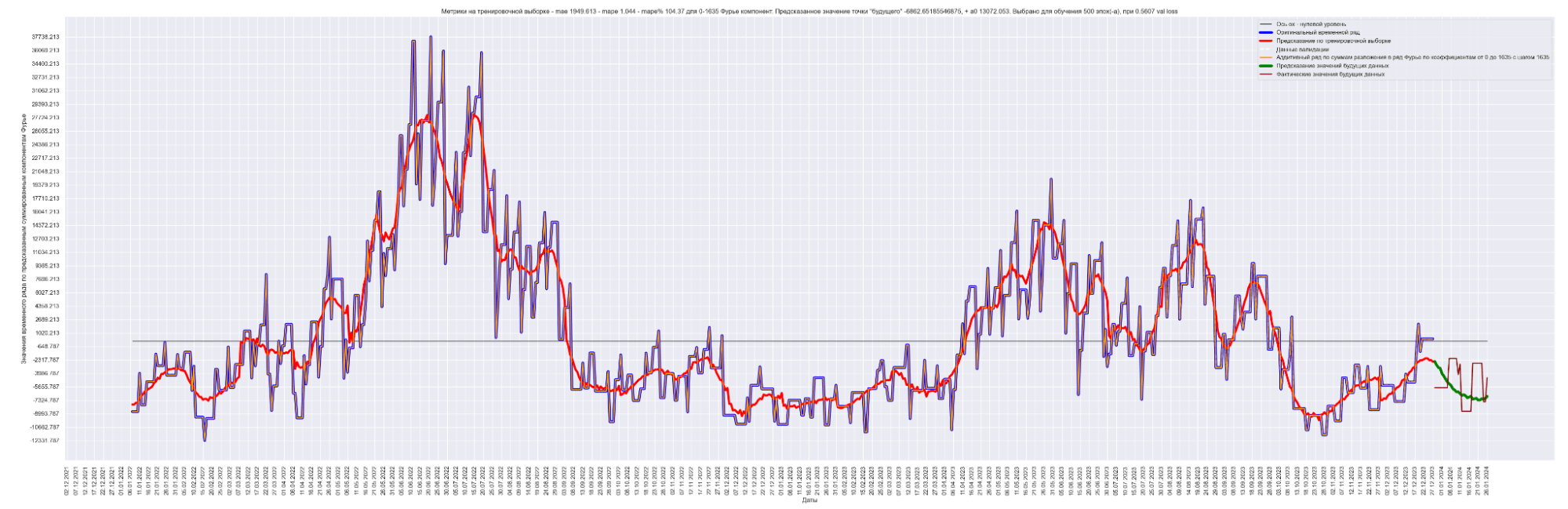
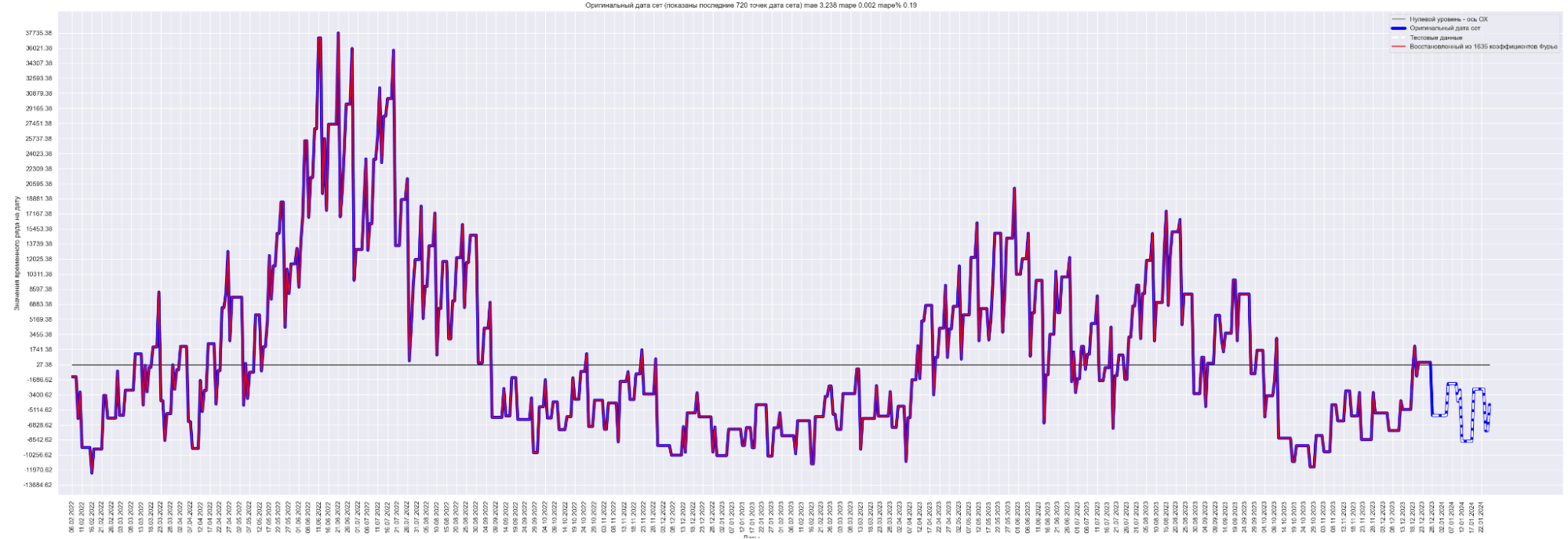
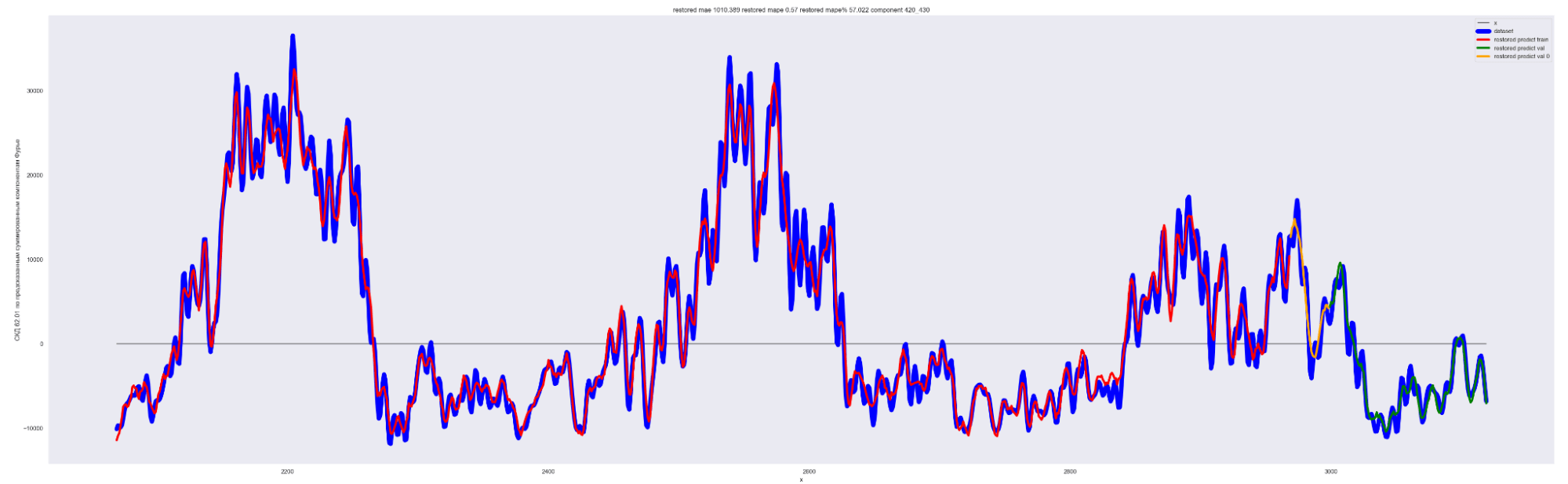
Давайте посмотрим на наш временной ряд и временной ряд, восстановленный из полученных коэффициентов Фурье:
Синим выведен оригинальный временной ряд.
Красным — восстановленный из 1635 коэффициентов Фурье временной ряд.
Видно, что восстановленный временной ряд с точностью до MAPE% = 0.19 соответствует оригинальному временному ряду.
Это ожидаемо и правильно.
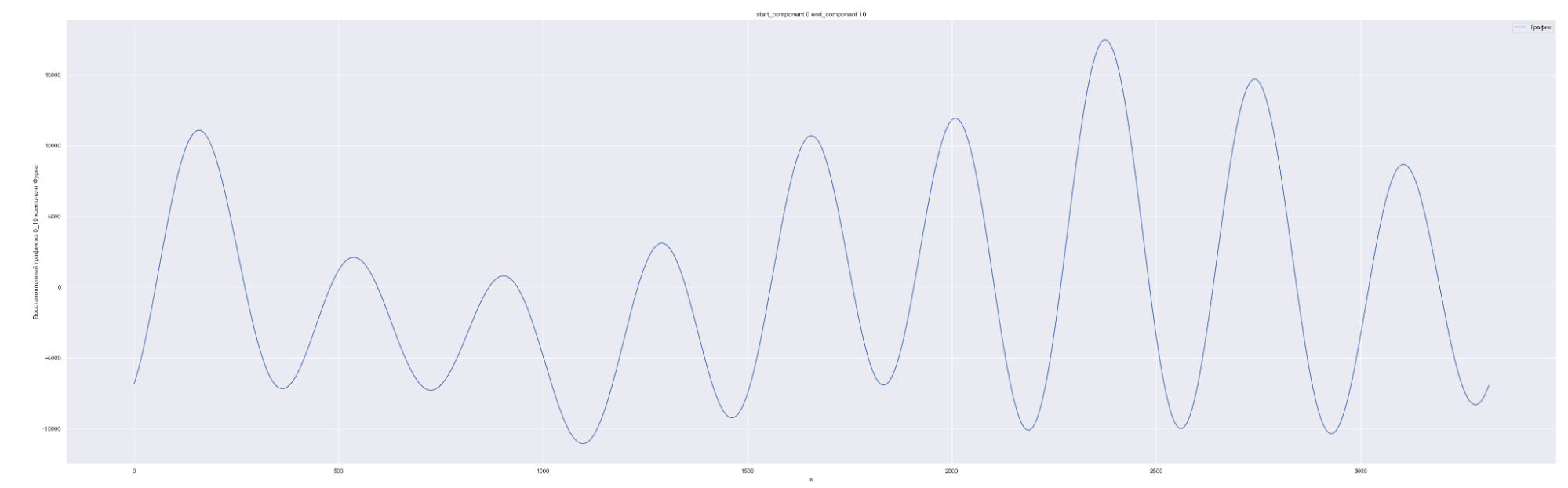
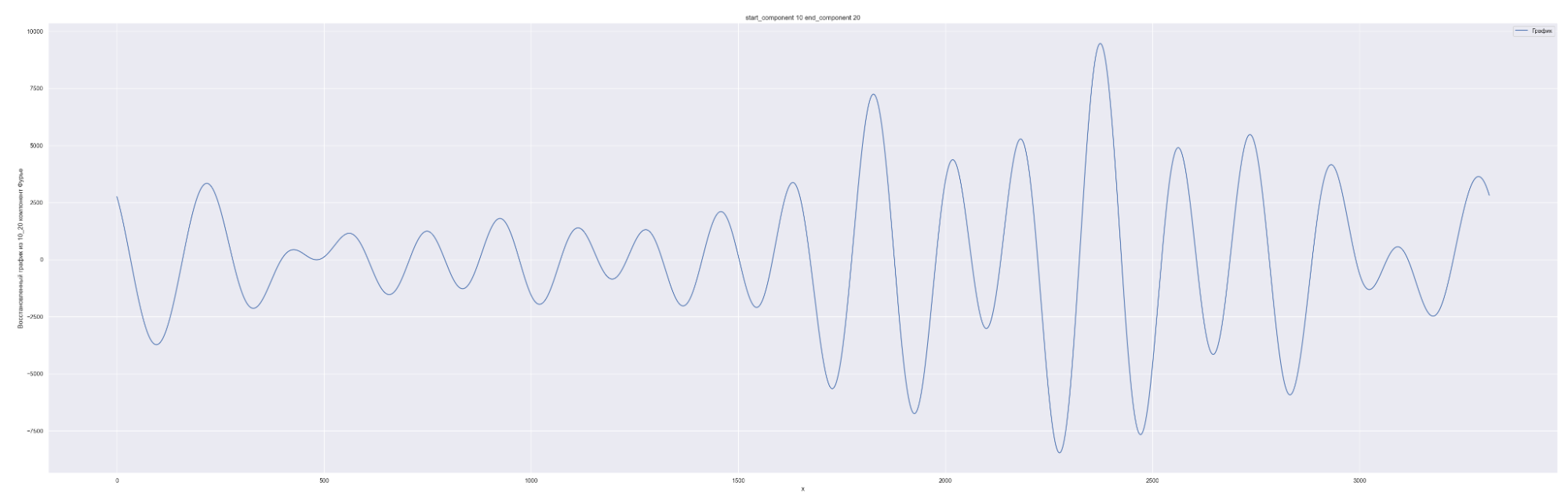
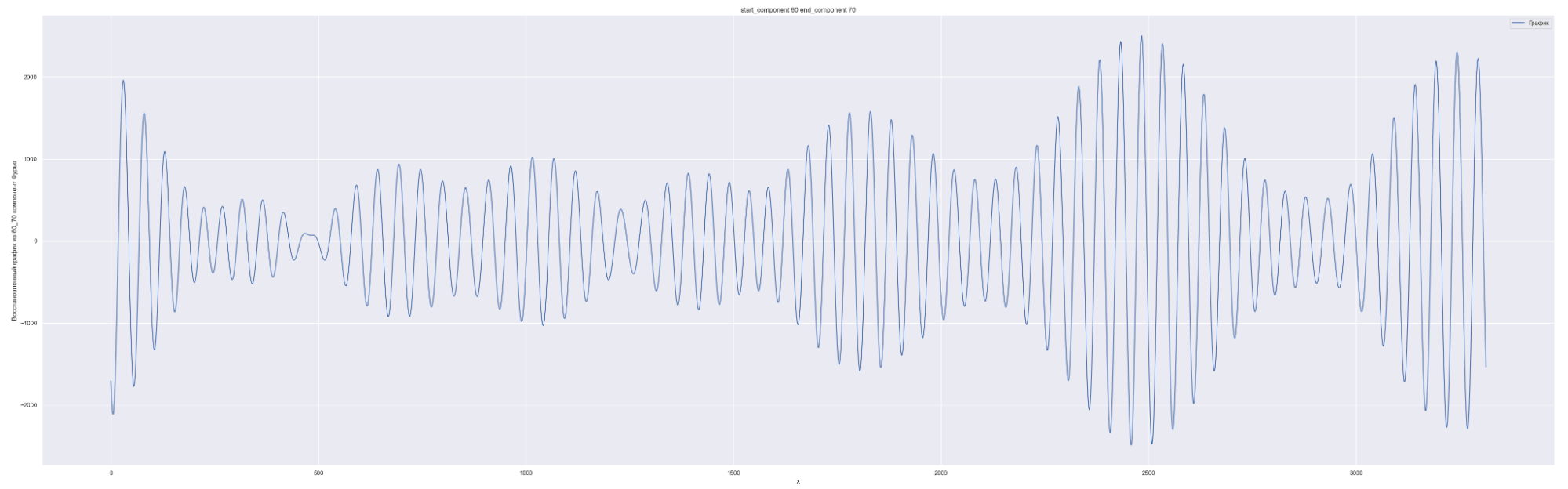
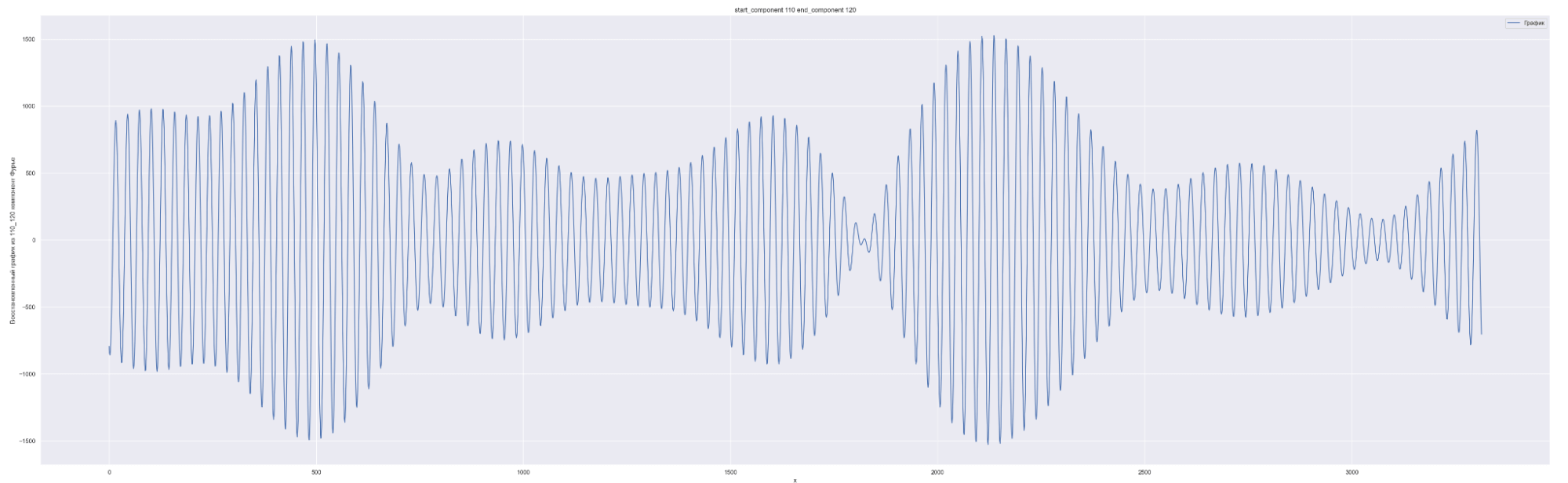
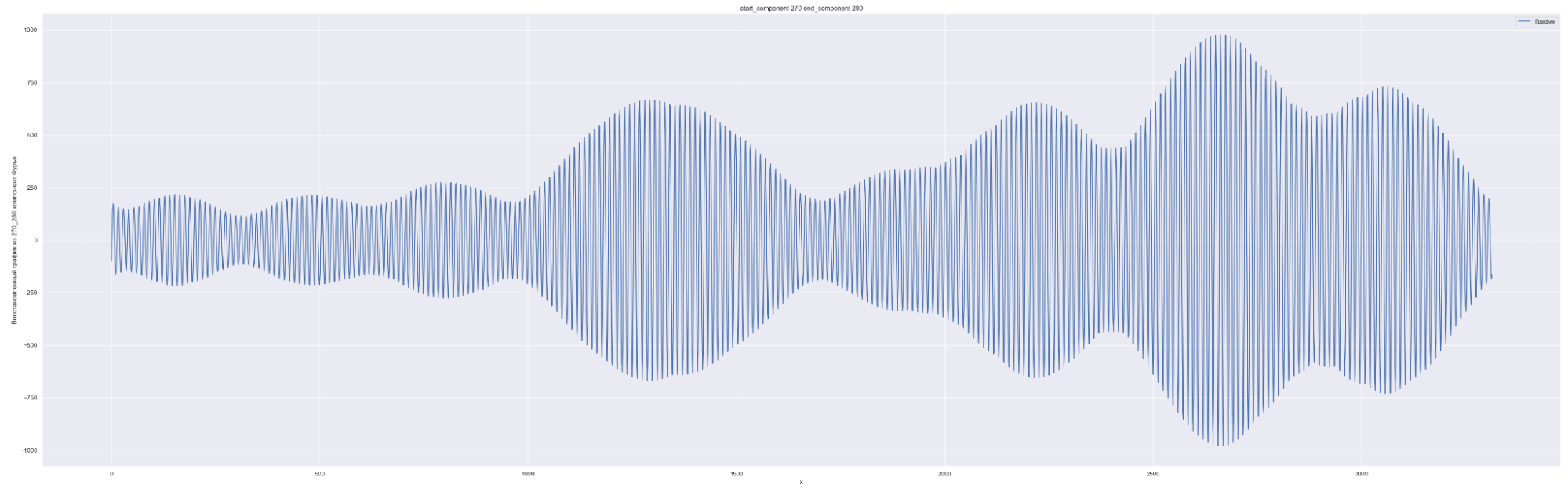
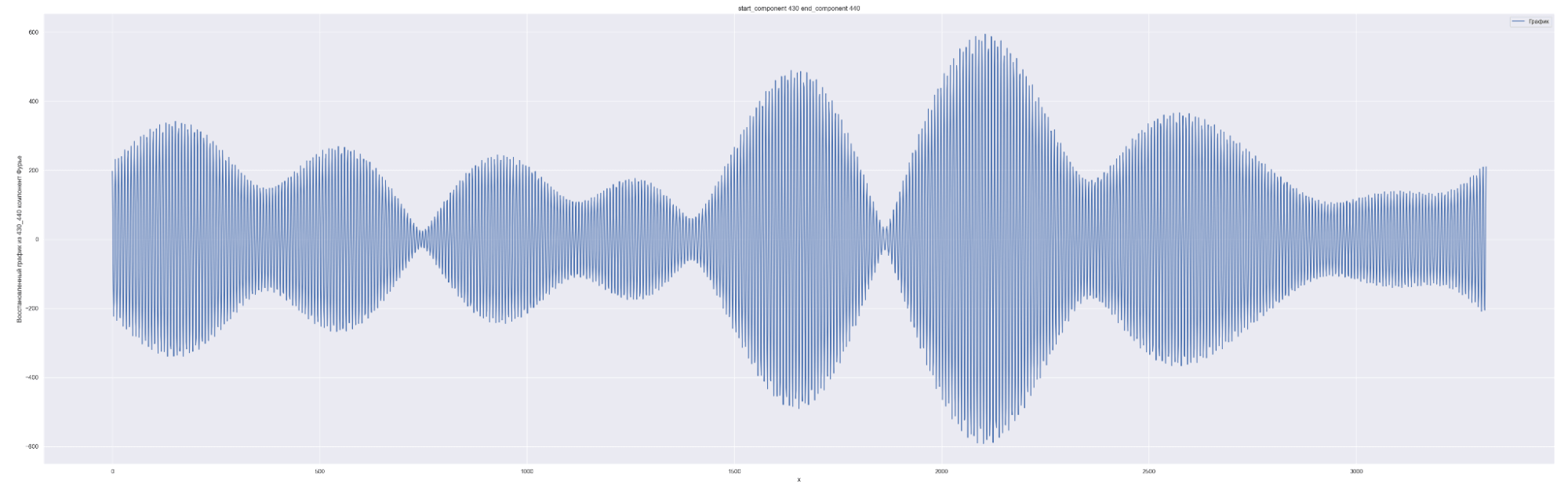
Разложим наш временной ряд в ряд Фурье с разным количеством коэффициентов Фурье — от 0 до 1635, с шагом в 10.
1635 равно половине длины временного ряда. Приведены несколько скринов разложения.
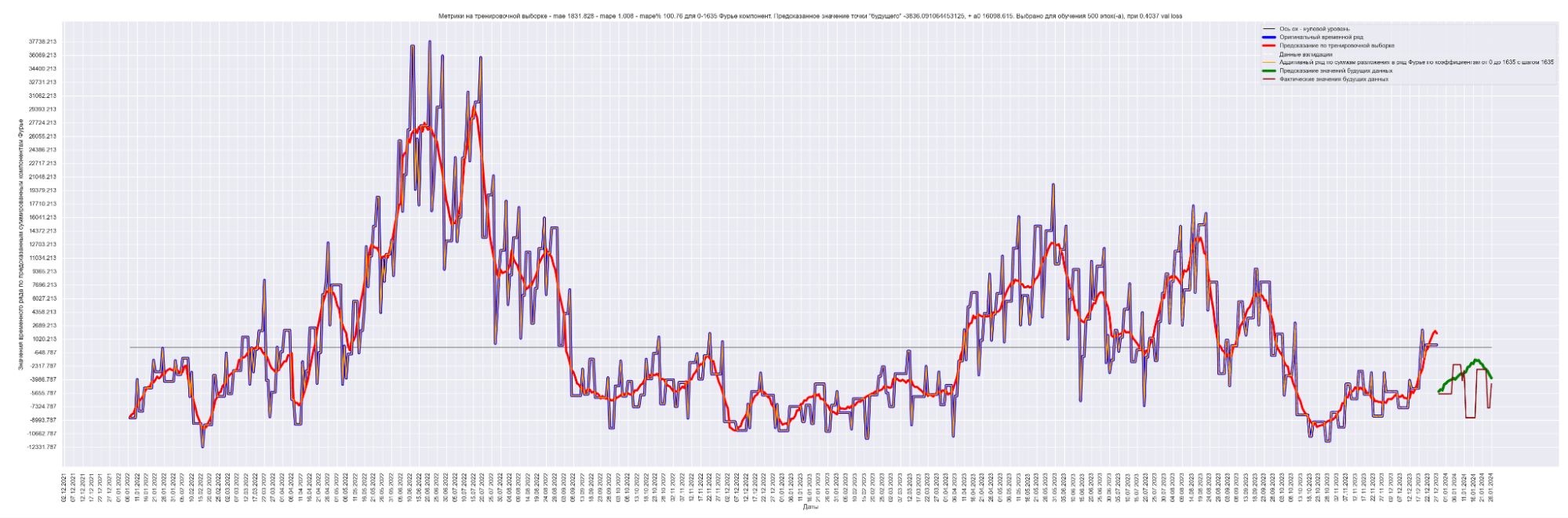
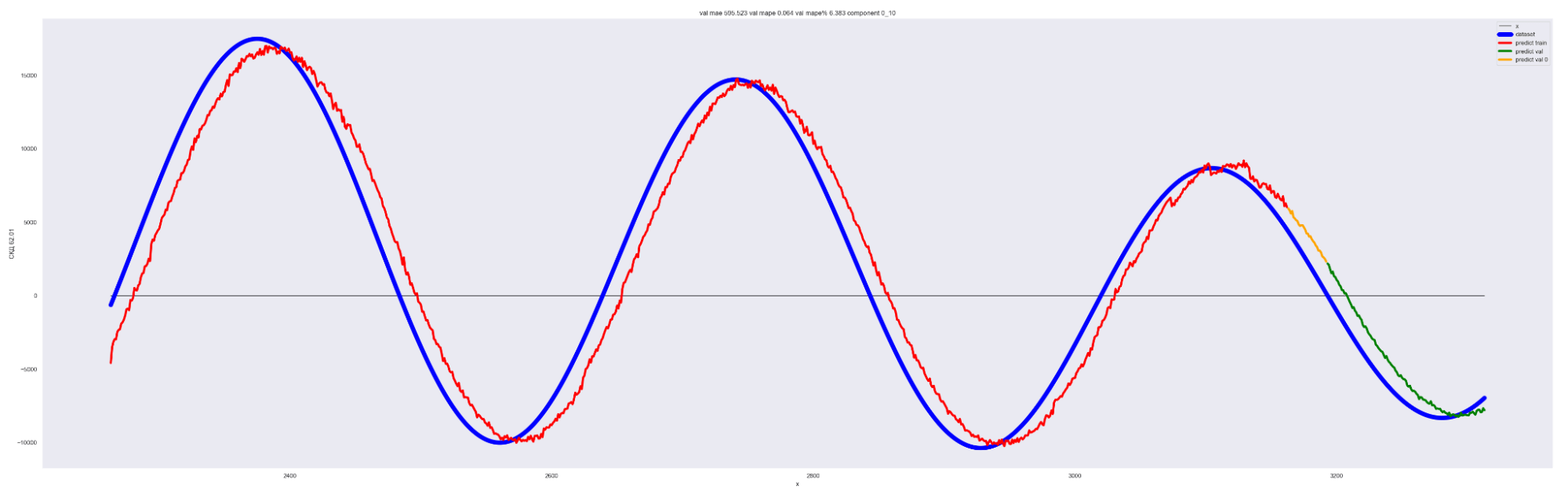
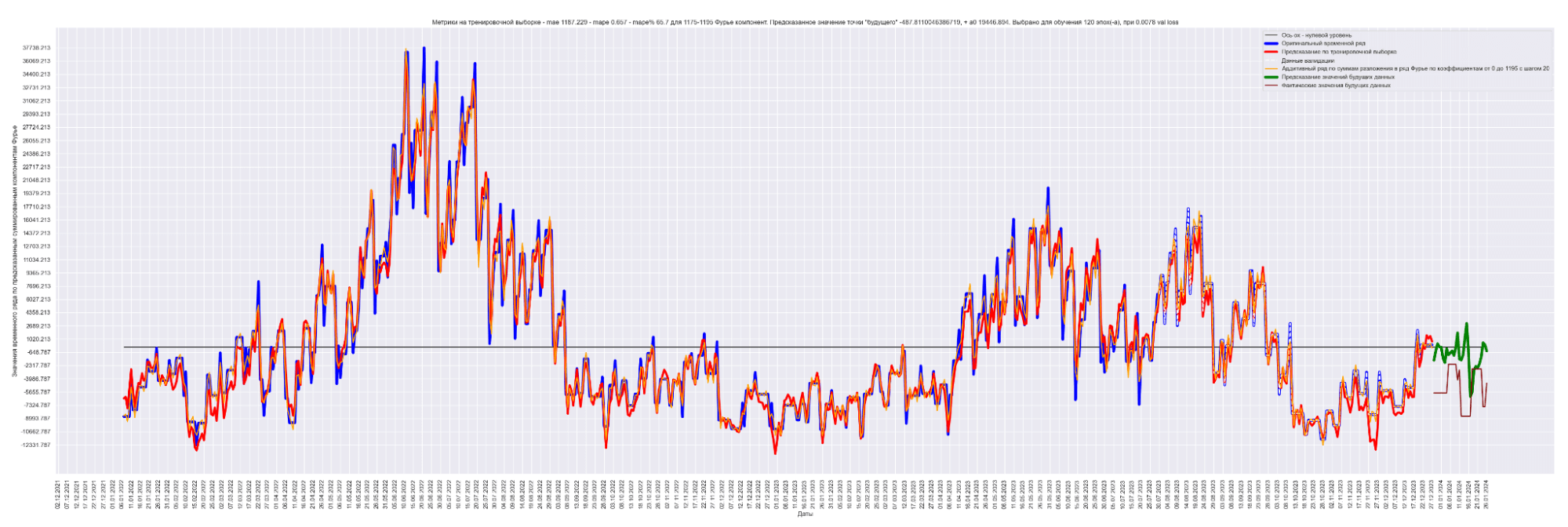
А теперь попробуем обучить нейронную сеть на всех разложениях в ряд Фурье:
То есть наша модель хорошо подгоняется к ряду, разложенному по коэффициентам Фурье.
Красная линия — прогнозное значение на тренировочных данных.
Оранжевая линия — прогнозное значение на данных валидации.
Зеленая линия — прогнозное значение на тестовых данных.
Синяя линия — данные нашего временного ряда.
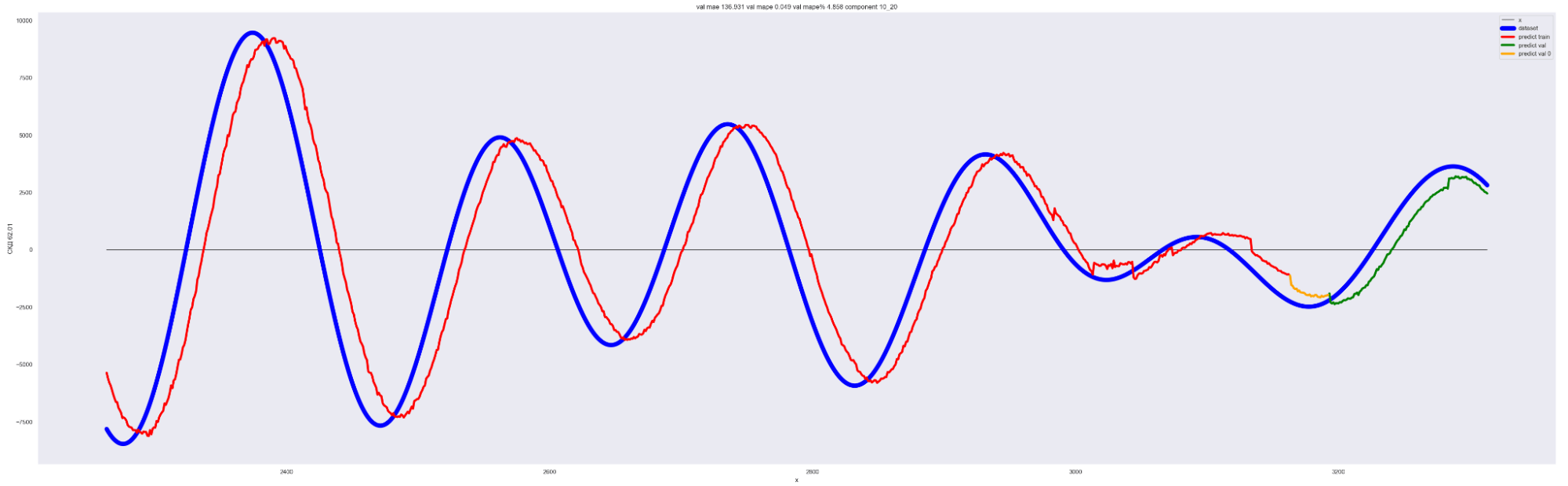
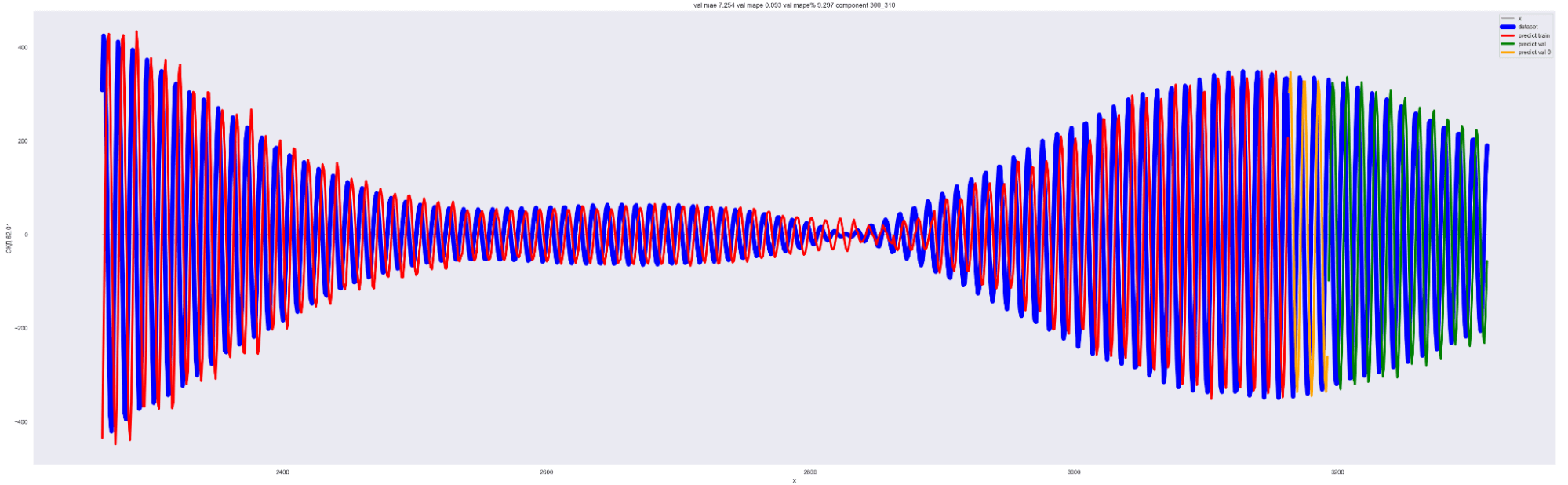
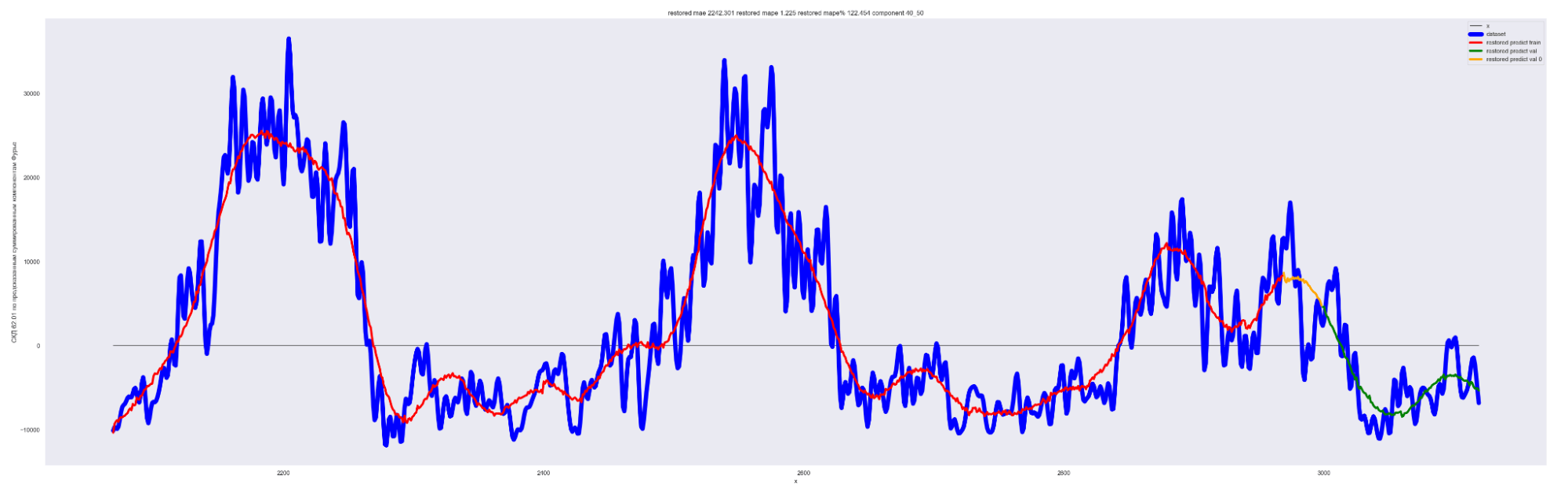
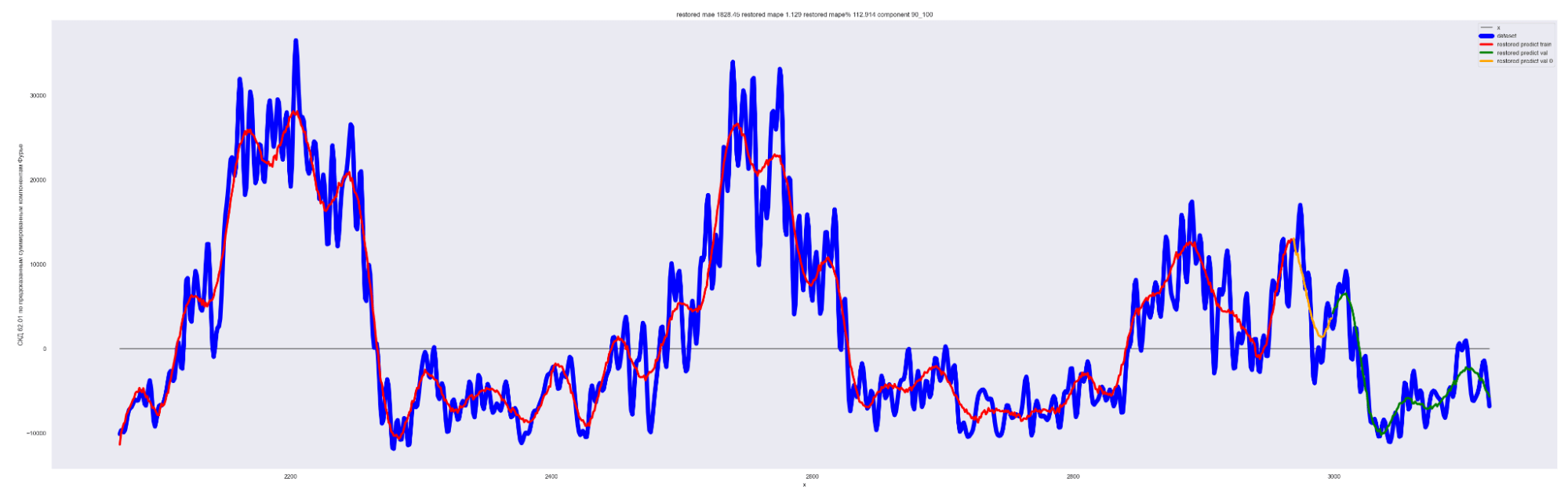
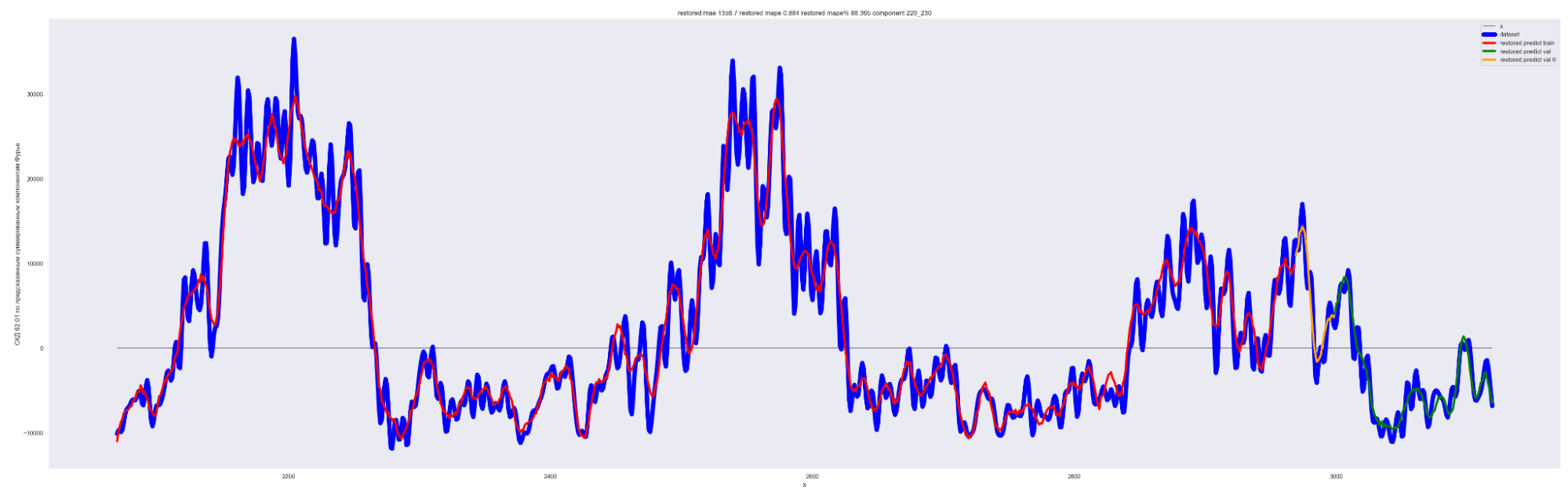
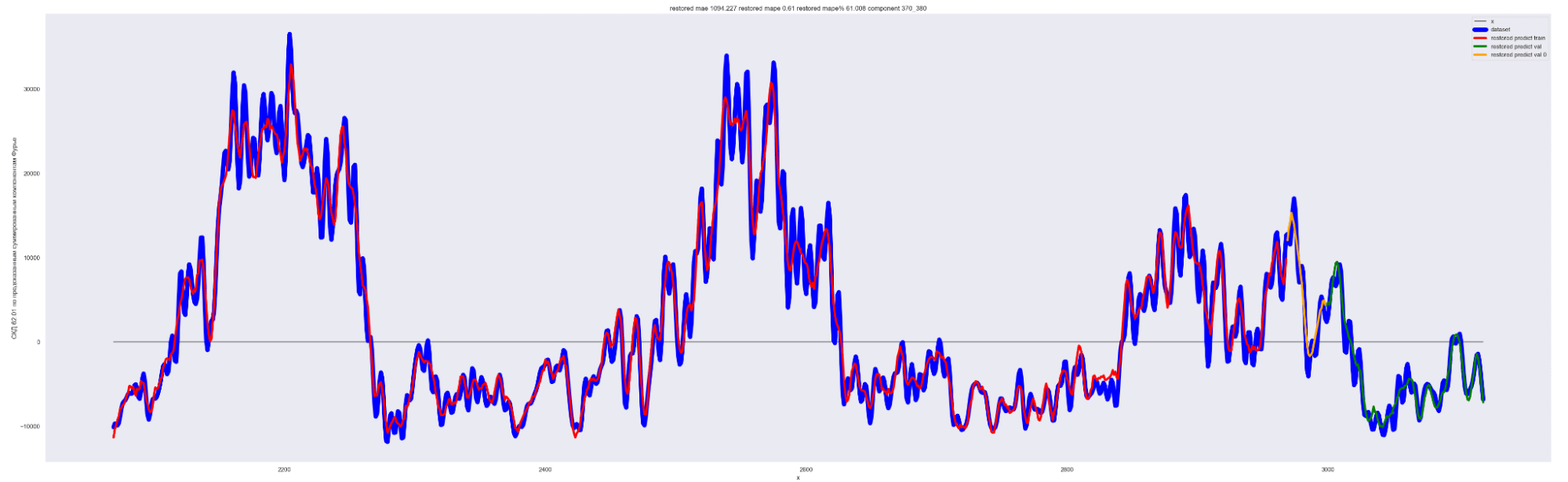
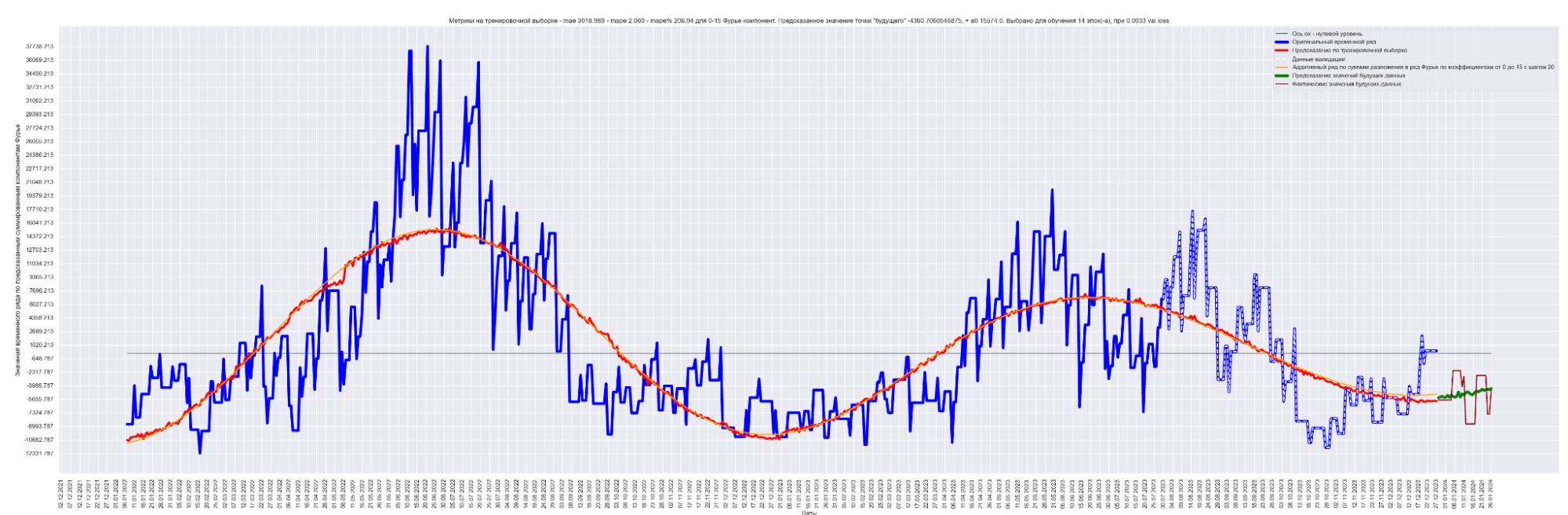
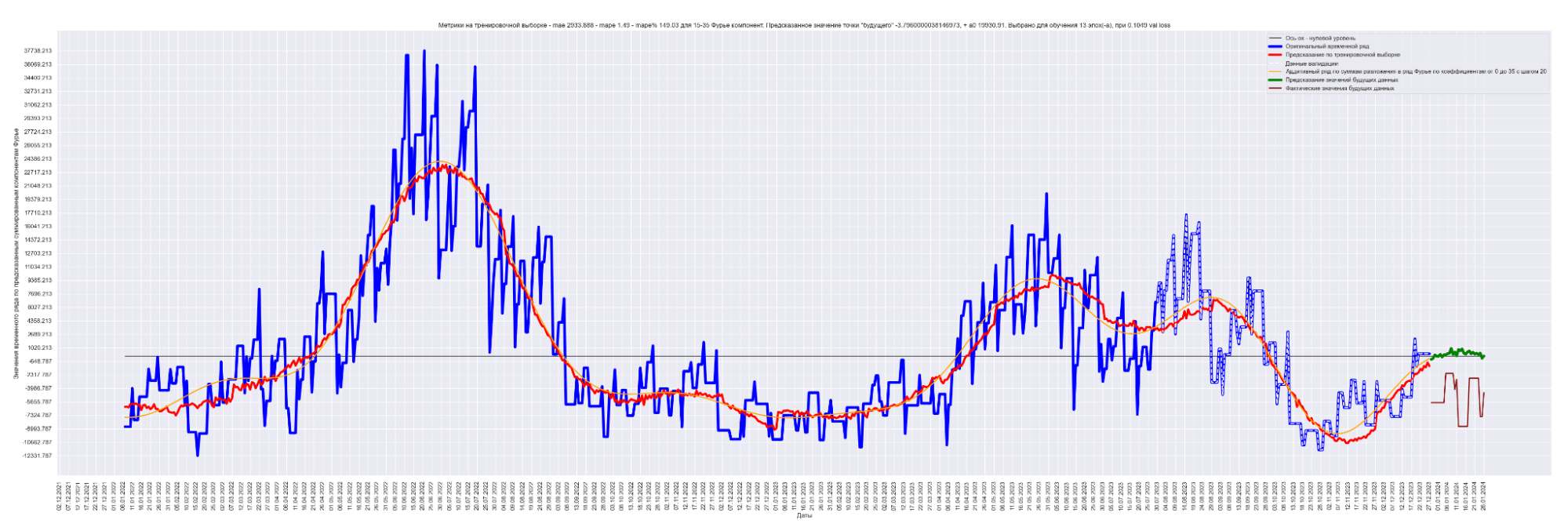
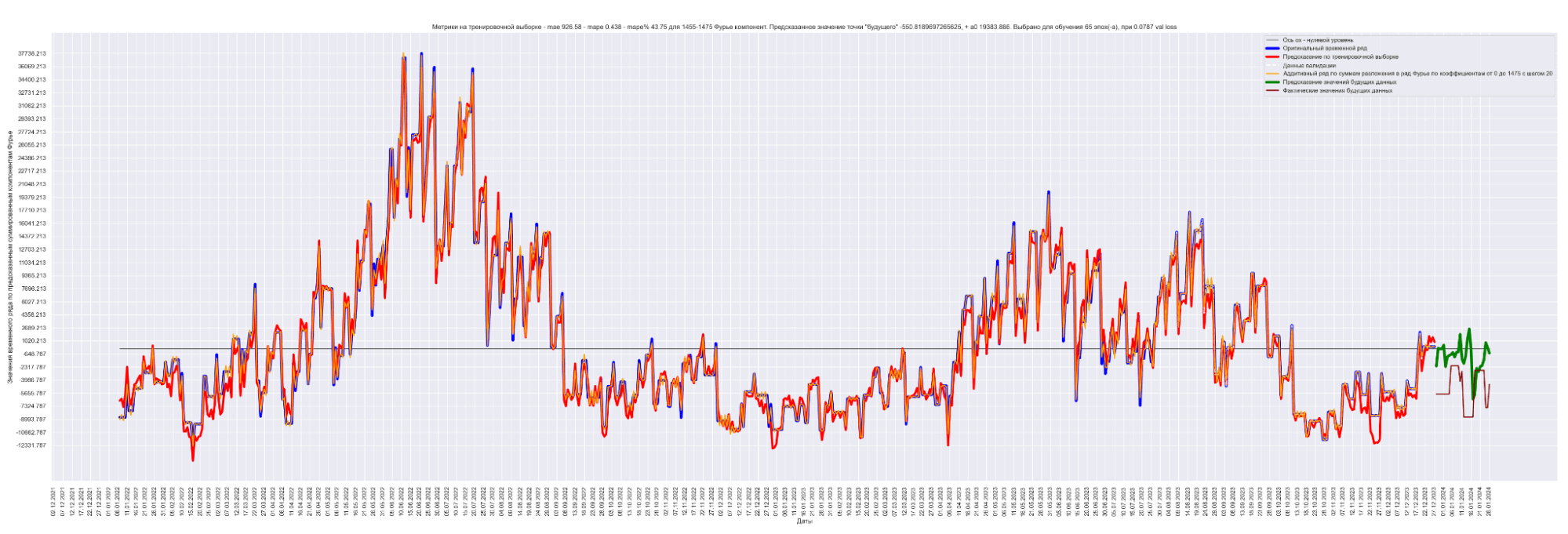
А теперь проделаем тоже самое, но будем каждый следующий разложенный временной ряд суммировать с разложенным временным рядом на предыдущем разбиении, также выведем предсказания для соответствующей модели. И сделаем вывод графиков:
Мы можем применить эту идею — возьмем наш временной ряд длиной L, разобьем на интервалы с шагом в 20 для L/2 длины ряда. Для каждого такого интервала произведем разложение в ряд Фурье, произведем обучение отдельной модели для каждого разложения и получим (L / 2) / 20 моделей.
Далее, чтобы произвести предсказание будущих точек для каждой модели и приближение модели для тренировочных данных, данных валидации, сделаем предсказание по разложенному в ряд Фурье. Затем результаты предсказания от каждой модели в каждом конкретном дне сложим. В результате получим значения предсказанного временного ряда.
То есть каждый член ряда призван сделать свою часть прогноза для каждого конкретного дня. Это основная идея этого метода.
Примечание: шаг разбиения 20 выбран экспериментально. Это подбираемый гиперпараметр модели. Чем он меньше, тем лучше будет модель аппроксимировать восстановленный график. Но и тем больше получится моделей. Нужно находить баланс между прогнозным качеством модели и скоростью обучения общей модели.
Очень интересная технология получается, когда шаг является переменным. Можно заметить, что при небольших значениях коэффициента Фурье (~1-50) возможно шаг сделать больше, а далее его уменьшать. Но все равно это тема для отдельного исследования. Мы же сейчас здесь примем шаг постоянный.
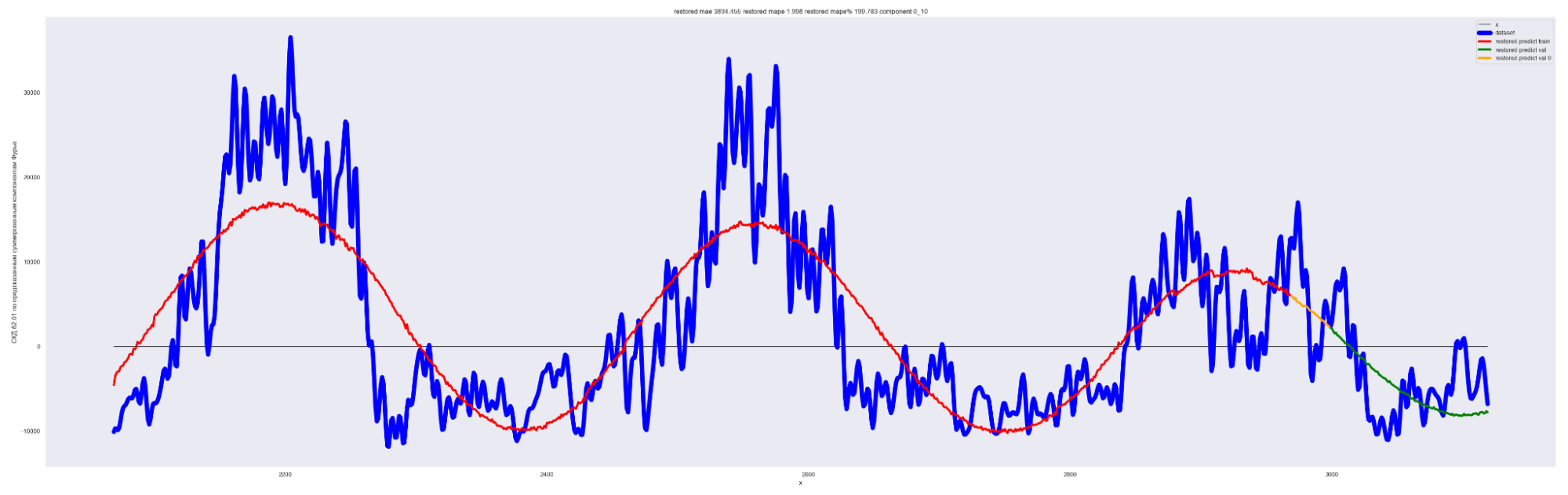
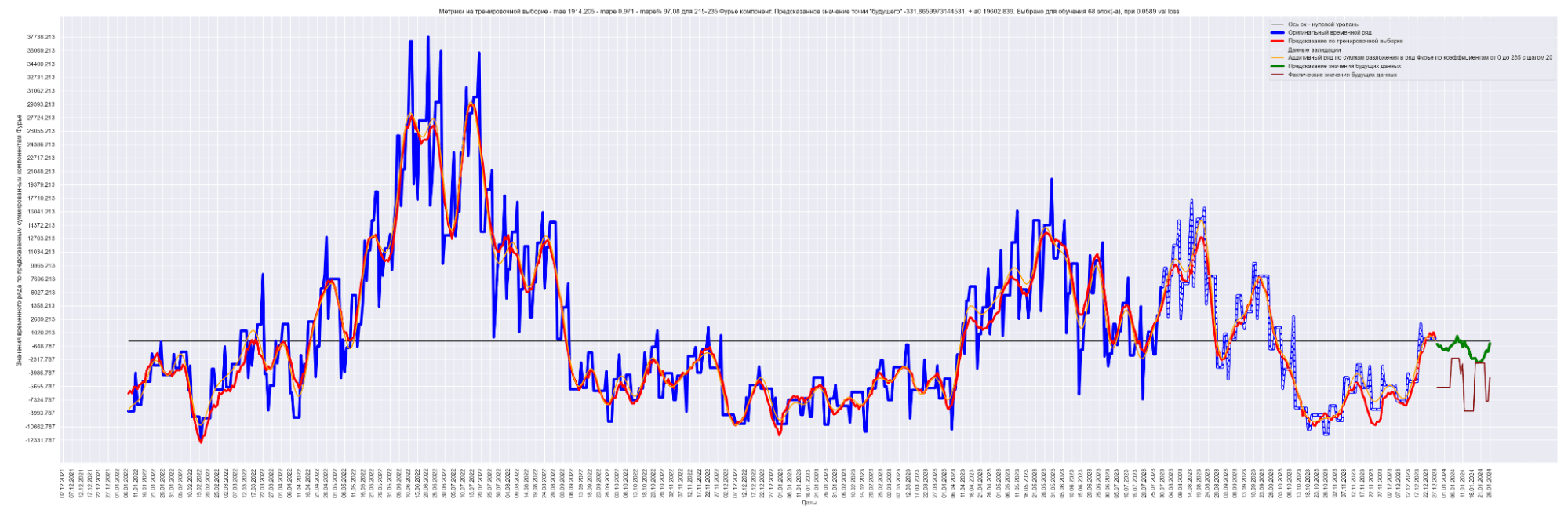
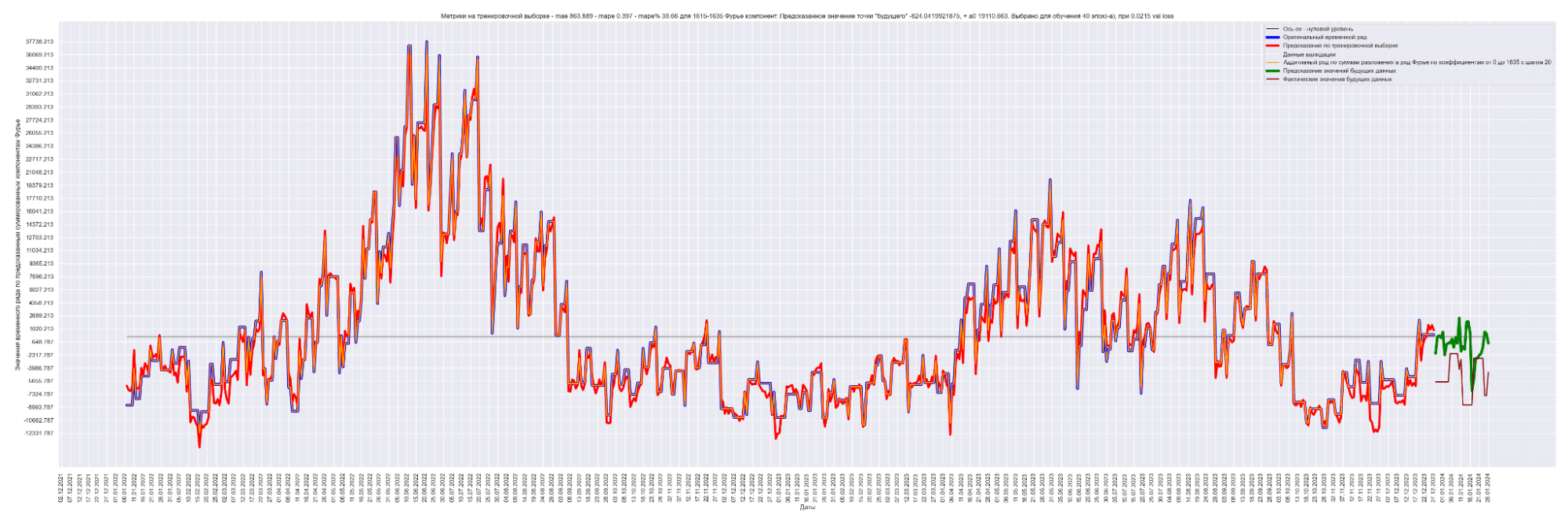
Результат обучения M моделей. Шаг разбиения применялся равным 20:
Получаем MAE 863.
Уже намного лучше! 863 против 2152 для моделирования синусом, 1949 для простой LSTM-стековой нейронной сети и 1831 для сверточной + LSTM-стековой нейронной сети.
Конечно, и этот результат можно значительно улучшить применением ансамблевых моделей — обучить несколько моделей с немного разной структурой, а результат предсказания усреднить, тогда ошибка будет еще меньше.
Сводная таблица сравнения результатов:
| Модель | MAE |
|---|---|
| Моделирование синусом | 2152 |
| Простая LSTM-стековая нейронная сеть | 1949 |
| Гибридная сеть — сверточная нейронная сеть + LSTM-стековая нейронная сеть | 1831 |
| Гибридная сеть — сверточная нейронная сеть + LSTM-стековая нейронная сеть + разложение по коэффициентам Фурье с суммируемым результатом | 863 |
Таким образом приведенная модель с дополнительной предобработкой данных позволила — 863 / 2152 = 0.401 — более, чем на сорок процентов улучшить качество работы модели относительно базовой модели. Это довольно хороший плюсик. :)
Выводы
Мы провели интересную работу по прогнозированию фактических продаж и оплат для клиента с горизонтом прогноза в тридцать дней. Сам горизонт прогнозирования является крайне важным гиперпараметром при построении и обучении модели для прогноза, так как если горизонт прогноза мал, то возможно применение менее «тяжелых» моделей и алгоритмов. При увеличении горизонта прогноза модели сложнее произвести корректное предсказание, потому что энтропия (неопределенность) событий с ростом дня предсказания увеличивается. Потребуется введение более сложных моделей, что ставит перед исследователем ряд таких вопросов, как стабилизации обучения, переобучения модели и прочие.
Но нас ничто не должно останавливать! Хоть прогнозирование временных рядов — это примерно то же самое, что ехать на машине, смотреть только на зеркало заднего вида и пытаться предсказать, что у нас там впереди... Но все же это лучше, чем ехать с закрытыми глазами. Если мы видим, что в зеркале заднего вида дорога уходит вправо, то скорее всего и впереди дорога также уходит вправо. Здесь только можно пожелать, чтобы этот изгиб дороги был не очень сильным, иначе мы не успеем увидеть начало изгиба дороги в зеркале заднего вида, и мы уже в кювете. :)
Отсюда вывод: при прогнозе временных рядов желательно, чтобы изменения временного ряда были как можно более плавными в определенных пределах.
От экспертов «1С-Рарус»














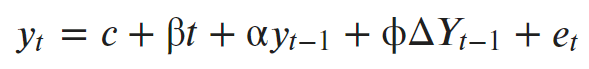
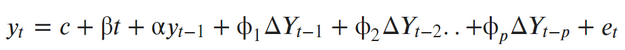
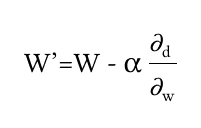
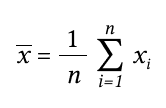
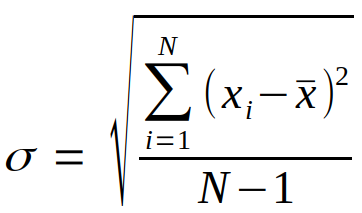
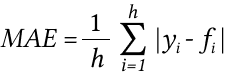
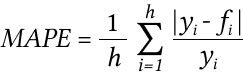

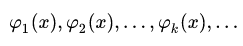 (1)
(1)
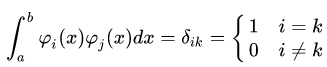
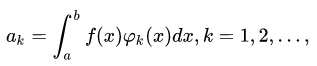
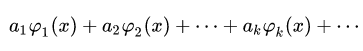
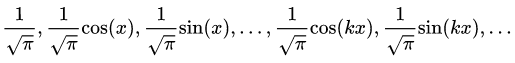 (2)
(2)
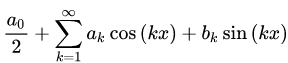
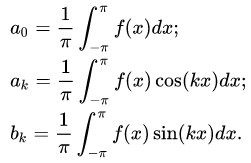
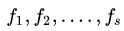 (3)
(3)
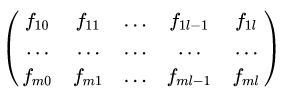 (4)
(4)